Stage-Aware Learning for Dynamic Treatments

Recent advances in dynamic treatment regimes (DTRs) provide powerful optimal treatment searching algorithms, which are tailored to individuals' specific needs and able to maximize their expected clinical benefits. However, existing algorithms could suffer from insufficient sample size under optimal treatments, especially for chronic diseases involving long stages of decision-making. To address these challenges, we propose a novel individualized learning method which estimates the DTR with a focus on prioritizing alignment between the observed treatment trajectory and the one obtained by the optimal regime across decision stages. By relaxing the restriction that the observed trajectory must be fully aligned with the optimal treatments, our approach substantially improves the sample efficiency and stability of inverse probability weighted based methods. In particular, the proposed learning scheme builds a more general framework which includes the popular outcome weighted learning framework as a special case of ours. Moreover, we introduce the notion of stage importance scores along with an attention mechanism to explicitly account for heterogeneity among decision stages. We establish the theoretical properties of the proposed approach, including the Fisher consistency and finite-sample performance bound. Empirically, we evaluate the proposed method in extensive simulated environments and a real case study for COVID-19 pandemic.

Bi-Level Offline Policy Optimization with Limited Exploration

We study offline reinforcement learning (RL) which seeks to learn a good policy based on a fixed, pre-collected dataset. A fundamental challenge behind this task is the distributional shift due to the dataset lacking sufficient exploration, especially under function approximation. To tackle this issue, we propose a bi-level structured policy optimization algorithm that models a hierarchical interaction between the policy (upper-level) and the value function (lower-level). The lower level focuses on constructing a confidence set of value estimates that maintain sufficiently small weighted average Bellman errors, while controlling uncertainty arising from distribution mismatch. Subsequently, at the upper level, the policy aims to maximize a conservative value estimate from the confidence set formed at the lower level. This novel formulation preserves the maximum flexibility of the implicitly induced exploratory data distribution, enabling the power of model extrapolation. In practice, it can be solved through a computationally efficient, penalized adversarial estimation procedure. Our theoretical regret guarantees do not rely on any data-coverage and completeness-type assumptions, only requiring realizability. These guarantees also demonstrate that the learned policy represents the "best effort" among all policies, as no other policies can outperform it. We evaluate our model using a blend of synthetic, benchmark, and real-world datasets for offline RL, showing that it performs competitively with state-of-the-art methods.

Distributional Shift-Aware Off-Policy Interval Estimation: A Unified Error Quantification Framework

We study high-confidence off-policy evaluation in the context of infinite-horizon Markov decision processes, where the objective is to establish a confidence interval (CI) for the target policy value using only offline data pre-collected from unknown behavior policies. This task faces two primary challenges: providing a comprehensive and rigorous error quantification in CI estimation, and addressing the distributional shift that results from discrepancies between the distribution induced by the target policy and the offline data-generating process. Motivated by an innovative unified error analysis, we jointly quantify the two sources of estimation errors: the misspecification error on modeling marginalized importance weights and the statistical uncertainty due to sampling, within a single interval. This unified framework reveals a previously hidden tradeoff between the errors, which undermines the tightness of the CI. Relying on a carefully designed discriminator function, the proposed estimator achieves a dual purpose: breaking the curse of the tradeoff to attain the tightest possible CI, and adapting the CI to ensure robustness against distributional shifts. Our method is applicable to time-dependent data without assuming any weak dependence conditions via leveraging a local supermartingale/martingale structure. Theoretically, we show that our algorithm is sample-efficient, error-robust, and provably convergent even in non-linear function approximation settings. The numerical performance of the proposed method is examined in synthetic datasets and an OhioT1DM mobile health study.

A Model-Agnostic Graph Neural Network for Integrating Local and Global Information

Graph Neural Networks (GNNs) have achieved promising performance in a variety of graph-focused tasks. Despite their success, existing GNNs suffer from two significant limitations: a lack of interpretability in results due to their black-box nature, and an inability to learn representations of varying orders. To tackle these issues, we propose a novel Model-agnostic Graph Neural Network (MaGNet) framework, which is able to sequentially integrate information of various orders, extract knowledge from high-order neighbors, and provide meaningful and interpretable results by identifying influential compact graph structures. In particular, MaGNet consists of two components: an estimation model for the latent representation of complex relationships under graph topology, and an interpretation model that identifies influential nodes, edges, and important node features. Theoretically, we establish the generalization error bound for MaGNet via empirical Rademacher complexity, and showcase its power to represent layer-wise neighborhood mixing. We conduct comprehensive numerical studies using simulated data to demonstrate the superior performance of MaGNet in comparison to several state-of-the-art alternatives. Furthermore, we apply MaGNet to a real-world case study aimed at extracting task-critical information from brain activity data, thereby highlighting its effectiveness in advancing scientific research.

Stackelberg Batch Policy Learning

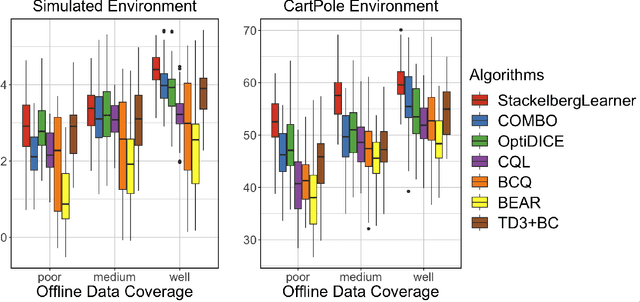
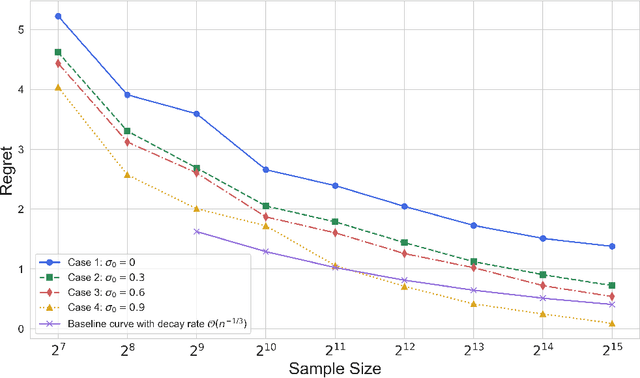
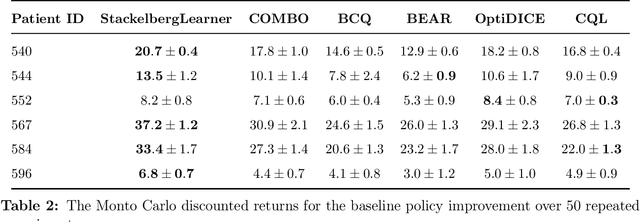
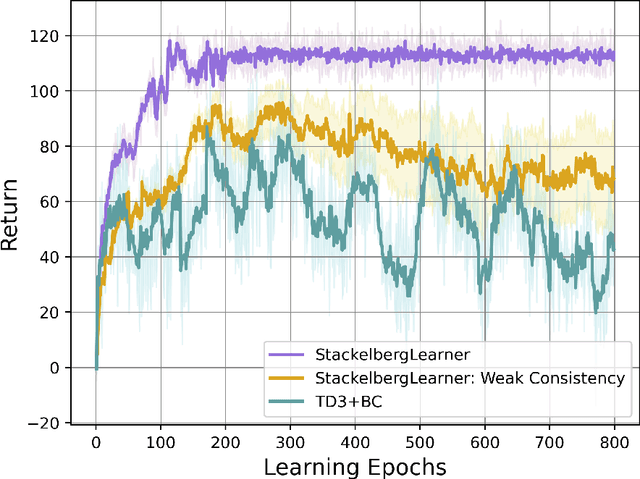
Batch reinforcement learning (RL) defines the task of learning from a fixed batch of data lacking exhaustive exploration. Worst-case optimality algorithms, which calibrate a value-function model class from logged experience and perform some type of pessimistic evaluation under the learned model, have emerged as a promising paradigm for batch RL. However, contemporary works on this stream have commonly overlooked the hierarchical decision-making structure hidden in the optimization landscape. In this paper, we adopt a game-theoretical viewpoint and model the policy learning diagram as a two-player general-sum game with a leader-follower structure. We propose a novel stochastic gradient-based learning algorithm: StackelbergLearner, in which the leader player updates according to the total derivative of its objective instead of the usual individual gradient, and the follower player makes individual updates and ensures transition-consistent pessimistic reasoning. The derived learning dynamic naturally lends StackelbergLearner to a game-theoretic interpretation and provides a convergence guarantee to differentiable Stackelberg equilibria. From a theoretical standpoint, we provide instance-dependent regret bounds with general function approximation, which shows that our algorithm can learn a best-effort policy that is able to compete against any comparator policy that is covered by batch data. Notably, our theoretical regret guarantees only require realizability without any data coverage and strong function approximation conditions, e.g., Bellman closedness, which is in contrast to prior works lacking such guarantees. Through comprehensive experiments, we find that our algorithm consistently performs as well or better as compared to state-of-the-art methods in batch RL benchmark and real-world datasets.

Quasi-optimal Learning with Continuous Treatments

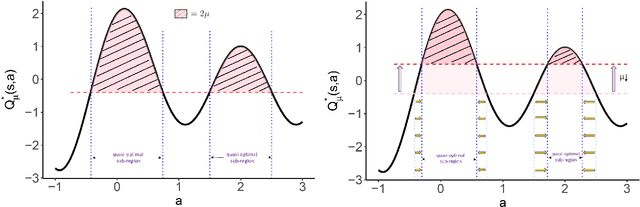
Many real-world applications of reinforcement learning (RL) require making decisions in continuous action environments. In particular, determining the optimal dose level plays a vital role in developing medical treatment regimes. One challenge in adapting existing RL algorithms to medical applications, however, is that the popular infinite support stochastic policies, e.g., Gaussian policy, may assign riskily high dosages and harm patients seriously. Hence, it is important to induce a policy class whose support only contains near-optimal actions, and shrink the action-searching area for effectiveness and reliability. To achieve this, we develop a novel \emph{quasi-optimal learning algorithm}, which can be easily optimized in off-policy settings with guaranteed convergence under general function approximations. Theoretically, we analyze the consistency, sample complexity, adaptability, and convergence of the proposed algorithm. We evaluate our algorithm with comprehensive simulated experiments and a dose suggestion real application to Ohio Type 1 diabetes dataset.

Estimating Optimal Infinite Horizon Dynamic Treatment Regimes via pT-Learning

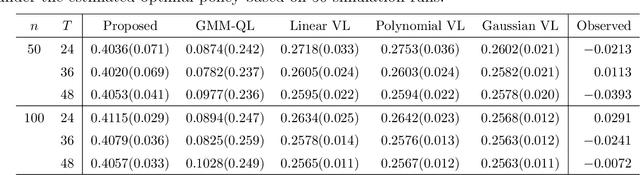
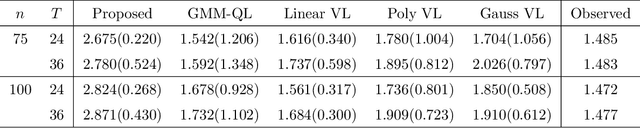
Recent advances in mobile health (mHealth) technology provide an effective way to monitor individuals' health statuses and deliver just-in-time personalized interventions. However, the practical use of mHealth technology raises unique challenges to existing methodologies on learning an optimal dynamic treatment regime. Many mHealth applications involve decision-making with large numbers of intervention options and under an infinite time horizon setting where the number of decision stages diverges to infinity. In addition, temporary medication shortages may cause optimal treatments to be unavailable, while it is unclear what alternatives can be used. To address these challenges, we propose a Proximal Temporal consistency Learning (pT-Learning) framework to estimate an optimal regime that is adaptively adjusted between deterministic and stochastic sparse policy models. The resulting minimax estimator avoids the double sampling issue in the existing algorithms. It can be further simplified and can easily incorporate off-policy data without mismatched distribution corrections. We study theoretical properties of the sparse policy and establish finite-sample bounds on the excess risk and performance error. The proposed method is implemented by our proximalDTR package and is evaluated through extensive simulation studies and the OhioT1DM mHealth dataset.

Multicategory Angle-based Learning for Estimating Optimal Dynamic Treatment Regimes with Censored Data

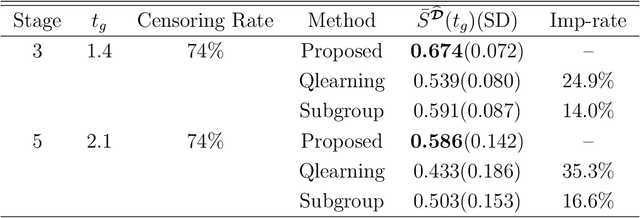
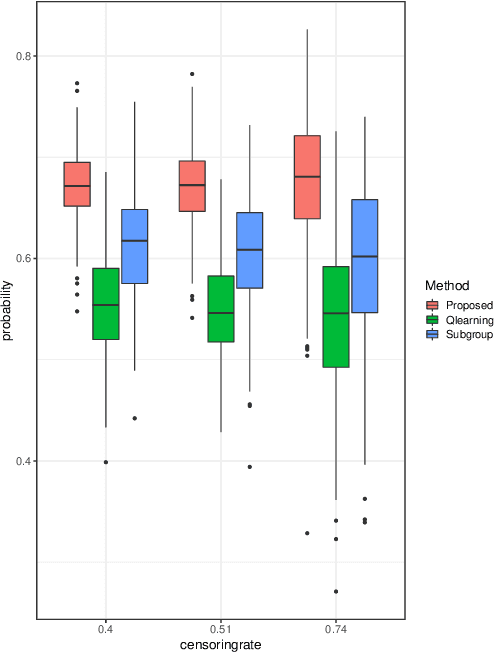
An optimal dynamic treatment regime (DTR) consists of a sequence of decision rules in maximizing long-term benefits, which is applicable for chronic diseases such as HIV infection or cancer. In this paper, we develop a novel angle-based approach to search the optimal DTR under a multicategory treatment framework for survival data. The proposed method targets maximization the conditional survival function of patients following a DTR. In contrast to most existing approaches which are designed to maximize the expected survival time under a binary treatment framework, the proposed method solves the multicategory treatment problem given multiple stages for censored data. Specifically, the proposed method obtains the optimal DTR via integrating estimations of decision rules at multiple stages into a single multicategory classification algorithm without imposing additional constraints, which is also more computationally efficient and robust. In theory, we establish Fisher consistency of the proposed method under regularity conditions. Our numerical studies show that the proposed method outperforms competing methods in terms of maximizing the conditional survival function. We apply the proposed method to two real datasets: Framingham heart study data and acquired immunodeficiency syndrome (AIDS) clinical data.