Ruoqing Zhu
Reinforcement Learning with Continuous Actions Under Unmeasured Confounding
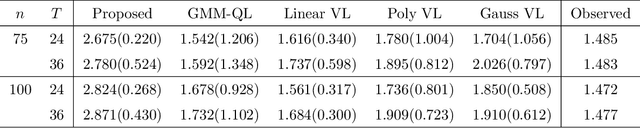
May 01, 2025Abstract:This paper addresses the challenge of offline policy learning in reinforcement learning with continuous action spaces when unmeasured confounders are present. While most existing research focuses on policy evaluation within partially observable Markov decision processes (POMDPs) and assumes discrete action spaces, we advance this field by establishing a novel identification result to enable the nonparametric estimation of policy value for a given target policy under an infinite-horizon framework. Leveraging this identification, we develop a minimax estimator and introduce a policy-gradient-based algorithm to identify the in-class optimal policy that maximizes the estimated policy value. Furthermore, we provide theoretical results regarding the consistency, finite-sample error bound, and regret bound of the resulting optimal policy. Extensive simulations and a real-world application using the German Family Panel data demonstrate the effectiveness of our proposed methodology.
AI in Pharma for Personalized Sequential Decision-Making: Methods, Applications and Opportunities
Nov 30, 2023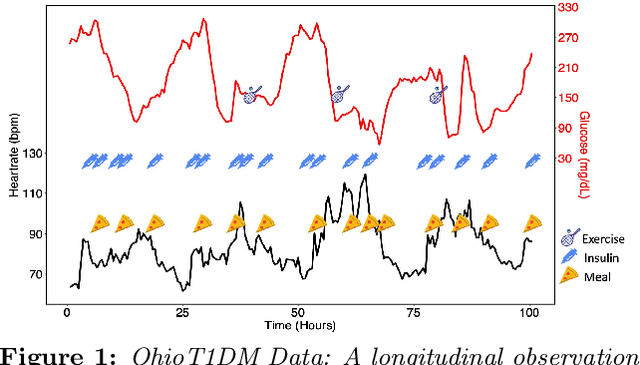
Abstract:In the pharmaceutical industry, the use of artificial intelligence (AI) has seen consistent growth over the past decade. This rise is attributed to major advancements in statistical machine learning methodologies, computational capabilities and the increased availability of large datasets. AI techniques are applied throughout different stages of drug development, ranging from drug discovery to post-marketing benefit-risk assessment. Kolluri et al. provided a review of several case studies that span these stages, featuring key applications such as protein structure prediction, success probability estimation, subgroup identification, and AI-assisted clinical trial monitoring. From a regulatory standpoint, there was a notable uptick in submissions incorporating AI components in 2021. The most prevalent therapeutic areas leveraging AI were oncology (27%), psychiatry (15%), gastroenterology (12%), and neurology (11%). The paradigm of personalized or precision medicine has gained significant traction in recent research, partly due to advancements in AI techniques \cite{hamburg2010path}. This shift has had a transformative impact on the pharmaceutical industry. Departing from the traditional "one-size-fits-all" model, personalized medicine incorporates various individual factors, such as environmental conditions, lifestyle choices, and health histories, to formulate customized treatment plans. By utilizing sophisticated machine learning algorithms, clinicians and researchers are better equipped to make informed decisions in areas such as disease prevention, diagnosis, and treatment selection, thereby optimizing health outcomes for each individual.
Stage-Aware Learning for Dynamic Treatments
Oct 30, 2023



Abstract:Recent advances in dynamic treatment regimes (DTRs) provide powerful optimal treatment searching algorithms, which are tailored to individuals' specific needs and able to maximize their expected clinical benefits. However, existing algorithms could suffer from insufficient sample size under optimal treatments, especially for chronic diseases involving long stages of decision-making. To address these challenges, we propose a novel individualized learning method which estimates the DTR with a focus on prioritizing alignment between the observed treatment trajectory and the one obtained by the optimal regime across decision stages. By relaxing the restriction that the observed trajectory must be fully aligned with the optimal treatments, our approach substantially improves the sample efficiency and stability of inverse probability weighted based methods. In particular, the proposed learning scheme builds a more general framework which includes the popular outcome weighted learning framework as a special case of ours. Moreover, we introduce the notion of stage importance scores along with an attention mechanism to explicitly account for heterogeneity among decision stages. We establish the theoretical properties of the proposed approach, including the Fisher consistency and finite-sample performance bound. Empirically, we evaluate the proposed method in extensive simulated environments and a real case study for COVID-19 pandemic.
Distributional Shift-Aware Off-Policy Interval Estimation: A Unified Error Quantification Framework
Oct 02, 2023Abstract:We study high-confidence off-policy evaluation in the context of infinite-horizon Markov decision processes, where the objective is to establish a confidence interval (CI) for the target policy value using only offline data pre-collected from unknown behavior policies. This task faces two primary challenges: providing a comprehensive and rigorous error quantification in CI estimation, and addressing the distributional shift that results from discrepancies between the distribution induced by the target policy and the offline data-generating process. Motivated by an innovative unified error analysis, we jointly quantify the two sources of estimation errors: the misspecification error on modeling marginalized importance weights and the statistical uncertainty due to sampling, within a single interval. This unified framework reveals a previously hidden tradeoff between the errors, which undermines the tightness of the CI. Relying on a carefully designed discriminator function, the proposed estimator achieves a dual purpose: breaking the curse of the tradeoff to attain the tightest possible CI, and adapting the CI to ensure robustness against distributional shifts. Our method is applicable to time-dependent data without assuming any weak dependence conditions via leveraging a local supermartingale/martingale structure. Theoretically, we show that our algorithm is sample-efficient, error-robust, and provably convergent even in non-linear function approximation settings. The numerical performance of the proposed method is examined in synthetic datasets and an OhioT1DM mobile health study.
Quasi-optimal Learning with Continuous Treatments
Jan 21, 2023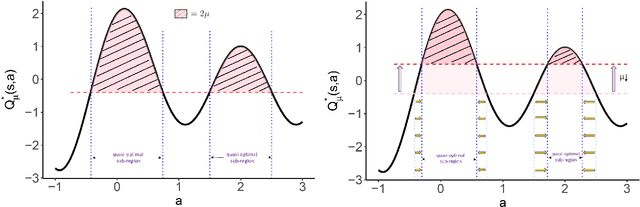



Abstract:Many real-world applications of reinforcement learning (RL) require making decisions in continuous action environments. In particular, determining the optimal dose level plays a vital role in developing medical treatment regimes. One challenge in adapting existing RL algorithms to medical applications, however, is that the popular infinite support stochastic policies, e.g., Gaussian policy, may assign riskily high dosages and harm patients seriously. Hence, it is important to induce a policy class whose support only contains near-optimal actions, and shrink the action-searching area for effectiveness and reliability. To achieve this, we develop a novel \emph{quasi-optimal learning algorithm}, which can be easily optimized in off-policy settings with guaranteed convergence under general function approximations. Theoretically, we analyze the consistency, sample complexity, adaptability, and convergence of the proposed algorithm. We evaluate our algorithm with comprehensive simulated experiments and a dose suggestion real application to Ohio Type 1 diabetes dataset.
Calibrate and Debias Layer-wise Sampling for Graph Convolutional Networks
Jun 01, 2022
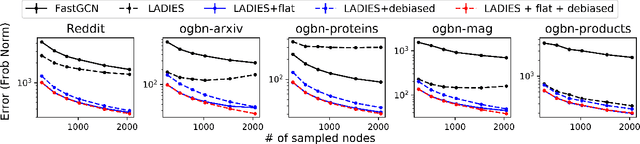
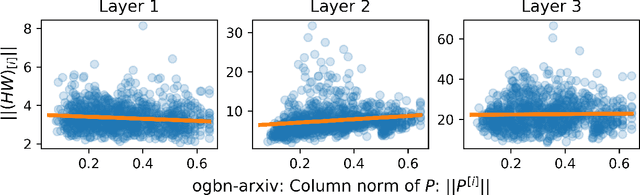

Abstract:To accelerate the training of graph convolutional networks (GCNs), many sampling-based methods have been developed for approximating the embedding aggregation. Among them, a layer-wise approach recursively performs importance sampling to select neighbors jointly for existing nodes in each layer. This paper revisits the approach from a matrix approximation perspective. We identify two issues in the existing layer-wise sampling methods: sub-optimal sampling probabilities and the approximation bias induced by sampling without replacement. We propose two remedies: new sampling probabilities and a debiasing algorithm, to address these issues, and provide the statistical analysis of the estimation variance. The improvements are demonstrated by extensive analyses and experiments on common benchmarks.
Confidence Band Estimation for Survival Random Forests
Apr 26, 2022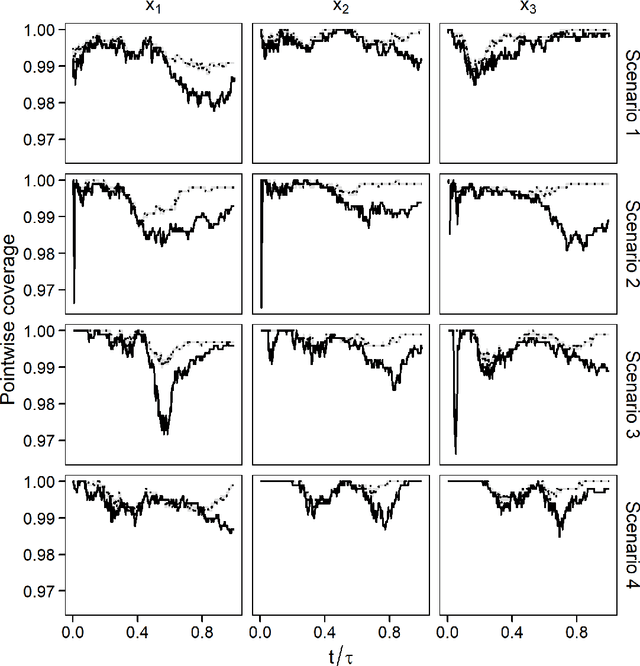
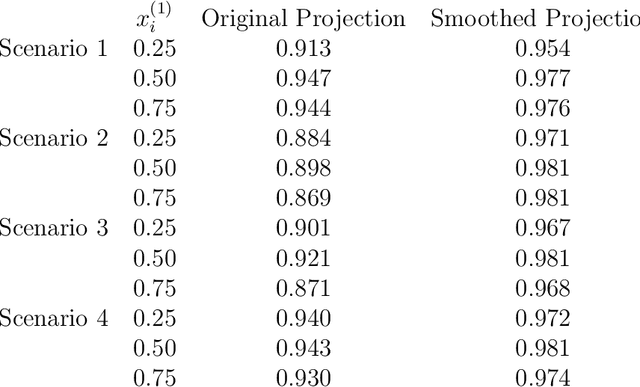
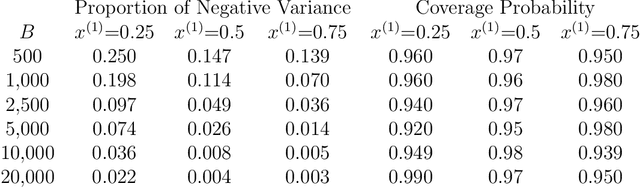
Abstract:Survival random forest is a popular machine learning tool for modeling censored survival data. However, there is currently no statistically valid and computationally feasible approach for estimating its confidence band. This paper proposes an unbiased confidence band estimation by extending recent developments in infinite-order incomplete U-statistics. The idea is to estimate the variance-covariance matrix of the cumulative hazard function prediction on a grid of time points. We then generate the confidence band by viewing the cumulative hazard function estimation as a Gaussian process whose distribution can be approximated through simulation. This approach is computationally easy to implement when the subsampling size of a tree is no larger than half of the total training sample size. Numerical studies show that our proposed method accurately estimates the confidence band and achieves desired coverage rate. We apply this method to veterans' administration lung cancer data.
On Variance Estimation of Random Forests
Feb 18, 2022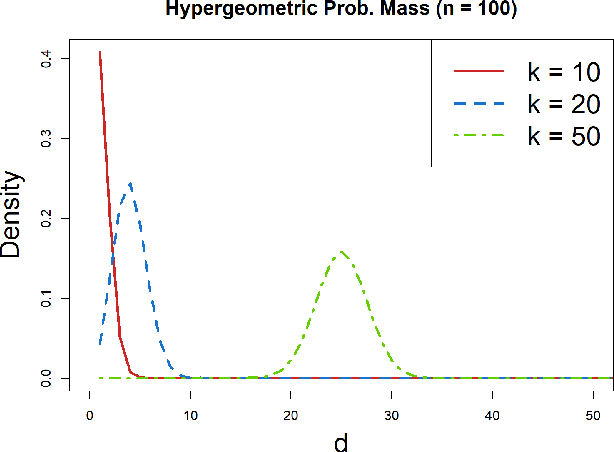
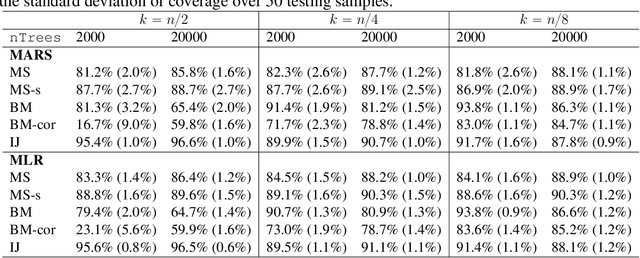
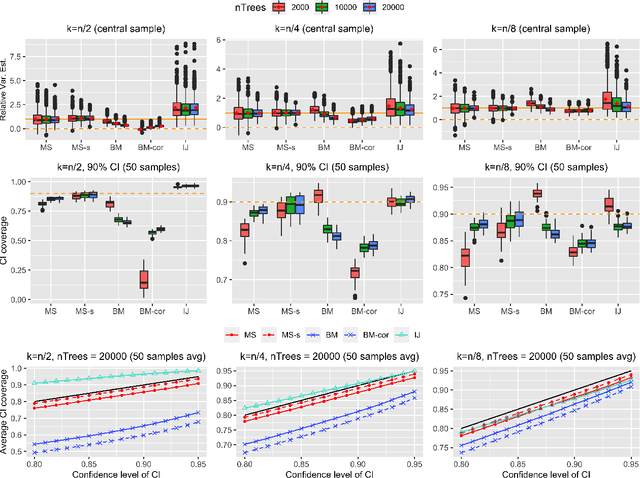
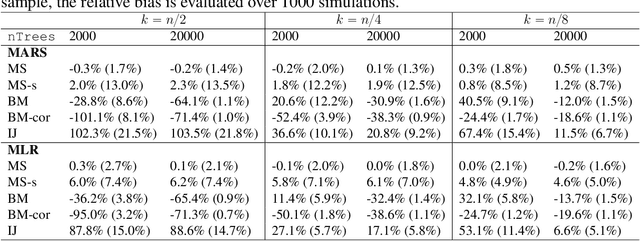
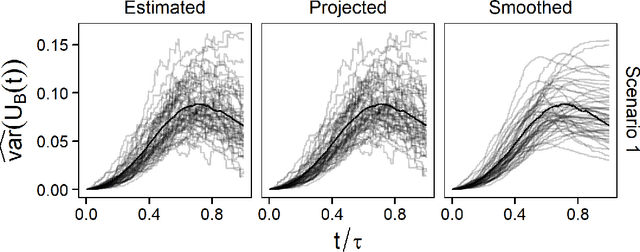
Abstract:Ensemble methods based on subsampling, such as random forests, are popular in applications due to their high predictive accuracy. Existing literature views a random forest prediction as an infinite-order incomplete U-statistic to quantify its uncertainty. However, these methods focus on a small subsampling size of each tree, which is theoretically valid but practically limited. This paper develops an unbiased variance estimator based on incomplete U-statistics, which allows the tree size to be comparable with the overall sample size, making statistical inference possible in a broader range of real applications. Simulation results demonstrate that our estimators enjoy lower bias and more accurate confidence interval coverage without additional computational costs. We also propose a local smoothing procedure to reduce the variation of our estimator, which shows improved numerical performance when the number of trees is relatively small. Further, we investigate the ratio consistency of our proposed variance estimator under specific scenarios. In particular, we develop a new "double U-statistic" formulation to analyze the Hoeffding decomposition of the estimator's variance.
Random Forests Weighted Local Fréchet Regression with Theoretical Guarantee
Feb 10, 2022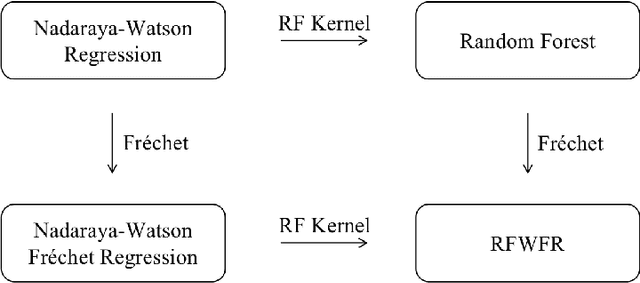
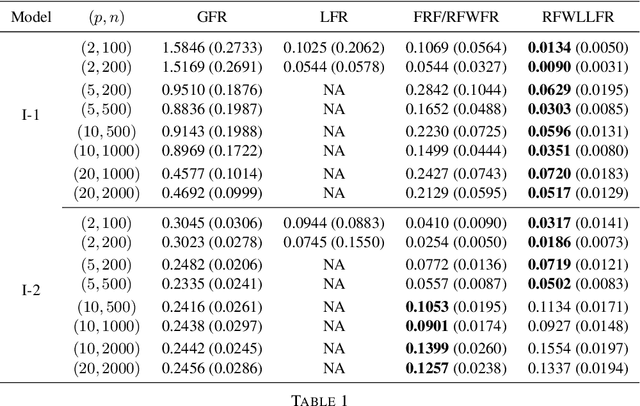
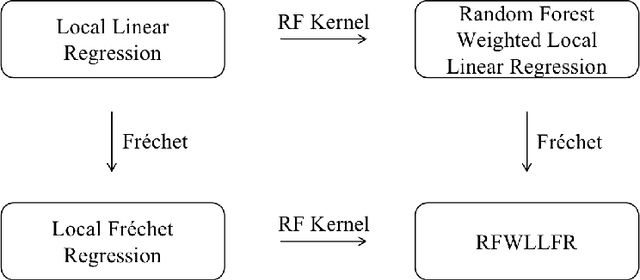

Abstract:Statistical analysis is increasingly confronted with complex data from general metric spaces, such as symmetric positive definite matrix-valued data and probability distribution functions. [47] and [17] establish a general paradigm of Fr\'echet regression with complex metric space valued responses and Euclidean predictors. However, their proposed local Fr\'echet regression approach involves nonparametric kernel smoothing and suffers from the curse of dimensionality. To address this issue, we in this paper propose a novel random forests weighted local Fr\'echet regression paradigm. The main mechanism of our approach relies on the adaptive kernels generated by random forests. Our first method utilizes these weights as the local average to solve the Fr\'echet mean, while the second method performs local linear Fr\'echet regression, making both methods locally adaptive. Our proposals significantly improve existing Fr\'echet regression methods. Based on the theory of infinite order U-processes and infinite order Mmn-estimator, we establish the consistency, rate of convergence, and asymptotic normality for our proposed random forests weighted Fr\'echet regression estimator, which covers the current large sample theory of random forests with Euclidean responses as a special case. Numerical studies show the superiority of our proposed two methods for Fr\'echet regression with several commonly encountered types of responses such as probability distribution functions, symmetric positive definite matrices, and sphere data. The practical merits of our proposals are also demonstrated through the application to the human mortality distribution data.
Estimating Optimal Infinite Horizon Dynamic Treatment Regimes via pT-Learning
Oct 20, 2021
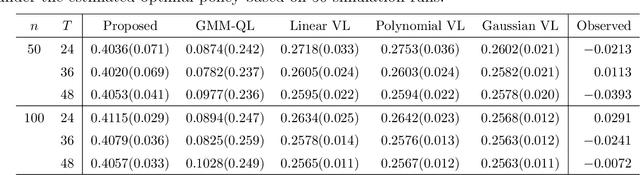

Abstract:Recent advances in mobile health (mHealth) technology provide an effective way to monitor individuals' health statuses and deliver just-in-time personalized interventions. However, the practical use of mHealth technology raises unique challenges to existing methodologies on learning an optimal dynamic treatment regime. Many mHealth applications involve decision-making with large numbers of intervention options and under an infinite time horizon setting where the number of decision stages diverges to infinity. In addition, temporary medication shortages may cause optimal treatments to be unavailable, while it is unclear what alternatives can be used. To address these challenges, we propose a Proximal Temporal consistency Learning (pT-Learning) framework to estimate an optimal regime that is adaptively adjusted between deterministic and stochastic sparse policy models. The resulting minimax estimator avoids the double sampling issue in the existing algorithms. It can be further simplified and can easily incorporate off-policy data without mismatched distribution corrections. We study theoretical properties of the sparse policy and establish finite-sample bounds on the excess risk and performance error. The proposed method is implemented by our proximalDTR package and is evaluated through extensive simulation studies and the OhioT1DM mHealth dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge