Testing Conditional Mean Independence Using Generative Neural Networks

Conditional mean independence (CMI) testing is crucial for statistical tasks including model determination and variable importance evaluation. In this work, we introduce a novel population CMI measure and a bootstrap-based testing procedure that utilizes deep generative neural networks to estimate the conditional mean functions involved in the population measure. The test statistic is thoughtfully constructed to ensure that even slowly decaying nonparametric estimation errors do not affect the asymptotic accuracy of the test. Our approach demonstrates strong empirical performance in scenarios with high-dimensional covariates and response variable, can handle multivariate responses, and maintains nontrivial power against local alternatives outside an $n^{-1/2}$ neighborhood of the null hypothesis. We also use numerical simulations and real-world imaging data applications to highlight the efficacy and versatility of our testing procedure.

Doubly Robust Conditional Independence Testing with Generative Neural Networks

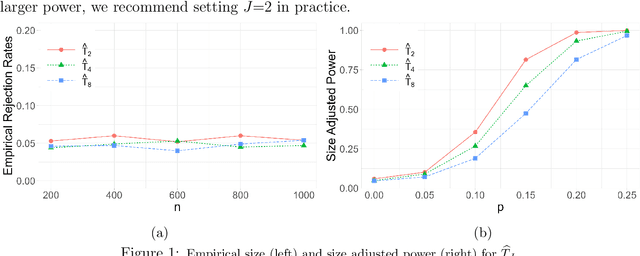
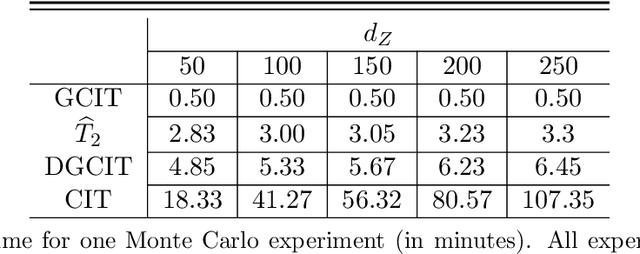
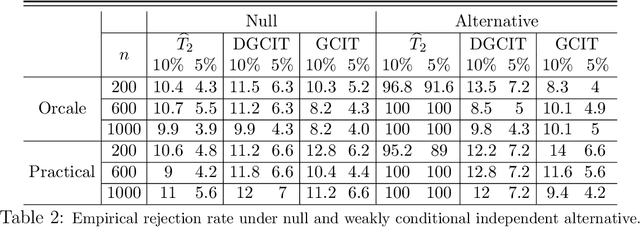
This article addresses the problem of testing the conditional independence of two generic random vectors $X$ and $Y$ given a third random vector $Z$, which plays an important role in statistical and machine learning applications. We propose a new non-parametric testing procedure that avoids explicitly estimating any conditional distributions but instead requires sampling from the two marginal conditional distributions of $X$ given $Z$ and $Y$ given $Z$. We further propose using a generative neural network (GNN) framework to sample from these approximated marginal conditional distributions, which tends to mitigate the curse of dimensionality due to its adaptivity to any low-dimensional structures and smoothness underlying the data. Theoretically, our test statistic is shown to enjoy a doubly robust property against GNN approximation errors, meaning that the test statistic retains all desirable properties of the oracle test statistic utilizing the true marginal conditional distributions, as long as the product of the two approximation errors decays to zero faster than the parametric rate. Asymptotic properties of our statistic and the consistency of a bootstrap procedure are derived under both null and local alternatives. Extensive numerical experiments and real data analysis illustrate the effectiveness and broad applicability of our proposed test.

On Variance Estimation of Random Forests

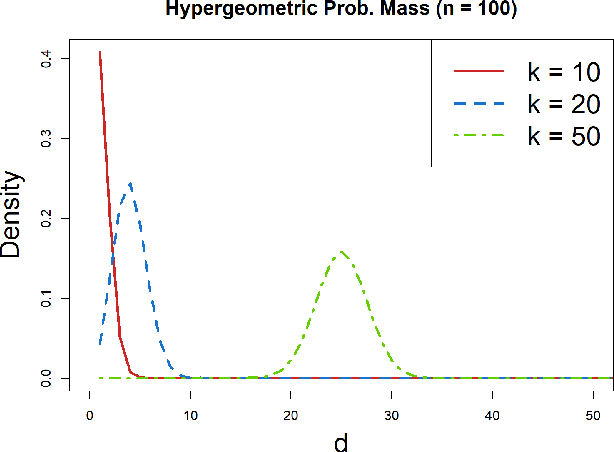
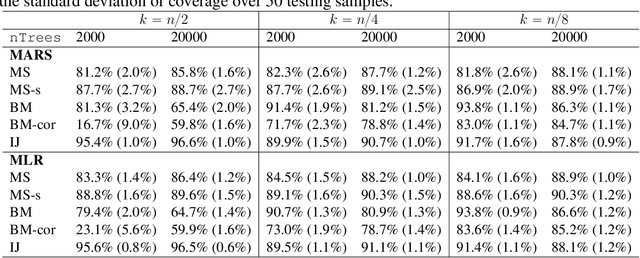
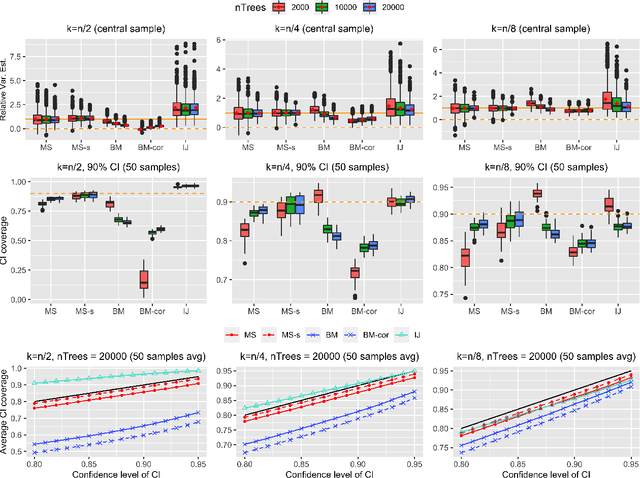
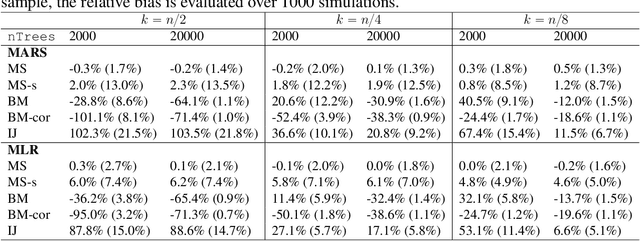
Ensemble methods based on subsampling, such as random forests, are popular in applications due to their high predictive accuracy. Existing literature views a random forest prediction as an infinite-order incomplete U-statistic to quantify its uncertainty. However, these methods focus on a small subsampling size of each tree, which is theoretically valid but practically limited. This paper develops an unbiased variance estimator based on incomplete U-statistics, which allows the tree size to be comparable with the overall sample size, making statistical inference possible in a broader range of real applications. Simulation results demonstrate that our estimators enjoy lower bias and more accurate confidence interval coverage without additional computational costs. We also propose a local smoothing procedure to reduce the variation of our estimator, which shows improved numerical performance when the number of trees is relatively small. Further, we investigate the ratio consistency of our proposed variance estimator under specific scenarios. In particular, we develop a new "double U-statistic" formulation to analyze the Hoeffding decomposition of the estimator's variance.