SERM: Self-Evolving Relevance Model with Agent-Driven Learning from Massive Query Streams

Due to the dynamically evolving nature of real-world query streams, relevance models struggle to generalize to practical search scenarios. A sophisticated solution is self-evolution techniques. However, in large-scale industrial settings with massive query streams, this technique faces two challenges: (1) informative samples are often sparse and difficult to identify, and (2) pseudo-labels generated by the current model could be unreliable. To address these challenges, in this work, we propose a Self-Evolving Relevance Model approach (SERM), which comprises two complementary multi-agent modules: a multi-agent sample miner, designed to detect distributional shifts and identify informative training samples, and a multi-agent relevance annotator, which provides reliable labels through a two-level agreement framework. We evaluate SERM in a large-scale industrial setting, which serves billions of user requests daily. Experimental results demonstrate that SERM can achieve significant performance gains through iterative self-evolution, as validated by extensive offline multilingual evaluations and online testing.

Simulation-based Inference via Langevin Dynamics with Score Matching

Simulation-based inference (SBI) enables Bayesian analysis when the likelihood is intractable but model simulations are available. Recent advances in statistics and machine learning, including Approximate Bayesian Computation and deep generative models, have expanded the applicability of SBI, yet these methods often face challenges in moderate to high-dimensional parameter spaces. Motivated by the success of gradient-based Monte Carlo methods in Bayesian sampling, we propose a novel SBI method that integrates score matching with Langevin dynamics to explore complex posterior landscapes more efficiently in such settings. Our approach introduces tailored score-matching procedures for SBI, including a localization scheme that reduces simulation costs and an architectural regularization that embeds the statistical structure of log-likelihood scores to improve score-matching accuracy. We provide theoretical analysis of the method and illustrate its practical benefits on benchmark tasks and on more challenging problems in moderate to high dimensions, where it performs favorably compared to existing approaches.

Hunyuan-TurboS: Advancing Large Language Models through Mamba-Transformer Synergy and Adaptive Chain-of-Thought

As Large Language Models (LLMs) rapidly advance, we introduce Hunyuan-TurboS, a novel large hybrid Transformer-Mamba Mixture of Experts (MoE) model. It synergistically combines Mamba's long-sequence processing efficiency with Transformer's superior contextual understanding. Hunyuan-TurboS features an adaptive long-short chain-of-thought (CoT) mechanism, dynamically switching between rapid responses for simple queries and deep "thinking" modes for complex problems, optimizing computational resources. Architecturally, this 56B activated (560B total) parameter model employs 128 layers (Mamba2, Attention, FFN) with an innovative AMF/MF block pattern. Faster Mamba2 ensures linear complexity, Grouped-Query Attention minimizes KV cache, and FFNs use an MoE structure. Pre-trained on 16T high-quality tokens, it supports a 256K context length and is the first industry-deployed large-scale Mamba model. Our comprehensive post-training strategy enhances capabilities via Supervised Fine-Tuning (3M instructions), a novel Adaptive Long-short CoT Fusion method, Multi-round Deliberation Learning for iterative improvement, and a two-stage Large-scale Reinforcement Learning process targeting STEM and general instruction-following. Evaluations show strong performance: overall top 7 rank on LMSYS Chatbot Arena with a score of 1356, outperforming leading models like Gemini-2.0-Flash-001 (1352) and o4-mini-2025-04-16 (1345). TurboS also achieves an average of 77.9% across 23 automated benchmarks. Hunyuan-TurboS balances high performance and efficiency, offering substantial capabilities at lower inference costs than many reasoning models, establishing a new paradigm for efficient large-scale pre-trained models.

Embedding Empirical Distributions for Computing Optimal Transport Maps

Distributional data have become increasingly prominent in modern signal processing, highlighting the necessity of computing optimal transport (OT) maps across multiple probability distributions. Nevertheless, recent studies on neural OT methods predominantly focused on the efficient computation of a single map between two distributions. To address this challenge, we introduce a novel approach to learning transport maps for new empirical distributions. Specifically, we employ the transformer architecture to produce embeddings from distributional data of varying length; these embeddings are then fed into a hypernetwork to generate neural OT maps. Various numerical experiments were conducted to validate the embeddings and the generated OT maps. The model implementation and the code are provided on https://github.com/jiangmingchen/HOTET.

Unveiling Contrastive Learning's Capability of Neighborhood Aggregation for Collaborative Filtering

Personalized recommendation is widely used in the web applications, and graph contrastive learning (GCL) has gradually become a dominant approach in recommender systems, primarily due to its ability to extract self-supervised signals from raw interaction data, effectively alleviating the problem of data sparsity. A classic GCL-based method typically uses data augmentation during graph convolution to generates more contrastive views, and performs contrast on these new views to obtain rich self-supervised signals. Despite this paradigm is effective, the reasons behind the performance gains remain a mystery. In this paper, we first reveal via theoretical derivation that the gradient descent process of the CL objective is formally equivalent to graph convolution, which implies that CL objective inherently supports neighborhood aggregation on interaction graphs. We further substantiate this capability through experimental validation and identify common misconceptions in the selection of positive samples in previous methods, which limit the potential of CL objective. Based on this discovery, we propose the Light Contrastive Collaborative Filtering (LightCCF) method, which introduces a novel neighborhood aggregation objective to bring users closer to all interacted items while pushing them away from other positive pairs, thus achieving high-quality neighborhood aggregation with very low time complexity. On three highly sparse public datasets, the proposed method effectively aggregate neighborhood information while preventing graph over-smoothing, demonstrating significant improvements over existing GCL-based counterparts in both training efficiency and recommendation accuracy. Our implementations are publicly accessible.

NuWa: Deriving Lightweight Task-Specific Vision Transformers for Edge Devices

Vision Transformers (ViTs) excel in computer vision tasks but lack flexibility for edge devices' diverse needs. A vital issue is that ViTs pre-trained to cover a broad range of tasks are \textit{over-qualified} for edge devices that usually demand only part of a ViT's knowledge for specific tasks. Their task-specific accuracy on these edge devices is suboptimal. We discovered that small ViTs that focus on device-specific tasks can improve model accuracy and in the meantime, accelerate model inference. This paper presents NuWa, an approach that derives small ViTs from the base ViT for edge devices with specific task requirements. NuWa can transfer task-specific knowledge extracted from the base ViT into small ViTs that fully leverage constrained resources on edge devices to maximize model accuracy with inference latency assurance. Experiments with three base ViTs on three public datasets demonstrate that compared with state-of-the-art solutions, NuWa improves model accuracy by up to $\text{11.83}\%$ and accelerates model inference by 1.29$\times$ - 2.79$\times$. Code for reproduction is available at https://anonymous.4open.science/r/Task_Specific-3A5E.

Testing Conditional Mean Independence Using Generative Neural Networks

Conditional mean independence (CMI) testing is crucial for statistical tasks including model determination and variable importance evaluation. In this work, we introduce a novel population CMI measure and a bootstrap-based testing procedure that utilizes deep generative neural networks to estimate the conditional mean functions involved in the population measure. The test statistic is thoughtfully constructed to ensure that even slowly decaying nonparametric estimation errors do not affect the asymptotic accuracy of the test. Our approach demonstrates strong empirical performance in scenarios with high-dimensional covariates and response variable, can handle multivariate responses, and maintains nontrivial power against local alternatives outside an $n^{-1/2}$ neighborhood of the null hypothesis. We also use numerical simulations and real-world imaging data applications to highlight the efficacy and versatility of our testing procedure.

A Likelihood Based Approach to Distribution Regression Using Conditional Deep Generative Models

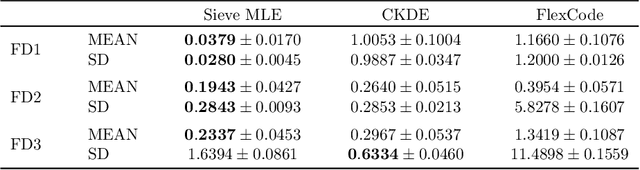
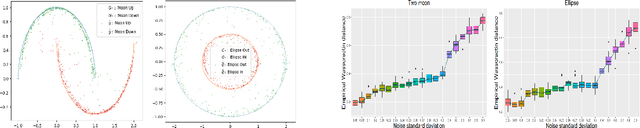
In this work, we explore the theoretical properties of conditional deep generative models under the statistical framework of distribution regression where the response variable lies in a high-dimensional ambient space but concentrates around a potentially lower-dimensional manifold. More specifically, we study the large-sample properties of a likelihood-based approach for estimating these models. Our results lead to the convergence rate of a sieve maximum likelihood estimator (MLE) for estimating the conditional distribution (and its devolved counterpart) of the response given predictors in the Hellinger (Wasserstein) metric. Our rates depend solely on the intrinsic dimension and smoothness of the true conditional distribution. These findings provide an explanation of why conditional deep generative models can circumvent the curse of dimensionality from the perspective of statistical foundations and demonstrate that they can learn a broader class of nearly singular conditional distributions. Our analysis also emphasizes the importance of introducing a small noise perturbation to the data when they are supported sufficiently close to a manifold. Finally, in our numerical studies, we demonstrate the effective implementation of the proposed approach using both synthetic and real-world datasets, which also provide complementary validation to our theoretical findings.

Doubly Robust Conditional Independence Testing with Generative Neural Networks

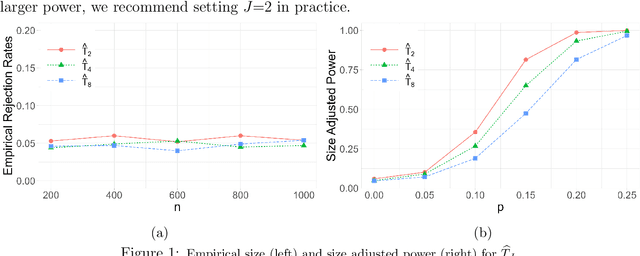
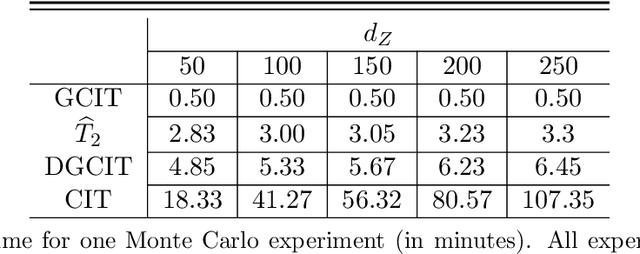
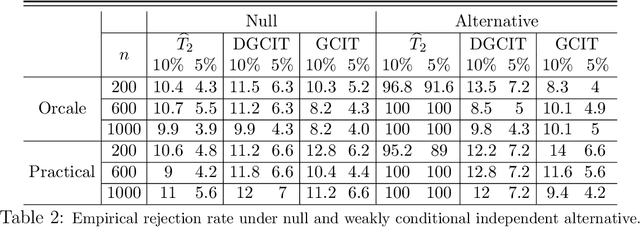
This article addresses the problem of testing the conditional independence of two generic random vectors $X$ and $Y$ given a third random vector $Z$, which plays an important role in statistical and machine learning applications. We propose a new non-parametric testing procedure that avoids explicitly estimating any conditional distributions but instead requires sampling from the two marginal conditional distributions of $X$ given $Z$ and $Y$ given $Z$. We further propose using a generative neural network (GNN) framework to sample from these approximated marginal conditional distributions, which tends to mitigate the curse of dimensionality due to its adaptivity to any low-dimensional structures and smoothness underlying the data. Theoretically, our test statistic is shown to enjoy a doubly robust property against GNN approximation errors, meaning that the test statistic retains all desirable properties of the oracle test statistic utilizing the true marginal conditional distributions, as long as the product of the two approximation errors decays to zero faster than the parametric rate. Asymptotic properties of our statistic and the consistency of a bootstrap procedure are derived under both null and local alternatives. Extensive numerical experiments and real data analysis illustrate the effectiveness and broad applicability of our proposed test.

CHASE: A Causal Heterogeneous Graph based Framework for Root Cause Analysis in Multimodal Microservice Systems

In recent years, the widespread adoption of distributed microservice architectures within the industry has significantly increased the demand for enhanced system availability and robustness. Due to the complex service invocation paths and dependencies at enterprise-level microservice systems, it is challenging to locate the anomalies promptly during service invocations, thus causing intractable issues for normal system operations and maintenance. In this paper, we propose a Causal Heterogeneous grAph baSed framEwork for root cause analysis, namely CHASE, for microservice systems with multimodal data, including traces, logs, and system monitoring metrics. Specifically, related information is encoded into representative embeddings and further modeled by a multimodal invocation graph. Following that, anomaly detection is performed on each instance node with attentive heterogeneous message passing from its adjacent metric and log nodes. Finally, CHASE learns from the constructed hypergraph with hyperedges representing the flow of causality and performs root cause localization. We evaluate the proposed framework on two public microservice datasets with distinct attributes and compare with the state-of-the-art methods. The results show that CHASE achieves the average performance gain up to 36.2%(A@1) and 29.4%(Percentage@1), respectively to its best counterpart.