A Likelihood Based Approach to Distribution Regression Using Conditional Deep Generative Models

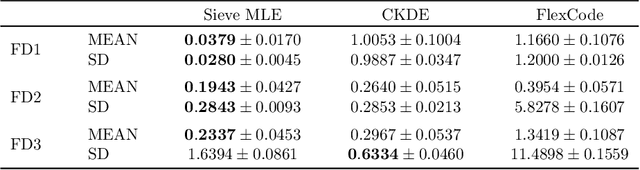
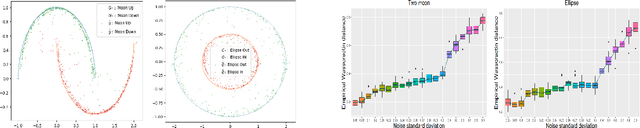
In this work, we explore the theoretical properties of conditional deep generative models under the statistical framework of distribution regression where the response variable lies in a high-dimensional ambient space but concentrates around a potentially lower-dimensional manifold. More specifically, we study the large-sample properties of a likelihood-based approach for estimating these models. Our results lead to the convergence rate of a sieve maximum likelihood estimator (MLE) for estimating the conditional distribution (and its devolved counterpart) of the response given predictors in the Hellinger (Wasserstein) metric. Our rates depend solely on the intrinsic dimension and smoothness of the true conditional distribution. These findings provide an explanation of why conditional deep generative models can circumvent the curse of dimensionality from the perspective of statistical foundations and demonstrate that they can learn a broader class of nearly singular conditional distributions. Our analysis also emphasizes the importance of introducing a small noise perturbation to the data when they are supported sufficiently close to a manifold. Finally, in our numerical studies, we demonstrate the effective implementation of the proposed approach using both synthetic and real-world datasets, which also provide complementary validation to our theoretical findings.

HistoSPACE: Histology-Inspired Spatial Transcriptome Prediction And Characterization Engine

Spatial transcriptomics (ST) enables the visualization of gene expression within the context of tissue morphology. This emerging discipline has the potential to serve as a foundation for developing tools to design precision medicines. However, due to the higher costs and expertise required for such experiments, its translation into a regular clinical practice might be challenging. Despite the implementation of modern deep learning to enhance information obtained from histological images using AI, efforts have been constrained by limitations in the diversity of information. In this paper, we developed a model, HistoSPACE that explore the diversity of histological images available with ST data to extract molecular insights from tissue image. Our proposed study built an image encoder derived from universal image autoencoder. This image encoder was connected to convolution blocks to built the final model. It was further fine tuned with the help of ST-Data. This model is notably lightweight in compared to traditional histological models. Our developed model demonstrates significant efficiency compared to contemporary algorithms, revealing a correlation of 0.56 in leave-one-out cross-validation. Finally, its robustness was validated through an independent dataset, showing a well matched preditction with predefined disease pathology.

Unmasking unlearnable models: a classification challenge for biomedical images without visible cues

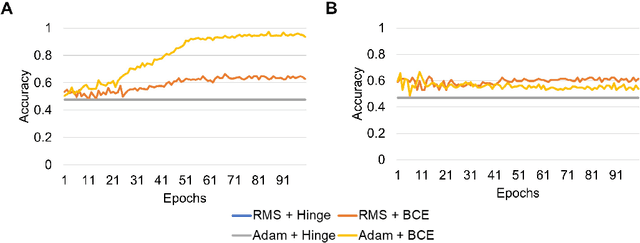
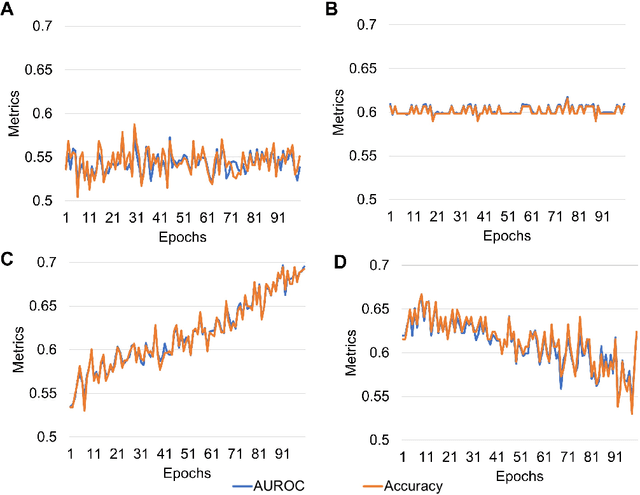
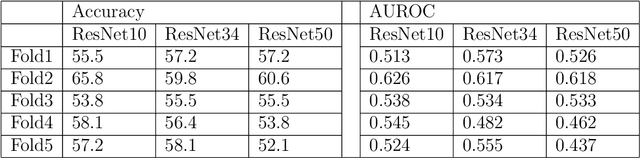
Predicting traits from images lacking visual cues is challenging, as algorithms are designed to capture visually correlated ground truth. This problem is critical in biomedical sciences, and their solution can improve the efficacy of non-invasive methods. For example, a recent challenge of predicting MGMT methylation status from MRI images is critical for treatment decisions of glioma patients. Using less robust models poses a significant risk in these critical scenarios and underscores the urgency of addressing this issue. Despite numerous efforts, contemporary models exhibit suboptimal performance, and underlying reasons for this limitation remain elusive. In this study, we demystify the complexity of MGMT status prediction through a comprehensive exploration by performing benchmarks of existing models adjoining transfer learning. Their architectures were further dissected by observing gradient flow across layers. Additionally, a feature selection strategy was applied to improve model interpretability. Our finding highlighted that current models are unlearnable and may require new architectures to explore applications in the real world. We believe our study will draw immediate attention and catalyse advancements in predictive modelling with non-visible cues.

A Globally Convergent Gradient-based Bilevel Hyperparameter Optimization Method

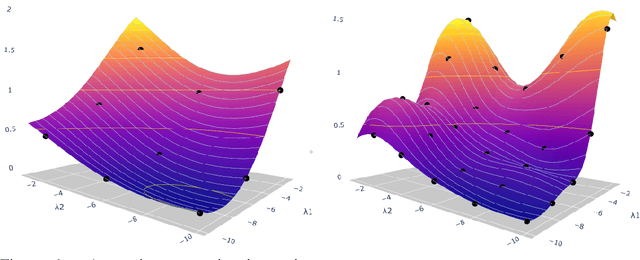
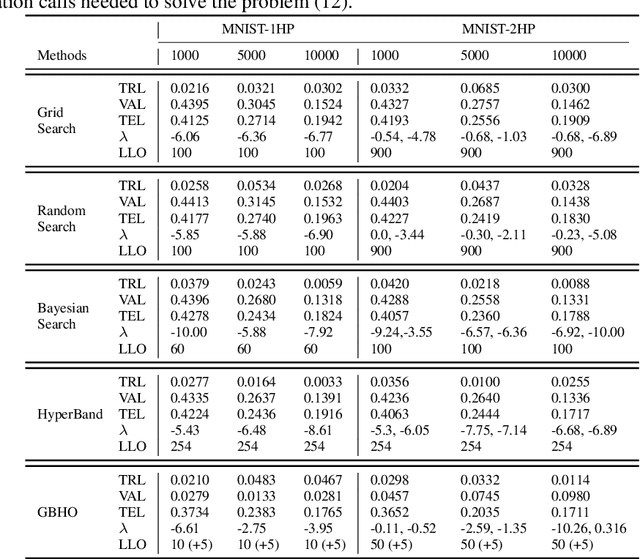
Hyperparameter optimization in machine learning is often achieved using naive techniques that only lead to an approximate set of hyperparameters. Although techniques such as Bayesian optimization perform an intelligent search on a given domain of hyperparameters, it does not guarantee an optimal solution. A major drawback of most of these approaches is an exponential increase of their search domain with number of hyperparameters, increasing the computational cost and making the approaches slow. The hyperparameter optimization problem is inherently a bilevel optimization task, and some studies have attempted bilevel solution methodologies for solving this problem. However, these studies assume a unique set of model weights that minimize the training loss, which is generally violated by deep learning architectures. This paper discusses a gradient-based bilevel method addressing these drawbacks for solving the hyperparameter optimization problem. The proposed method can handle continuous hyperparameters for which we have chosen the regularization hyperparameter in our experiments. The method guarantees convergence to the set of optimal hyperparameters that this study has theoretically proven. The idea is based on approximating the lower-level optimal value function using Gaussian process regression. As a result, the bilevel problem is reduced to a single level constrained optimization task that is solved using the augmented Lagrangian method. We have performed an extensive computational study on the MNIST and CIFAR-10 datasets on multi-layer perceptron and LeNet architectures that confirms the efficiency of the proposed method. A comparative study against grid search, random search, Bayesian optimization, and HyberBand method on various hyperparameter problems shows that the proposed algorithm converges with lower computation and leads to models that generalize better on the testing set.