Decomposition of Difficulties in Complex Optimization Problems Using a Bilevel Approach

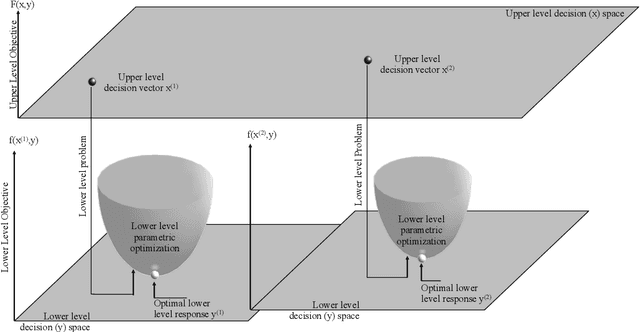
Practical optimization problems may contain different kinds of difficulties that are often not tractable if one relies on a particular optimization method. Different optimization approaches offer different strengths that are good at tackling one or more difficulty in an optimization problem. For instance, evolutionary algorithms have a niche in handling complexities like discontinuity, non-differentiability, discreteness and non-convexity. However, evolutionary algorithms may get computationally expensive for mathematically well behaved problems with large number of variables for which classical mathematical programming approaches are better suited. In this paper, we demonstrate a decomposition strategy that allows us to synergistically apply two complementary approaches at the same time on a complex optimization problem. Evolutionary algorithms are useful in this context as their flexibility makes pairing with other solution approaches easy. The decomposition idea is a special case of bilevel optimization that separates the difficulties into two levels and assigns different approaches at each level that is better equipped at handling them. We demonstrate the benefits of the proposed decomposition idea on a wide range of test problems.

A Linear Programming Enhanced Genetic Algorithm for Hyperparameter Tuning in Machine Learning

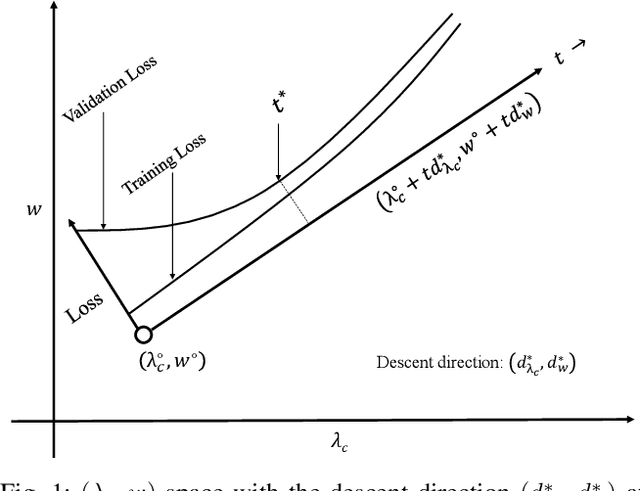
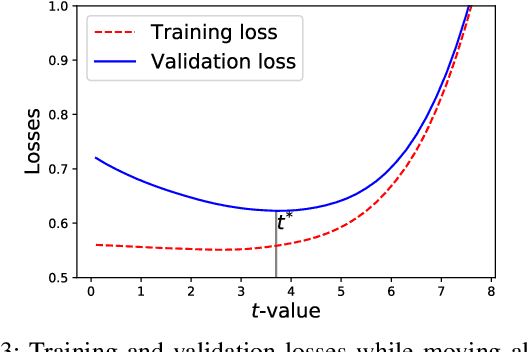
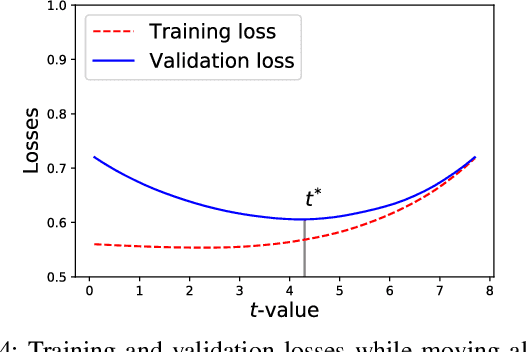
In this paper, we formulate the hyperparameter tuning problem in machine learning as a bilevel program. The bilevel program is solved using a micro genetic algorithm that is enhanced with a linear program. While the genetic algorithm searches over discrete hyperparameters, the linear program enhancement allows hyper local search over continuous hyperparameters. The major contribution in this paper is the formulation of a linear program that supports fast search over continuous hyperparameters, and can be integrated with any hyperparameter search technique. It can also be applied directly on any trained machine learning or deep learning model for the purpose of fine-tuning. We test the performance of the proposed approach on two datasets, MNIST and CIFAR-10. Our results clearly demonstrate that using the linear program enhancement offers significant promise when incorporated with any population-based approach for hyperparameter tuning.

SEntFiN 1.0: Entity-Aware Sentiment Analysis for Financial News

Fine-grained financial sentiment analysis on news headlines is a challenging task requiring human-annotated datasets to achieve high performance. Limited studies have tried to address the sentiment extraction task in a setting where multiple entities are present in a news headline. In an effort to further research in this area, we make publicly available SEntFiN 1.0, a human-annotated dataset of 10,753 news headlines with entity-sentiment annotations, of which 2,847 headlines contain multiple entities, often with conflicting sentiments. We augment our dataset with a database of over 1,000 financial entities and their various representations in news media amounting to over 5,000 phrases. We propose a framework that enables the extraction of entity-relevant sentiments using a feature-based approach rather than an expression-based approach. For sentiment extraction, we utilize 12 different learning schemes utilizing lexicon-based and pre-trained sentence representations and five classification approaches. Our experiments indicate that lexicon-based n-gram ensembles are above par with pre-trained word embedding schemes such as GloVe. Overall, RoBERTa and finBERT (domain-specific BERT) achieve the highest average accuracy of 94.29% and F1-score of 93.27%. Further, using over 210,000 entity-sentiment predictions, we validate the economic effect of sentiments on aggregate market movements over a long duration.

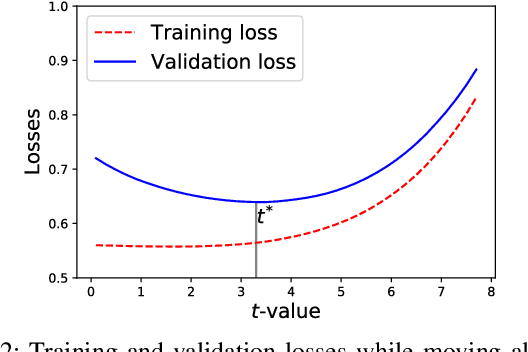
A Globally Convergent Gradient-based Bilevel Hyperparameter Optimization Method

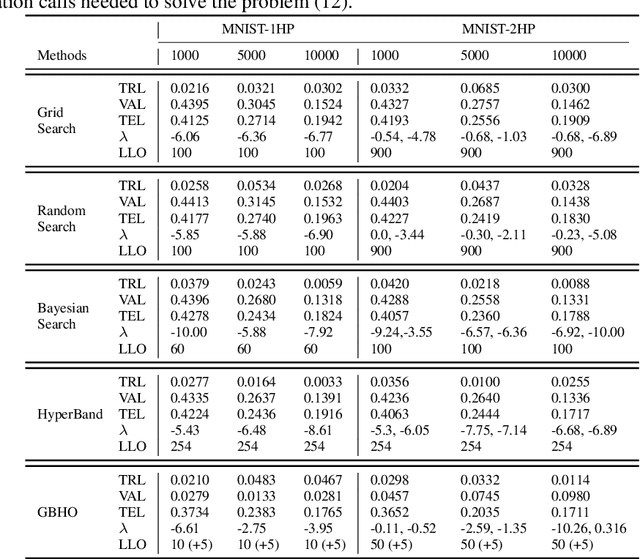
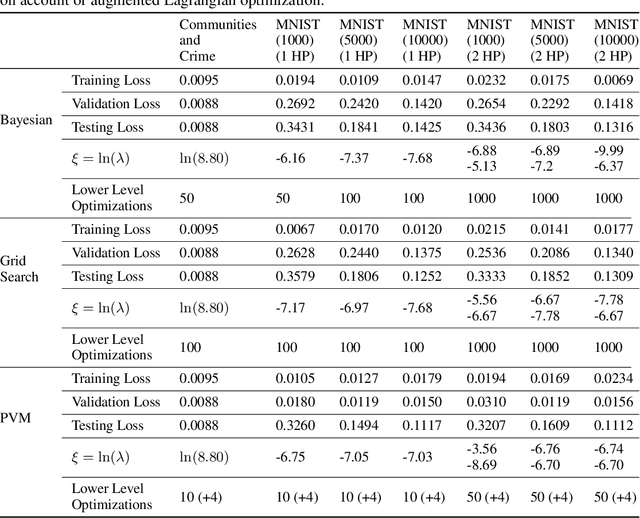
Hyperparameter optimization in machine learning is often achieved using naive techniques that only lead to an approximate set of hyperparameters. Although techniques such as Bayesian optimization perform an intelligent search on a given domain of hyperparameters, it does not guarantee an optimal solution. A major drawback of most of these approaches is an exponential increase of their search domain with number of hyperparameters, increasing the computational cost and making the approaches slow. The hyperparameter optimization problem is inherently a bilevel optimization task, and some studies have attempted bilevel solution methodologies for solving this problem. However, these studies assume a unique set of model weights that minimize the training loss, which is generally violated by deep learning architectures. This paper discusses a gradient-based bilevel method addressing these drawbacks for solving the hyperparameter optimization problem. The proposed method can handle continuous hyperparameters for which we have chosen the regularization hyperparameter in our experiments. The method guarantees convergence to the set of optimal hyperparameters that this study has theoretically proven. The idea is based on approximating the lower-level optimal value function using Gaussian process regression. As a result, the bilevel problem is reduced to a single level constrained optimization task that is solved using the augmented Lagrangian method. We have performed an extensive computational study on the MNIST and CIFAR-10 datasets on multi-layer perceptron and LeNet architectures that confirms the efficiency of the proposed method. A comparative study against grid search, random search, Bayesian optimization, and HyberBand method on various hyperparameter problems shows that the proposed algorithm converges with lower computation and leads to models that generalize better on the testing set.

Impact of News on the Commodity Market: Dataset and Results

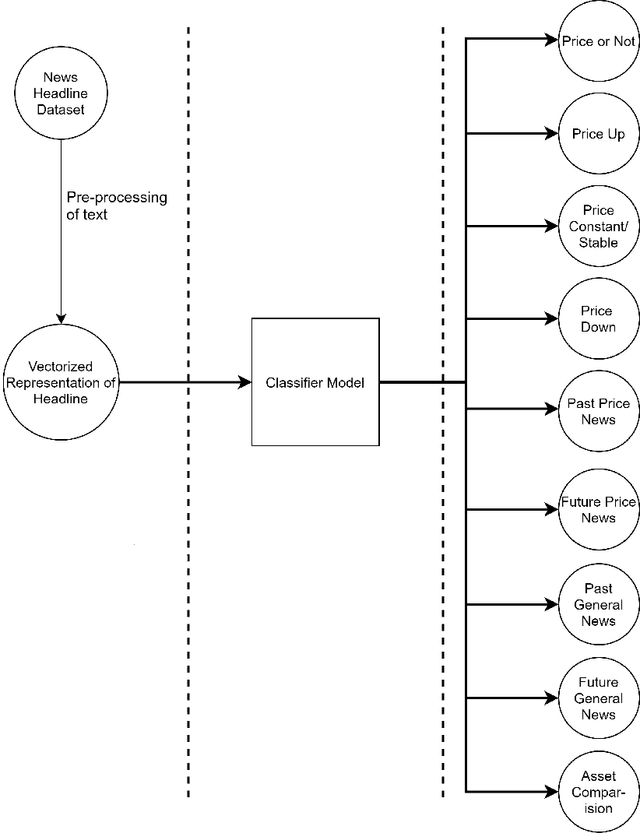
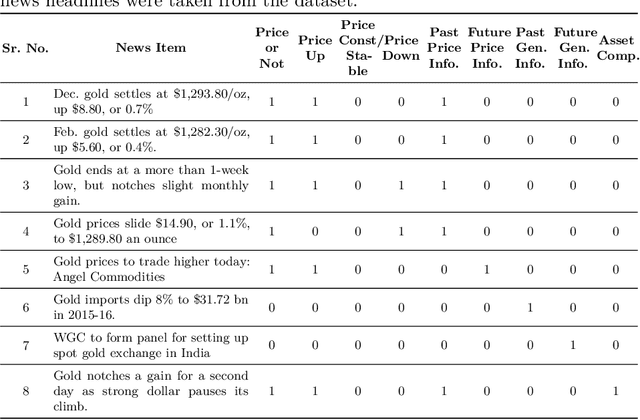
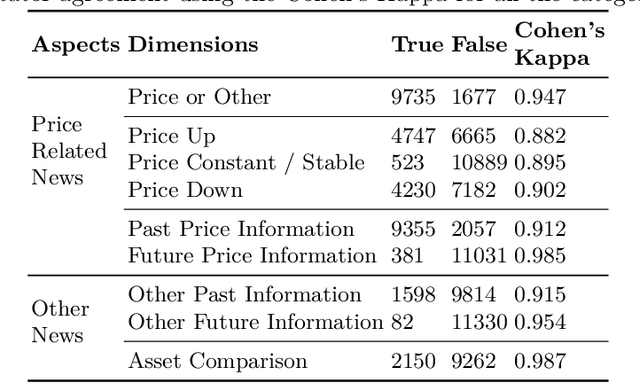
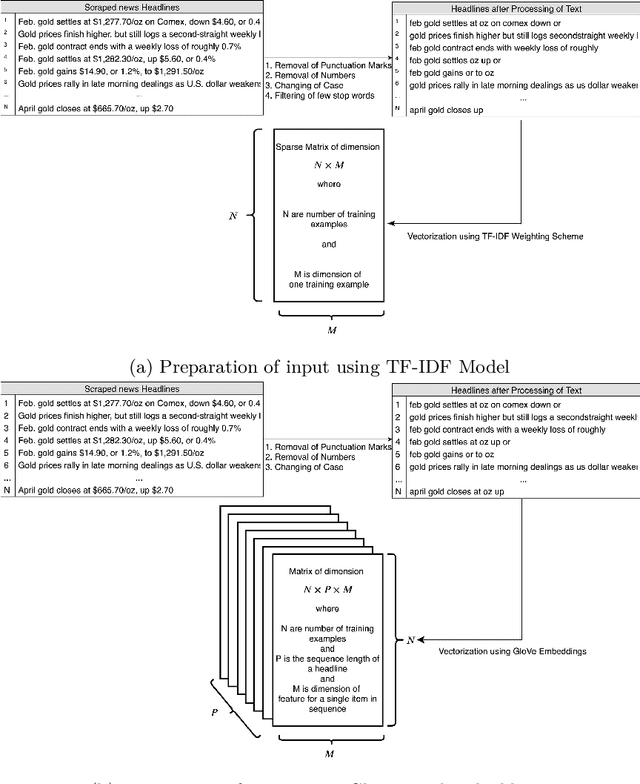
Over the last few years, machine learning based methods have been applied to extract information from news flow in the financial domain. However, this information has mostly been in the form of the financial sentiments contained in the news headlines, primarily for the stock prices. In our current work, we propose that various other dimensions of information can be extracted from news headlines, which will be of interest to investors, policy-makers and other practitioners. We propose a framework that extracts information such as past movements and expected directionality in prices, asset comparison and other general information that the news is referring to. We apply this framework to the commodity "Gold" and train the machine learning models using a dataset of 11,412 human-annotated news headlines (released with this study), collected from the period 2000-2019. We experiment to validate the causal effect of news flow on gold prices and observe that the information produced from our framework significantly impacts the future gold price.

A Gradient-based Bilevel Optimization Approach for Tuning Hyperparameters in Machine Learning

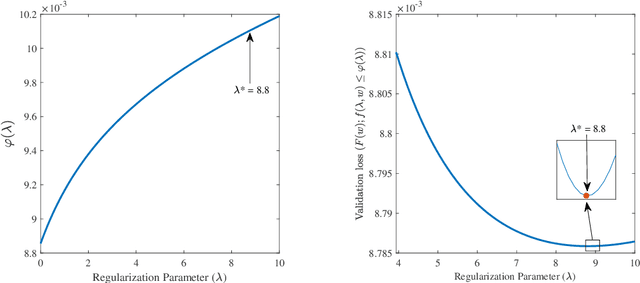
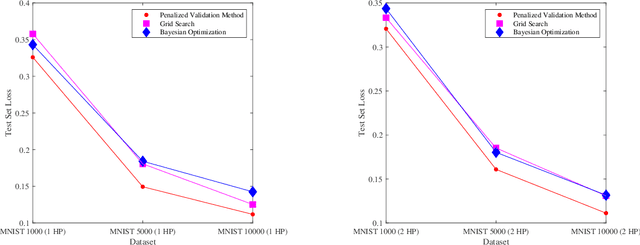
Hyperparameter tuning is an active area of research in machine learning, where the aim is to identify the optimal hyperparameters that provide the best performance on the validation set. Hyperparameter tuning is often achieved using naive techniques, such as random search and grid search. However, most of these methods seldom lead to an optimal set of hyperparameters and often get very expensive. In this paper, we propose a bilevel solution method for solving the hyperparameter optimization problem that does not suffer from the drawbacks of the earlier studies. The proposed method is general and can be easily applied to any class of machine learning algorithms. The idea is based on the approximation of the lower level optimal value function mapping, which is an important mapping in bilevel optimization and helps in reducing the bilevel problem to a single level constrained optimization task. The single-level constrained optimization problem is solved using the augmented Lagrangian method. We discuss the theory behind the proposed algorithm and perform extensive computational study on two datasets that confirm the efficiency of the proposed method. We perform a comparative study against grid search, random search and Bayesian optimization techniques that shows that the proposed algorithm is multiple times faster on problems with one or two hyperparameters. The computational gain is expected to be significantly higher as the number of hyperparameters increase. Corresponding to a given hyperparameter most of the techniques in the literature often assume a unique optimal parameter set that minimizes loss on the training set. Such an assumption is often violated by deep learning architectures and the proposed method does not require any such assumption.

A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications

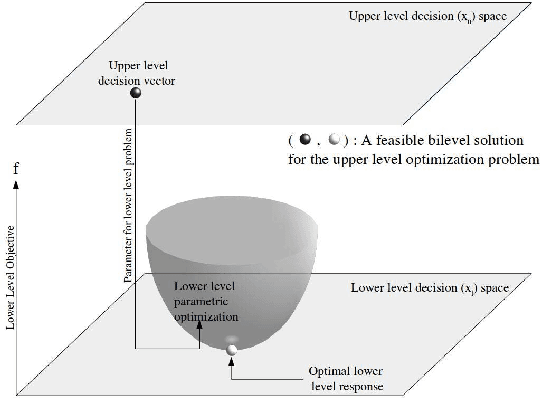
Bilevel optimization is defined as a mathematical program, where an optimization problem contains another optimization problem as a constraint. These problems have received significant attention from the mathematical programming community. Only limited work exists on bilevel problems using evolutionary computation techniques; however, recently there has been an increasing interest due to the proliferation of practical applications and the potential of evolutionary algorithms in tackling these problems. This paper provides a comprehensive review on bilevel optimization from the basic principles to solution strategies; both classical and evolutionary. A number of potential application problems are also discussed. To offer the readers insights on the prominent developments in the field of bilevel optimization, we have performed an automated text-analysis of an extended list of papers published on bilevel optimization to date. This paper should motivate evolutionary computation researchers to pay more attention to this practical yet challenging area.

Optimal Management of Naturally Regenerating Uneven-aged Forests

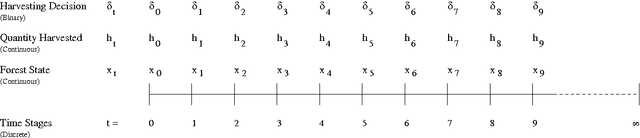
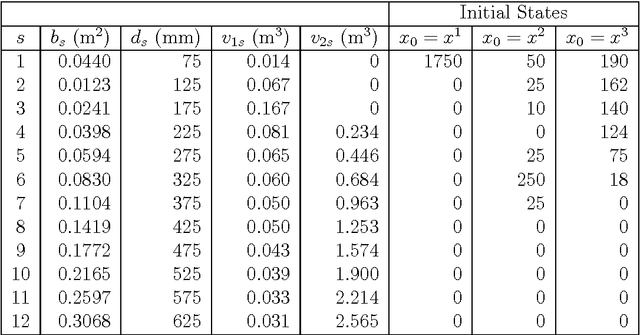
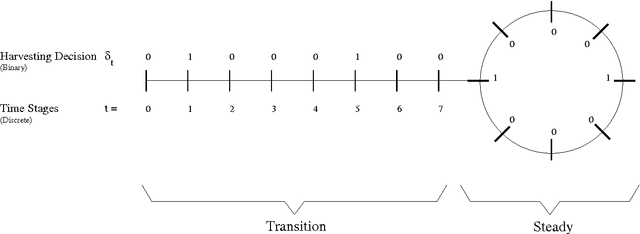
A shift from even-aged forest management to uneven-aged management practices leads to a problem rather different from the existing straightforward practice that follows a rotation cycle of artificial regeneration, thinning of inferior trees and a clearcut. A lack of realistic models and methods suggesting how to manage uneven-aged stands in a way that is economically viable and ecologically sustainable creates difficulties in adopting this new management practice. To tackle this problem, we make a two-fold contribution in this paper. The first contribution is the proposal of an algorithm that is able to handle a realistic uneven-aged stand management model that is otherwise computationally tedious and intractable. The model considered in this paper is an empirically estimated size-structured ecological model for uneven-aged spruce forests. The second contribution is on the sensitivity analysis of the forest model with respect to a number of important parameters. The analysis provides us an insight into the behavior of the uneven-aged forest model.

A Multi-objective Exploratory Procedure for Regression Model Selection

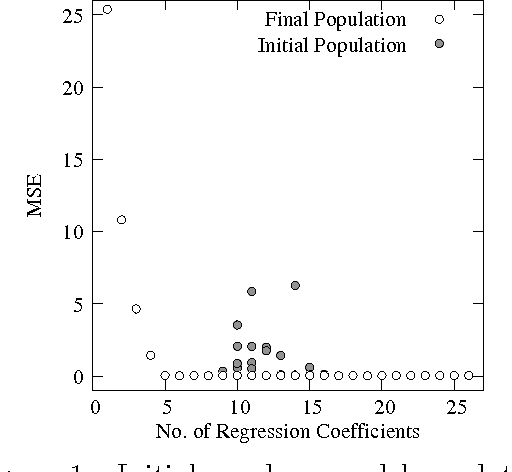
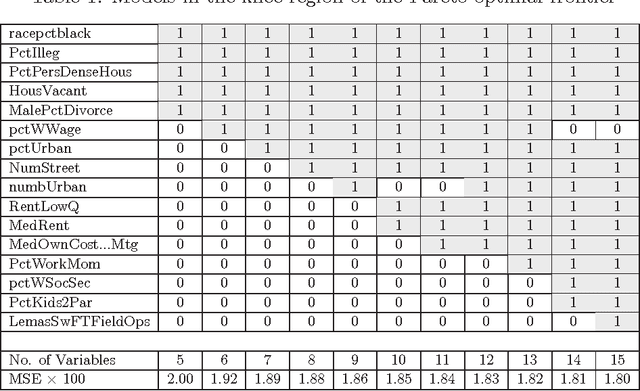
Variable selection is recognized as one of the most critical steps in statistical modeling. The problems encountered in engineering and social sciences are commonly characterized by over-abundance of explanatory variables, non-linearities and unknown interdependencies between the regressors. An added difficulty is that the analysts may have little or no prior knowledge on the relative importance of the variables. To provide a robust method for model selection, this paper introduces the Multi-objective Genetic Algorithm for Variable Selection (MOGA-VS) that provides the user with an optimal set of regression models for a given data-set. The algorithm considers the regression problem as a two objective task, and explores the Pareto-optimal (best subset) models by preferring those models over the other which have less number of regression coefficients and better goodness of fit. The model exploration can be performed based on in-sample or generalization error minimization. The model selection is proposed to be performed in two steps. First, we generate the frontier of Pareto-optimal regression models by eliminating the dominated models without any user intervention. Second, a decision making process is executed which allows the user to choose the most preferred model using visualisations and simple metrics. The method has been evaluated on a recently published real dataset on Communities and Crime within United States.

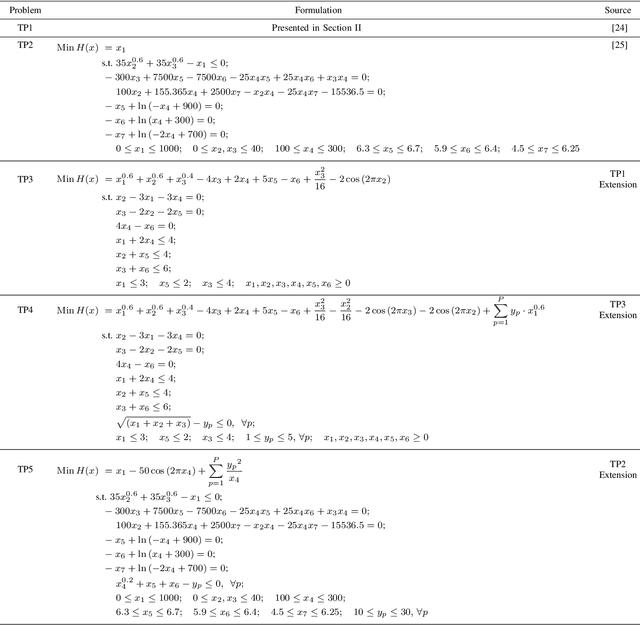
Efficient Evolutionary Algorithm for Single-Objective Bilevel Optimization

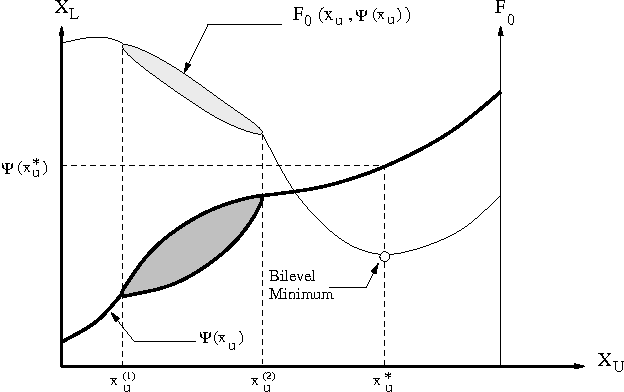
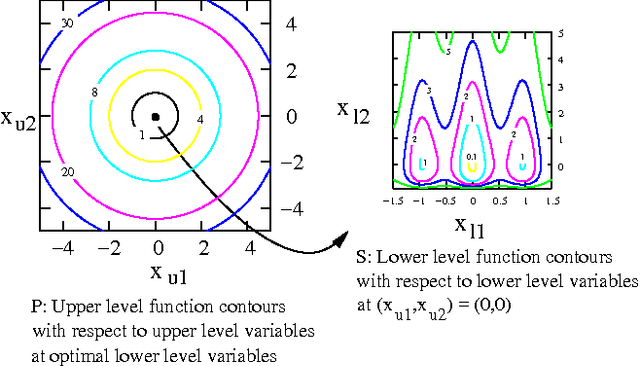
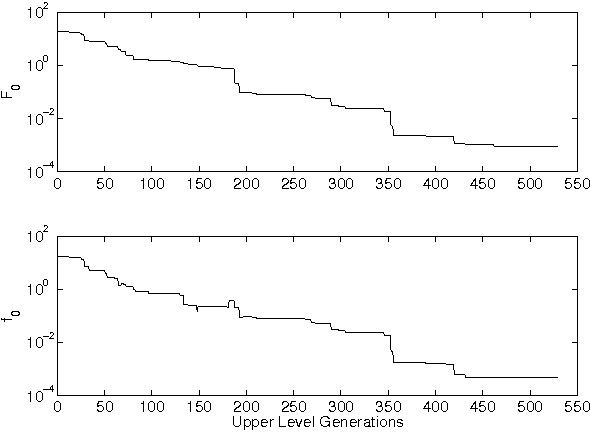
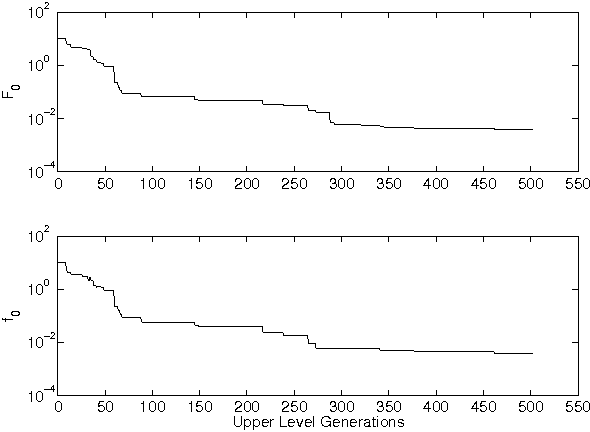
Bilevel optimization problems are a class of challenging optimization problems, which contain two levels of optimization tasks. In these problems, the optimal solutions to the lower level problem become possible feasible candidates to the upper level problem. Such a requirement makes the optimization problem difficult to solve, and has kept the researchers busy towards devising methodologies, which can efficiently handle the problem. Despite the efforts, there hardly exists any effective methodology, which is capable of handling a complex bilevel problem. In this paper, we introduce bilevel evolutionary algorithm based on quadratic approximations (BLEAQ) of optimal lower level variables with respect to the upper level variables. The approach is capable of handling bilevel problems with different kinds of complexities in relatively smaller number of function evaluations. Ideas from classical optimization have been hybridized with evolutionary methods to generate an efficient optimization algorithm for generic bilevel problems. The efficacy of the algorithm has been shown on two sets of test problems. The first set is a recently proposed SMD test set, which contains problems with controllable complexities, and the second set contains standard test problems collected from the literature. The proposed method has been evaluated against two benchmarks, and the performance gain is observed to be significant.