A Globally Convergent Gradient-based Bilevel Hyperparameter Optimization Method
Paper and Code
Aug 25, 2022
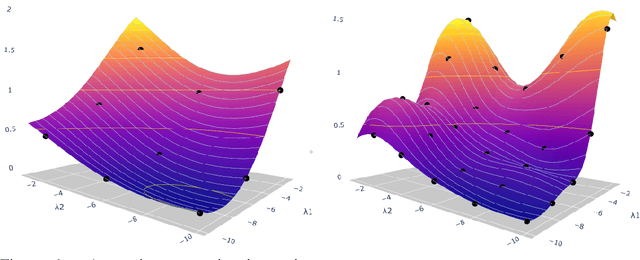
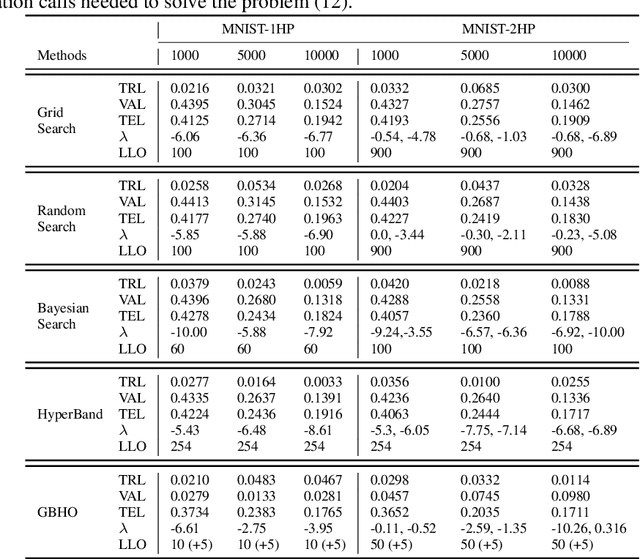

Hyperparameter optimization in machine learning is often achieved using naive techniques that only lead to an approximate set of hyperparameters. Although techniques such as Bayesian optimization perform an intelligent search on a given domain of hyperparameters, it does not guarantee an optimal solution. A major drawback of most of these approaches is an exponential increase of their search domain with number of hyperparameters, increasing the computational cost and making the approaches slow. The hyperparameter optimization problem is inherently a bilevel optimization task, and some studies have attempted bilevel solution methodologies for solving this problem. However, these studies assume a unique set of model weights that minimize the training loss, which is generally violated by deep learning architectures. This paper discusses a gradient-based bilevel method addressing these drawbacks for solving the hyperparameter optimization problem. The proposed method can handle continuous hyperparameters for which we have chosen the regularization hyperparameter in our experiments. The method guarantees convergence to the set of optimal hyperparameters that this study has theoretically proven. The idea is based on approximating the lower-level optimal value function using Gaussian process regression. As a result, the bilevel problem is reduced to a single level constrained optimization task that is solved using the augmented Lagrangian method. We have performed an extensive computational study on the MNIST and CIFAR-10 datasets on multi-layer perceptron and LeNet architectures that confirms the efficiency of the proposed method. A comparative study against grid search, random search, Bayesian optimization, and HyberBand method on various hyperparameter problems shows that the proposed algorithm converges with lower computation and leads to models that generalize better on the testing set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge