Efficient Evolutionary Algorithm for Single-Objective Bilevel Optimization
Paper and Code
Oct 07, 2013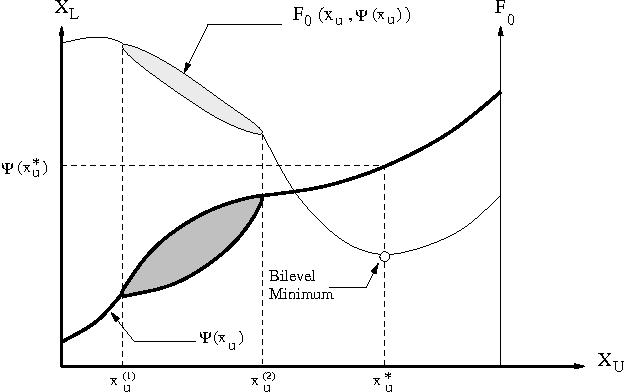
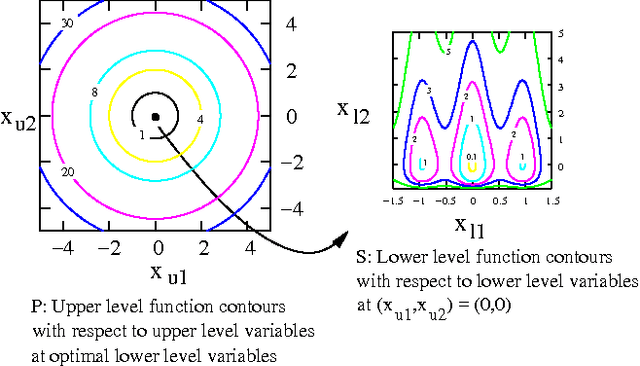
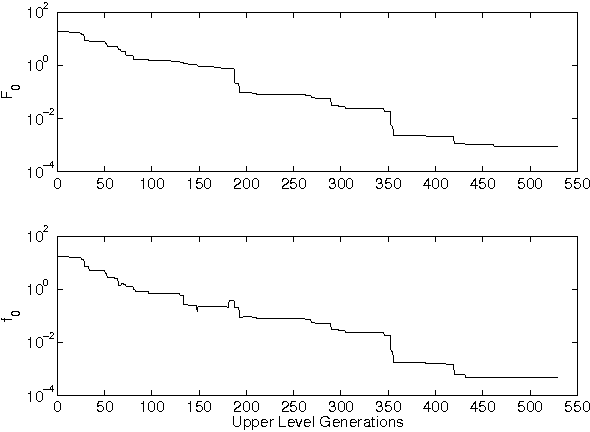
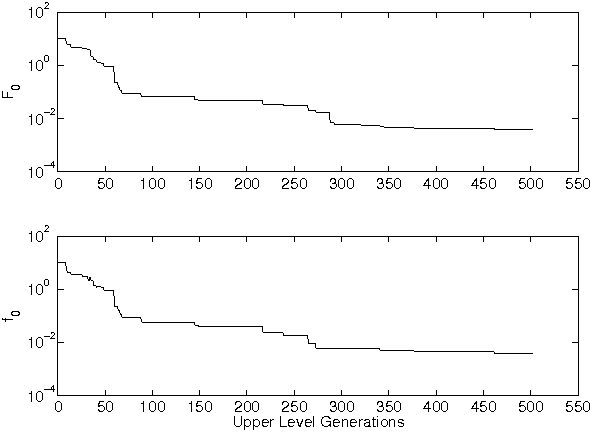
Bilevel optimization problems are a class of challenging optimization problems, which contain two levels of optimization tasks. In these problems, the optimal solutions to the lower level problem become possible feasible candidates to the upper level problem. Such a requirement makes the optimization problem difficult to solve, and has kept the researchers busy towards devising methodologies, which can efficiently handle the problem. Despite the efforts, there hardly exists any effective methodology, which is capable of handling a complex bilevel problem. In this paper, we introduce bilevel evolutionary algorithm based on quadratic approximations (BLEAQ) of optimal lower level variables with respect to the upper level variables. The approach is capable of handling bilevel problems with different kinds of complexities in relatively smaller number of function evaluations. Ideas from classical optimization have been hybridized with evolutionary methods to generate an efficient optimization algorithm for generic bilevel problems. The efficacy of the algorithm has been shown on two sets of test problems. The first set is a recently proposed SMD test set, which contains problems with controllable complexities, and the second set contains standard test problems collected from the literature. The proposed method has been evaluated against two benchmarks, and the performance gain is observed to be significant.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge