A Multi-objective Exploratory Procedure for Regression Model Selection
Paper and Code
Jul 13, 2016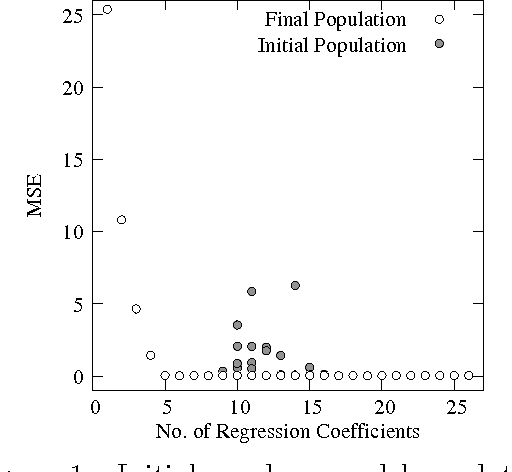
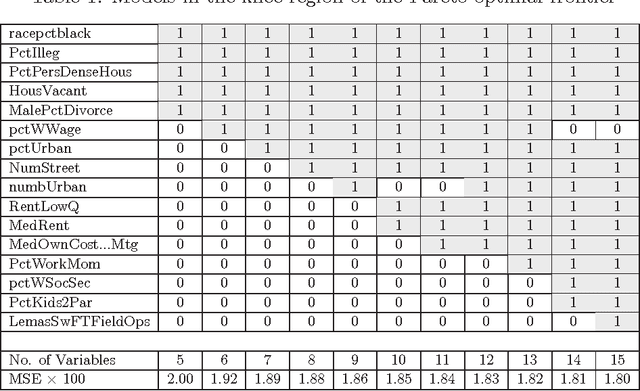
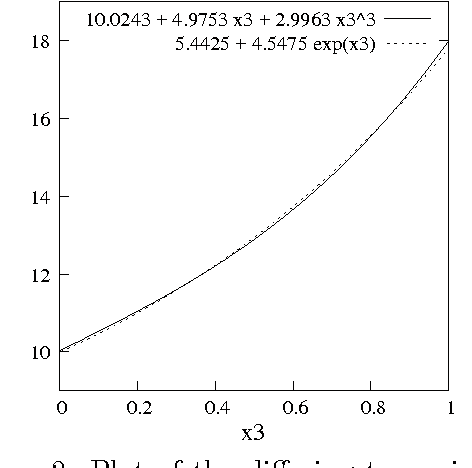

Variable selection is recognized as one of the most critical steps in statistical modeling. The problems encountered in engineering and social sciences are commonly characterized by over-abundance of explanatory variables, non-linearities and unknown interdependencies between the regressors. An added difficulty is that the analysts may have little or no prior knowledge on the relative importance of the variables. To provide a robust method for model selection, this paper introduces the Multi-objective Genetic Algorithm for Variable Selection (MOGA-VS) that provides the user with an optimal set of regression models for a given data-set. The algorithm considers the regression problem as a two objective task, and explores the Pareto-optimal (best subset) models by preferring those models over the other which have less number of regression coefficients and better goodness of fit. The model exploration can be performed based on in-sample or generalization error minimization. The model selection is proposed to be performed in two steps. First, we generate the frontier of Pareto-optimal regression models by eliminating the dominated models without any user intervention. Second, a decision making process is executed which allows the user to choose the most preferred model using visualisations and simple metrics. The method has been evaluated on a recently published real dataset on Communities and Crime within United States.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge