Dhaval Pujara
Decomposition of Difficulties in Complex Optimization Problems Using a Bilevel Approach
Jul 03, 2024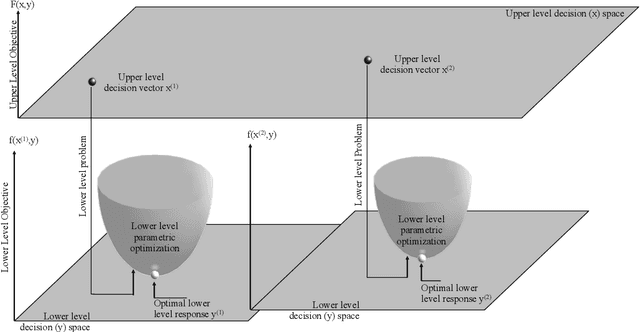
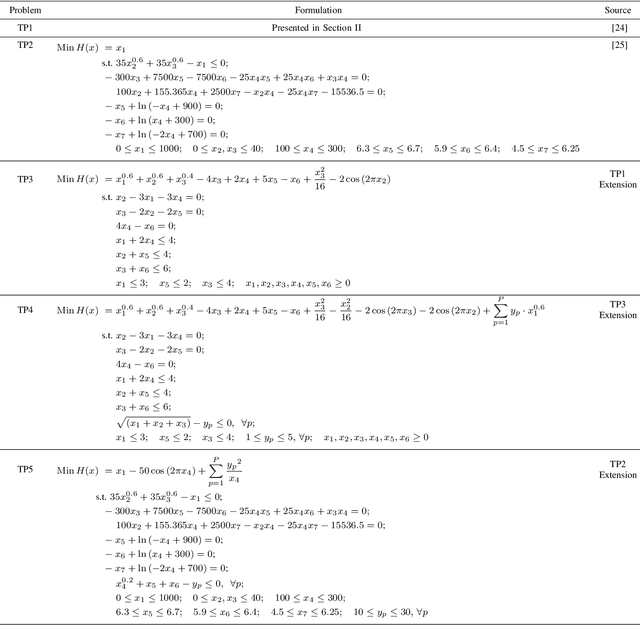


Abstract:Practical optimization problems may contain different kinds of difficulties that are often not tractable if one relies on a particular optimization method. Different optimization approaches offer different strengths that are good at tackling one or more difficulty in an optimization problem. For instance, evolutionary algorithms have a niche in handling complexities like discontinuity, non-differentiability, discreteness and non-convexity. However, evolutionary algorithms may get computationally expensive for mathematically well behaved problems with large number of variables for which classical mathematical programming approaches are better suited. In this paper, we demonstrate a decomposition strategy that allows us to synergistically apply two complementary approaches at the same time on a complex optimization problem. Evolutionary algorithms are useful in this context as their flexibility makes pairing with other solution approaches easy. The decomposition idea is a special case of bilevel optimization that separates the difficulties into two levels and assigns different approaches at each level that is better equipped at handling them. We demonstrate the benefits of the proposed decomposition idea on a wide range of test problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge