A Likelihood Based Approach to Distribution Regression Using Conditional Deep Generative Models
Paper and Code
Oct 02, 2024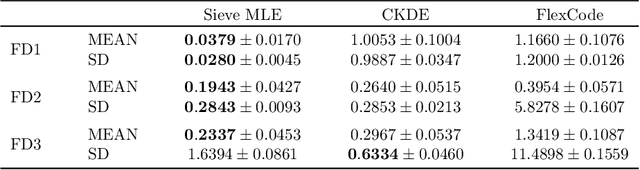
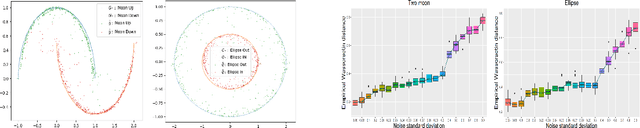

In this work, we explore the theoretical properties of conditional deep generative models under the statistical framework of distribution regression where the response variable lies in a high-dimensional ambient space but concentrates around a potentially lower-dimensional manifold. More specifically, we study the large-sample properties of a likelihood-based approach for estimating these models. Our results lead to the convergence rate of a sieve maximum likelihood estimator (MLE) for estimating the conditional distribution (and its devolved counterpart) of the response given predictors in the Hellinger (Wasserstein) metric. Our rates depend solely on the intrinsic dimension and smoothness of the true conditional distribution. These findings provide an explanation of why conditional deep generative models can circumvent the curse of dimensionality from the perspective of statistical foundations and demonstrate that they can learn a broader class of nearly singular conditional distributions. Our analysis also emphasizes the importance of introducing a small noise perturbation to the data when they are supported sufficiently close to a manifold. Finally, in our numerical studies, we demonstrate the effective implementation of the proposed approach using both synthetic and real-world datasets, which also provide complementary validation to our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge