Schreier-Coset Graph Propagation

Graph Neural Networks (GNNs) offer a principled framework for learning over graph-structured data, yet their expressive capacity is often hindered by over-squashing, wherein information from distant nodes is compressed into fixed-size vectors. Existing solutions, including graph rewiring and bottleneck-resistant architectures such as Cayley and expander graphs, avoid this problem but introduce scalability bottlenecks. In particular, the Cayley graphs constructed over $SL(2,\mathbb{Z}_n)$ exhibit strong theoretical properties, yet suffer from cubic node growth $O(n^3)$, leading to high memory usage. To address this, this work introduces Schrier-Coset Graph Propagation (SCGP), a group-theoretic augmentation method that enriches node features through Schreier-coset embeddings without altering the input graph topology. SCGP embeds bottleneck-free connectivity patterns into a compact feature space, improving long-range message passing while maintaining computational efficiency. Empirical evaluations across standard node and graph classification benchmarks demonstrate that SCGP achieves performance comparable to, or exceeding, expander graph and rewired GNN baselines. Furthermore, SCGP exhibits particular advantages in processing hierarchical and modular graph structures, offering reduced inference latency, improved scalability, and a low memory footprint, making it suitable for real-time and resource-constrained applications.

Robust and Scalable Variational Bayes

We propose a robust and scalable framework for variational Bayes (VB) that effectively handles outliers and contamination of arbitrary nature in large datasets. Our approach divides the dataset into disjoint subsets, computes the posterior for each subset, and applies VB approximation independently to these posteriors. The resulting variational posteriors with respect to the subsets are then aggregated using the geometric median of probability measures, computed with respect to the Wasserstein distance. This novel aggregation method yields the Variational Median Posterior (VM-Posterior) distribution. We rigorously demonstrate that the VM-Posterior preserves contraction properties akin to those of the true posterior, while accounting for approximation errors or the variational gap inherent in VB methods. We also provide provable robustness guarantee of the VM-Posterior. Furthermore, we establish a variational Bernstein-von Mises theorem for both multivariate Gaussian distributions with general covariance structures and the mean-field variational family. To facilitate practical implementation, we adapt existing algorithms for computing the VM-Posterior and evaluate its performance through extensive numerical experiments. The results highlight its robustness and scalability, making it a reliable tool for Bayesian inference in the presence of complex, contaminated datasets.

A Likelihood Based Approach to Distribution Regression Using Conditional Deep Generative Models

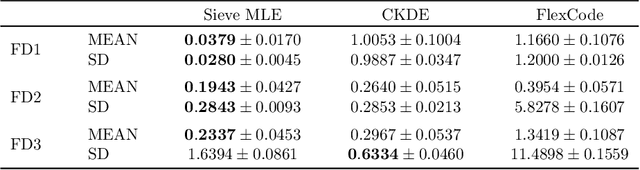
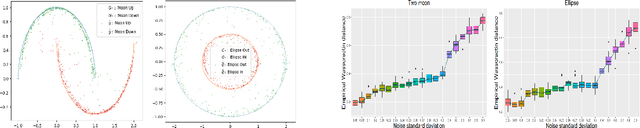
In this work, we explore the theoretical properties of conditional deep generative models under the statistical framework of distribution regression where the response variable lies in a high-dimensional ambient space but concentrates around a potentially lower-dimensional manifold. More specifically, we study the large-sample properties of a likelihood-based approach for estimating these models. Our results lead to the convergence rate of a sieve maximum likelihood estimator (MLE) for estimating the conditional distribution (and its devolved counterpart) of the response given predictors in the Hellinger (Wasserstein) metric. Our rates depend solely on the intrinsic dimension and smoothness of the true conditional distribution. These findings provide an explanation of why conditional deep generative models can circumvent the curse of dimensionality from the perspective of statistical foundations and demonstrate that they can learn a broader class of nearly singular conditional distributions. Our analysis also emphasizes the importance of introducing a small noise perturbation to the data when they are supported sufficiently close to a manifold. Finally, in our numerical studies, we demonstrate the effective implementation of the proposed approach using both synthetic and real-world datasets, which also provide complementary validation to our theoretical findings.

Nested stochastic block model for simultaneously clustering networks and nodes

We introduce the nested stochastic block model (NSBM) to cluster a collection of networks while simultaneously detecting communities within each network. NSBM has several appealing features including the ability to work on unlabeled networks with potentially different node sets, the flexibility to model heterogeneous communities, and the means to automatically select the number of classes for the networks and the number of communities within each network. This is accomplished via a Bayesian model, with a novel application of the nested Dirichlet process (NDP) as a prior to jointly model the between-network and within-network clusters. The dependency introduced by the network data creates nontrivial challenges for the NDP, especially in the development of efficient samplers. For posterior inference, we propose several Markov chain Monte Carlo algorithms including a standard Gibbs sampler, a collapsed Gibbs sampler, and two blocked Gibbs samplers that ultimately return two levels of clustering labels from both within and across the networks. Extensive simulation studies are carried out which demonstrate that the model provides very accurate estimates of both levels of the clustering structure. We also apply our model to two social network datasets that cannot be analyzed using any previous method in the literature due to the anonymity of the nodes and the varying number of nodes in each network.

A Bayesian sparse factor model with adaptive posterior concentration

In this paper, we propose a new Bayesian inference method for a high-dimensional sparse factor model that allows both the factor dimensionality and the sparse structure of the loading matrix to be inferred. The novelty is to introduce a certain dependence between the sparsity level and the factor dimensionality, which leads to adaptive posterior concentration while keeping computational tractability. We show that the posterior distribution asymptotically concentrates on the true factor dimensionality, and more importantly, this posterior consistency is adaptive to the sparsity level of the true loading matrix and the noise variance. We also prove that the proposed Bayesian model attains the optimal detection rate of the factor dimensionality in a more general situation than those found in the literature. Moreover, we obtain a near-optimal posterior concentration rate of the covariance matrix. Numerical studies are conducted and show the superiority of the proposed method compared with other competitors.

Machine Learning and the Future of Bayesian Computation

Bayesian models are a powerful tool for studying complex data, allowing the analyst to encode rich hierarchical dependencies and leverage prior information. Most importantly, they facilitate a complete characterization of uncertainty through the posterior distribution. Practical posterior computation is commonly performed via MCMC, which can be computationally infeasible for high dimensional models with many observations. In this article we discuss the potential to improve posterior computation using ideas from machine learning. Concrete future directions are explored in vignettes on normalizing flows, Bayesian coresets, distributed Bayesian inference, and variational inference.

A Semi-Bayesian Nonparametric Hypothesis Test Using Maximum Mean Discrepancy with Applications in Generative Adversarial Networks

A classic inferential problem in statistics is the two-sample hypothesis test, where we test whether two samples of observations are either drawn from the same distribution or two distinct distributions. However, standard methods for performing this test require strong distributional assumptions on the two samples of data. We propose a semi-Bayesian nonparametric (semi-BNP) procedure for the two-sample hypothesis testing problem. First, we will derive a novel BNP maximum mean discrepancy (MMD) measure-based hypothesis test. Next, we will show that our proposed test will outperform frequentist MMD-based methods by yielding a smaller false rejection and acceptance rate of the null. Finally, we will show that we can embed our proposed hypothesis testing procedure within a generative adversarial network (GAN) framework as an application of our method. Using our novel BNP hypothesis test, this new GAN approach can help to mitigate the lack of diversity in the generated samples and produce a more accurate inferential algorithm compared to traditional techniques.

Intrinsic and extrinsic deep learning on manifolds

We propose extrinsic and intrinsic deep neural network architectures as general frameworks for deep learning on manifolds. Specifically, extrinsic deep neural networks (eDNNs) preserve geometric features on manifolds by utilizing an equivariant embedding from the manifold to its image in the Euclidean space. Moreover, intrinsic deep neural networks (iDNNs) incorporate the underlying intrinsic geometry of manifolds via exponential and log maps with respect to a Riemannian structure. Consequently, we prove that the empirical risk of the empirical risk minimizers (ERM) of eDNNs and iDNNs converge in optimal rates. Overall, The eDNNs framework is simple and easy to compute, while the iDNNs framework is accurate and fast converging. To demonstrate the utilities of our framework, various simulation studies, and real data analyses are presented with eDNNs and iDNNs.

Extrinsic Bayesian Optimizations on Manifolds

We propose an extrinsic Bayesian optimization (eBO) framework for general optimization problems on manifolds. Bayesian optimization algorithms build a surrogate of the objective function by employing Gaussian processes and quantify the uncertainty in that surrogate by deriving an acquisition function. This acquisition function represents the probability of improvement based on the kernel of the Gaussian process, which guides the search in the optimization process. The critical challenge for designing Bayesian optimization algorithms on manifolds lies in the difficulty of constructing valid covariance kernels for Gaussian processes on general manifolds. Our approach is to employ extrinsic Gaussian processes by first embedding the manifold onto some higher dimensional Euclidean space via equivariant embeddings and then constructing a valid covariance kernel on the image manifold after the embedding. This leads to efficient and scalable algorithms for optimization over complex manifolds. Simulation study and real data analysis are carried out to demonstrate the utilities of our eBO framework by applying the eBO to various optimization problems over manifolds such as the sphere, the Grassmannian, and the manifold of positive definite matrices.

Bayesian community detection for networks with covariates

The increasing prevalence of network data in a vast variety of fields and the need to extract useful information out of them have spurred fast developments in related models and algorithms. Among the various learning tasks with network data, community detection, the discovery of node clusters or "communities," has arguably received the most attention in the scientific community. In many real-world applications, the network data often come with additional information in the form of node or edge covariates that should ideally be leveraged for inference. In this paper, we add to a limited literature on community detection for networks with covariates by proposing a Bayesian stochastic block model with a covariate-dependent random partition prior. Under our prior, the covariates are explicitly expressed in specifying the prior distribution on the cluster membership. Our model has the flexibility of modeling uncertainties of all the parameter estimates including the community membership. Importantly, and unlike the majority of existing methods, our model has the ability to learn the number of the communities via posterior inference without having to assume it to be known. Our model can be applied to community detection in both dense and sparse networks, with both categorical and continuous covariates, and our MCMC algorithm is very efficient with good mixing properties. We demonstrate the superior performance of our model over existing models in a comprehensive simulation study and an application to two real datasets.