Robust and Scalable Variational Bayes

We propose a robust and scalable framework for variational Bayes (VB) that effectively handles outliers and contamination of arbitrary nature in large datasets. Our approach divides the dataset into disjoint subsets, computes the posterior for each subset, and applies VB approximation independently to these posteriors. The resulting variational posteriors with respect to the subsets are then aggregated using the geometric median of probability measures, computed with respect to the Wasserstein distance. This novel aggregation method yields the Variational Median Posterior (VM-Posterior) distribution. We rigorously demonstrate that the VM-Posterior preserves contraction properties akin to those of the true posterior, while accounting for approximation errors or the variational gap inherent in VB methods. We also provide provable robustness guarantee of the VM-Posterior. Furthermore, we establish a variational Bernstein-von Mises theorem for both multivariate Gaussian distributions with general covariance structures and the mean-field variational family. To facilitate practical implementation, we adapt existing algorithms for computing the VM-Posterior and evaluate its performance through extensive numerical experiments. The results highlight its robustness and scalability, making it a reliable tool for Bayesian inference in the presence of complex, contaminated datasets.

Confidence Interval Construction and Conditional Variance Estimation with Dense ReLU Networks

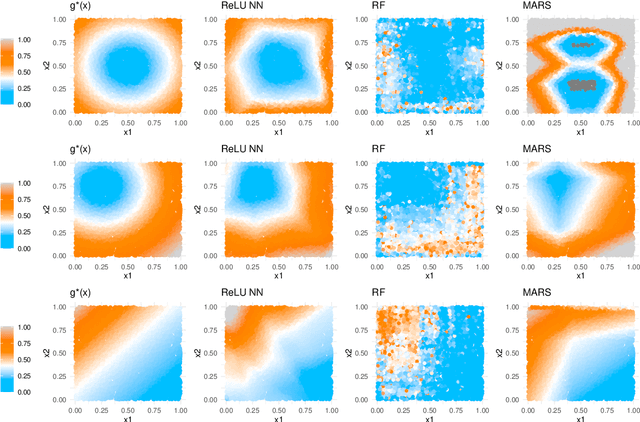
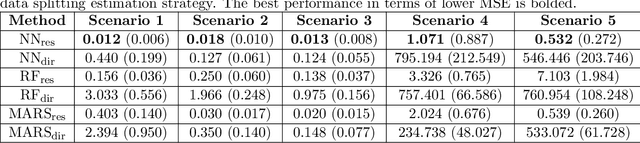
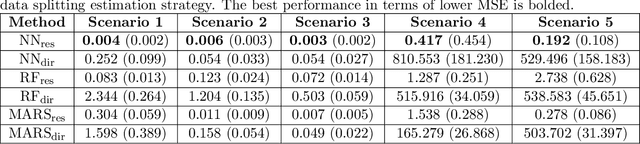
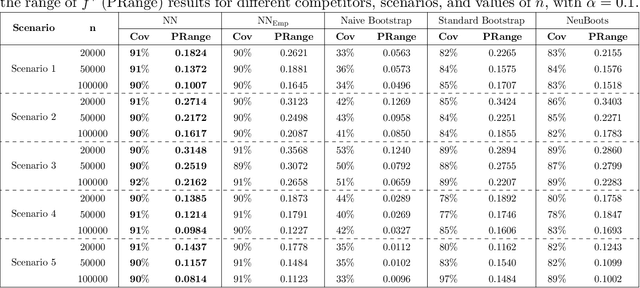
This paper addresses the problems of conditional variance estimation and confidence interval construction in nonparametric regression using dense networks with the Rectified Linear Unit (ReLU) activation function. We present a residual-based framework for conditional variance estimation, deriving nonasymptotic bounds for variance estimation under both heteroscedastic and homoscedastic settings. We relax the sub-Gaussian noise assumption, allowing the proposed bounds to accommodate sub-Exponential noise and beyond. Building on this, for a ReLU neural network estimator, we derive non-asymptotic bounds for both its conditional mean and variance estimation, representing the first result for variance estimation using ReLU networks. Furthermore, we develop a ReLU network based robust bootstrap procedure (Efron, 1992) for constructing confidence intervals for the true mean that comes with a theoretical guarantee on the coverage, providing a significant advancement in uncertainty quantification and the construction of reliable confidence intervals in deep learning settings.

Dense ReLU Neural Networks for Temporal-spatial Model

In this paper, we focus on fully connected deep neural networks utilizing the Rectified Linear Unit (ReLU) activation function for nonparametric estimation. We derive non-asymptotic bounds that lead to convergence rates, addressing both temporal and spatial dependence in the observed measurements. By accounting for dependencies across time and space, our models better reflect the complexities of real-world data, enhancing both predictive performance and theoretical robustness. We also tackle the curse of dimensionality by modeling the data on a manifold, exploring the intrinsic dimensionality of high-dimensional data. We broaden existing theoretical findings of temporal-spatial analysis by applying them to neural networks in more general contexts and demonstrate that our proof techniques are effective for models with short-range dependence. Our empirical simulations across various synthetic response functions underscore the superior performance of our method, outperforming established approaches in the existing literature. These findings provide valuable insights into the strong capabilities of dense neural networks for temporal-spatial modeling across a broad range of function classes.

Temporal-spatial model via Trend Filtering

This research focuses on the estimation of a non-parametric regression function designed for data with simultaneous time and space dependencies. In such a context, we study the Trend Filtering, a nonparametric estimator introduced by \cite{mammen1997locally} and \cite{rudin1992nonlinear}. For univariate settings, the signals we consider are assumed to have a kth weak derivative with bounded total variation, allowing for a general degree of smoothness. In the multivariate scenario, we study a $K$-Nearest Neighbor fused lasso estimator as in \cite{padilla2018adaptive}, employing an ADMM algorithm, suitable for signals with bounded variation that adhere to a piecewise Lipschitz continuity criterion. By aligning with lower bounds, the minimax optimality of our estimators is validated. A unique phase transition phenomenon, previously uncharted in Trend Filtering studies, emerges through our analysis. Both Simulation studies and real data applications underscore the superior performance of our method when compared with established techniques in the existing literature.