Confidence Interval Construction and Conditional Variance Estimation with Dense ReLU Networks
Paper and Code
Dec 29, 2024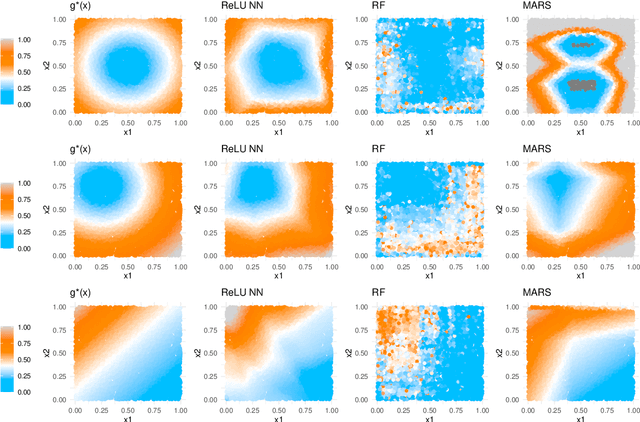
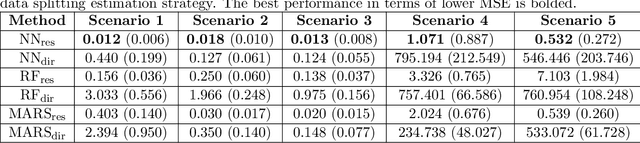
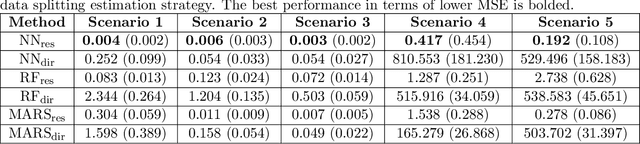
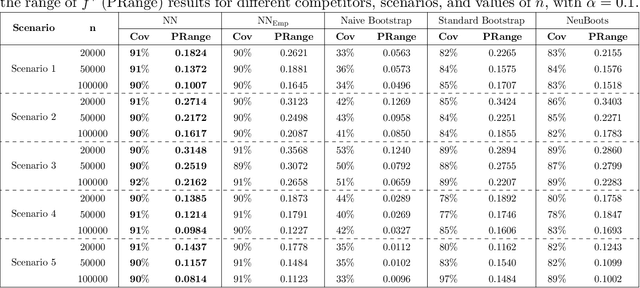
This paper addresses the problems of conditional variance estimation and confidence interval construction in nonparametric regression using dense networks with the Rectified Linear Unit (ReLU) activation function. We present a residual-based framework for conditional variance estimation, deriving nonasymptotic bounds for variance estimation under both heteroscedastic and homoscedastic settings. We relax the sub-Gaussian noise assumption, allowing the proposed bounds to accommodate sub-Exponential noise and beyond. Building on this, for a ReLU neural network estimator, we derive non-asymptotic bounds for both its conditional mean and variance estimation, representing the first result for variance estimation using ReLU networks. Furthermore, we develop a ReLU network based robust bootstrap procedure (Efron, 1992) for constructing confidence intervals for the true mean that comes with a theoretical guarantee on the coverage, providing a significant advancement in uncertainty quantification and the construction of reliable confidence intervals in deep learning settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge