Confidence Interval Construction and Conditional Variance Estimation with Dense ReLU Networks

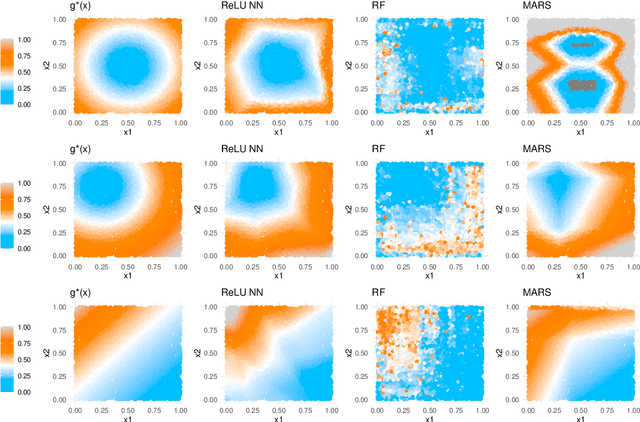
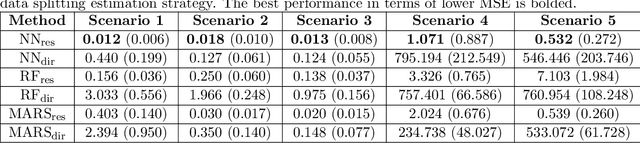
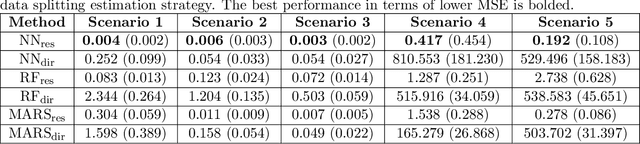
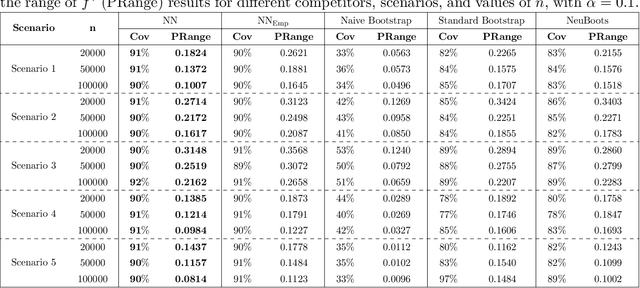
This paper addresses the problems of conditional variance estimation and confidence interval construction in nonparametric regression using dense networks with the Rectified Linear Unit (ReLU) activation function. We present a residual-based framework for conditional variance estimation, deriving nonasymptotic bounds for variance estimation under both heteroscedastic and homoscedastic settings. We relax the sub-Gaussian noise assumption, allowing the proposed bounds to accommodate sub-Exponential noise and beyond. Building on this, for a ReLU neural network estimator, we derive non-asymptotic bounds for both its conditional mean and variance estimation, representing the first result for variance estimation using ReLU networks. Furthermore, we develop a ReLU network based robust bootstrap procedure (Efron, 1992) for constructing confidence intervals for the true mean that comes with a theoretical guarantee on the coverage, providing a significant advancement in uncertainty quantification and the construction of reliable confidence intervals in deep learning settings.

SIRe-IR: Inverse Rendering for BRDF Reconstruction with Shadow and Illumination Removal in High-Illuminance Scenes

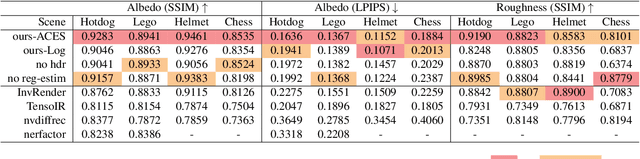
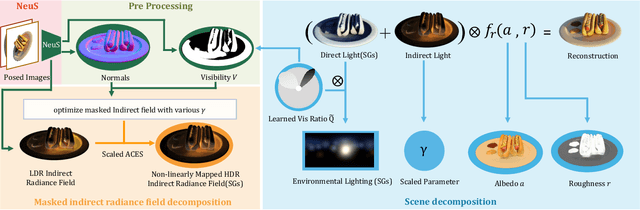
Implicit neural representation has opened up new possibilities for inverse rendering. However, existing implicit neural inverse rendering methods struggle to handle strongly illuminated scenes with significant shadows and indirect illumination. The existence of shadows and reflections can lead to an inaccurate understanding of scene geometry, making precise factorization difficult. To this end, we present SIRe-IR, an implicit neural inverse rendering approach that uses non-linear mapping and regularized visibility estimation to decompose the scene into environment map, albedo, and roughness. By accurately modeling the indirect radiance field, normal, visibility, and direct light simultaneously, we are able to remove both shadows and indirect illumination in materials without imposing strict constraints on the scene. Even in the presence of intense illumination, our method recovers high-quality albedo and roughness with no shadow interference. SIRe-IR outperforms existing methods in both quantitative and qualitative evaluations.

Quantile regression with ReLU Networks: Estimators and minimax rates

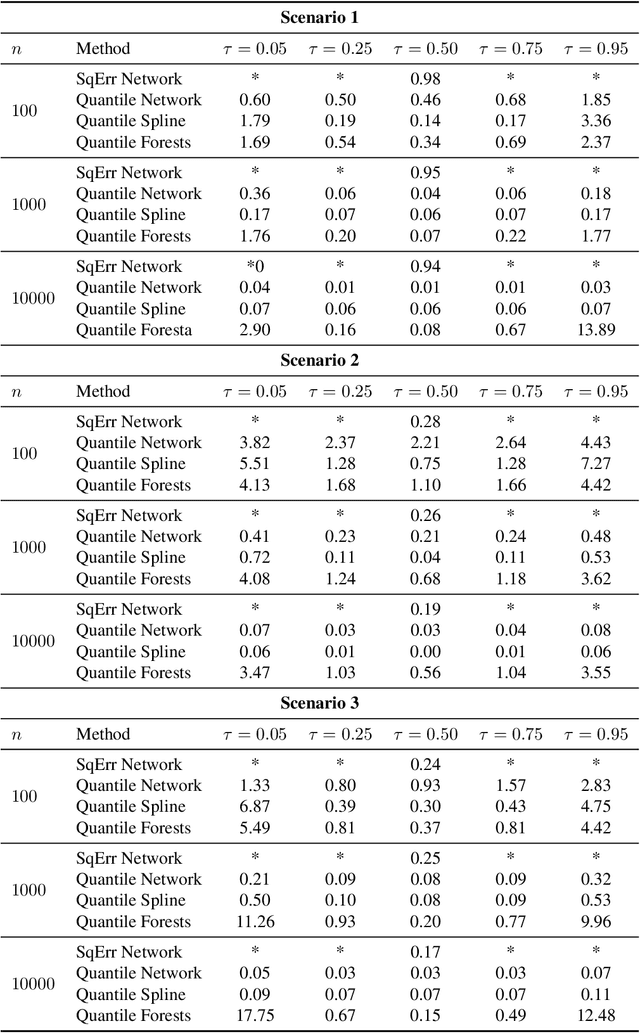
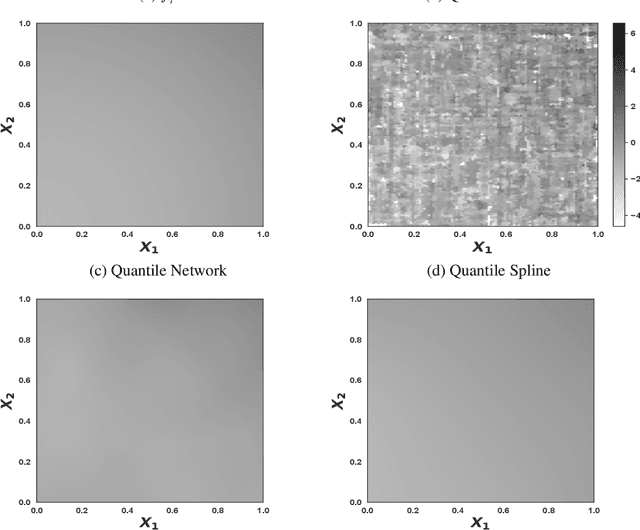
Quantile regression is the task of estimating a specified percentile response, such as the median, from a collection of known covariates. We study quantile regression with rectified linear unit (ReLU) neural networks as the chosen model class. We derive an upper bound on the expected mean squared error of a ReLU network used to estimate any quantile conditional on a set of covariates. This upper bound only depends on the best possible approximation error, the number of layers in the network, and the number of nodes per layer. We further show upper bounds that are tight for two large classes of functions: compositions of H\"older functions and members of a Besov space. These tight bounds imply ReLU networks with quantile regression achieve minimax rates for broad collections of function types. Unlike existing work, the theoretical results hold under minimal assumptions and apply to general error distributions, including heavy-tailed distributions. Empirical simulations on a suite of synthetic response functions demonstrate the theoretical results translate to practical implementations of ReLU networks. Overall, the theoretical and empirical results provide insight into the strong performance of ReLU neural networks for quantile regression across a broad range of function classes and error distributions. All code for this paper is publicly available at https://github.com/tansey/quantile-regression.