HH-PIM: Dynamic Optimization of Power and Performance with Heterogeneous-Hybrid PIM for Edge AI Devices

Processing-in-Memory (PIM) architectures offer promising solutions for efficiently handling AI applications in energy-constrained edge environments. While traditional PIM designs enhance performance and energy efficiency by reducing data movement between memory and processing units, they are limited in edge devices due to continuous power demands and the storage requirements of large neural network weights in SRAM and DRAM. Hybrid PIM architectures, incorporating non-volatile memories like MRAM and ReRAM, mitigate these limitations but struggle with a mismatch between fixed computing resources and dynamically changing inference workloads. To address these challenges, this study introduces a Heterogeneous-Hybrid PIM (HH-PIM) architecture, comprising high-performance MRAM-SRAM PIM modules and low-power MRAM-SRAM PIM modules. We further propose a data placement optimization algorithm that dynamically allocates data based on computational demand, maximizing energy efficiency. FPGA prototyping and power simulations with processors featuring HH-PIM and other PIM types demonstrate that the proposed HH-PIM achieves up to $60.43$ percent average energy savings over conventional PIMs while meeting application latency requirements. These results confirm the suitability of HH-PIM for adaptive, energy-efficient AI processing in edge devices.

Asymptotic Properties for Bayesian Neural Network in Besov Space

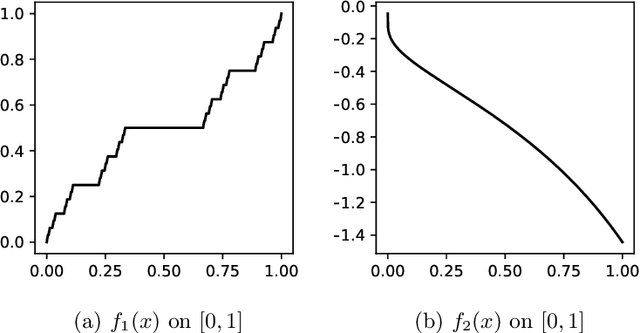
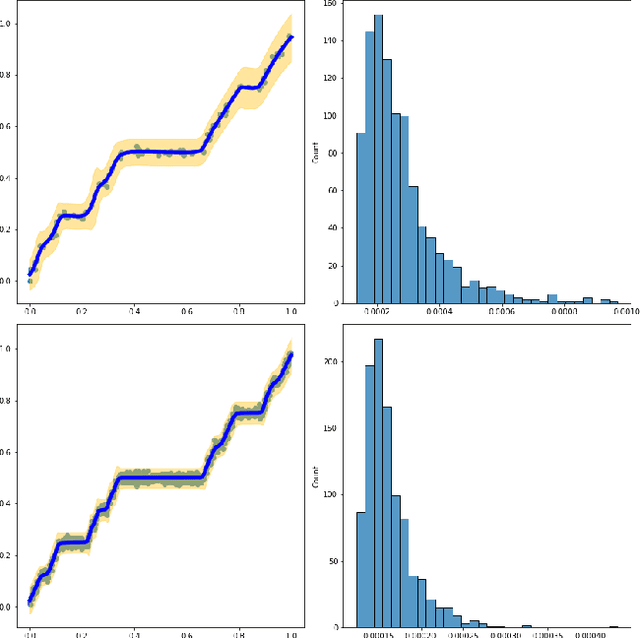
Neural networks have shown great predictive power when dealing with various unstructured data such as images and natural languages. The Bayesian neural network captures the uncertainty of prediction by putting a prior distribution for the parameter of the model and computing the posterior distribution. In this paper, we show that the Bayesian neural network using spike-and-slab prior has consistency with nearly minimax convergence rate when the true regression function is in the Besov space. Even when the smoothness of the regression function is unknown the same posterior convergence rate holds and thus the spike and slab prior is adaptive to the smoothness of the regression function. We also consider the shrinkage prior and show that it has the same convergence rate. In other words, we propose a practical Bayesian neural network with guaranteed asymptotic properties.