Progressive Alignment Objectives for Aligner-Encoder based ASR

Aligner-Encoders are recently proposed seq2seq end-to-end ASR models that replace decoder attention by predicting the uth token directly from the u-th encoder position, so the encoder must learn the alignment internally without cross-attention or a transducer lattice. In practice, this alignment often forms abruptly in the upper layers, making training sensitive and brittle on long utterances. We propose InterAligner, which adds an intermediate Aligner objective so alignment can form progressively across depth, together with an intermediate CTC loss (InterCTC) to stabilize optimization. On LibriSpeech with a 17-layer Conformer, a final-only Aligner reaches 5.0/7.8 WER (test-clean/other). InterCTC improves to 3.4/6.0, and InterAligner further reduces WER to 3.1/5.6 with the largest gains on long utterances.

Posterior Contraction of Lévy Adaptive B-spline Regression in Besov Spaces

We investigate the asymptotic properties of the Lévy Adaptive B-spline (LABS) regression model, a Bayesian nonparametric method that incorporates B-spline kernels into the Lévy Adaptive Regression Kernel (LARK) model. LABS applies splines of varying degrees with independently defined knots, yielding a flexible model class capable of adapting to irregular and locally structured features of the true function. Within the nonparametric regression framework with univariate random design and Gaussian errors, we establish that the LABS posterior contracts around the true function in Besov classes at nearly minimax-optimal rates, up to a logarithmic factor, while adapting automatically to unknown smoothness. This study contributes to filling a gap in the literature, where theoretical results on posterior contraction of the LARK model in Besov spaces remain scarce. Simulation experiments on standard test functions in Besov spaces, including Blocks, Bumps, HeaviSine, and Doppler, complement the theoretical results and demonstrate the practical utility of LABS.

Posterior Contraction Rates for Sparse Kolmogorov-Arnold Networks in Anisotropic Besov Spaces

We study posterior contraction rates for sparse Bayesian Kolmogorov-Arnold networks (KANs) over anisotropic Besov spaces, providing a statistical foundation of KANs from a Bayesian point of view. We show that sparse Bayesian KANs equipped with spike-and-slab-type sparsity priors attain the near-minimax posterior contraction. In particular, the contraction rate depends on the intrinsic anisotropic smoothness of the underlying function. Moreover, by placing a hyperprior on a single model-size parameter, the resulting posterior adapts to unknown anisotropic smoothness and still achieves the corresponding near-minimax rate. A distinctive feature of our results, compared with those for standard sparse MLP-based models, is that the KAN depth can be kept fixed: owing to the flexibility of learnable spline edge functions, the required approximation complexity is controlled through the network width, spline-grid range and size, and parameter sparsity. Our analysis develops theoretical tools tailored to sparse spline-edge architectures, including approximation and complexity bounds for Bayesian KANs. We then extend to compositional Besov spaces and show that the contraction rates depend on layerwise smoothness and effective dimension of the underlying compositional structure, thereby effectively avoiding the curse of dimensionality. Together, the developed tools and findings advance the theoretical understanding of Bayesian neural networks and provide rigorous statistical foundations for KANs.

Pedagogy-R1: Pedagogically-Aligned Reasoning Model with Balanced Educational Benchmark

Recent advances in large reasoning models (LRMs) show strong performance in structured domains such as mathematics and programming; however, they often lack pedagogical coherence and realistic teaching behaviors. To bridge this gap, we introduce Pedagogy-R1, a framework that adapts LRMs for classroom use through three innovations: (1) a distillation-based pipeline that filters and refines model outputs for instruction-tuning, (2) the Well-balanced Educational Benchmark (WBEB), which evaluates performance across subject knowledge, pedagogical knowledge, tracing, essay scoring, and teacher decision-making, and (3) a Chain-of-Pedagogy (CoP) prompting strategy for generating and eliciting teacher-style reasoning. Our mixed-method evaluation combines quantitative metrics with qualitative analysis, providing the first systematic assessment of LRMs' pedagogical strengths and limitations.

ScholarBench: A Bilingual Benchmark for Abstraction, Comprehension, and Reasoning Evaluation in Academic Contexts

Prior benchmarks for evaluating the domain-specific knowledge of large language models (LLMs) lack the scalability to handle complex academic tasks. To address this, we introduce \texttt{ScholarBench}, a benchmark centered on deep expert knowledge and complex academic problem-solving, which evaluates the academic reasoning ability of LLMs and is constructed through a three-step process. \texttt{ScholarBench} targets more specialized and logically complex contexts derived from academic literature, encompassing five distinct problem types. Unlike prior benchmarks, \texttt{ScholarBench} evaluates the abstraction, comprehension, and reasoning capabilities of LLMs across eight distinct research domains. To ensure high-quality evaluation data, we define category-specific example attributes and design questions that are aligned with the characteristic research methodologies and discourse structures of each domain. Additionally, this benchmark operates as an English-Korean bilingual dataset, facilitating simultaneous evaluation for linguistic capabilities of LLMs in both languages. The benchmark comprises 5,031 examples in Korean and 5,309 in English, with even state-of-the-art models like o3-mini achieving an average evaluation score of only 0.543, demonstrating the challenging nature of this benchmark.

Conformal mapping Coordinates Physics-Informed Neural Networks (CoCo-PINNs): learning neural networks for designing neutral inclusions

We focus on designing and solving the neutral inclusion problem via neural networks. The neutral inclusion problem has a long history in the theory of composite materials, and it is exceedingly challenging to identify the precise condition that precipitates a general-shaped inclusion into a neutral inclusion. Physics-informed neural networks (PINNs) have recently become a highly successful approach to addressing both forward and inverse problems associated with partial differential equations. We found that traditional PINNs perform inadequately when applied to the inverse problem of designing neutral inclusions with arbitrary shapes. In this study, we introduce a novel approach, Conformal mapping Coordinates Physics-Informed Neural Networks (CoCo-PINNs), which integrates complex analysis techniques into PINNs. This method exhibits strong performance in solving forward-inverse problems to construct neutral inclusions of arbitrary shapes in two dimensions, where the imperfect interface condition on the inclusion's boundary is modeled by training neural networks. Notably, we mathematically prove that training with a single linear field is sufficient to achieve neutrality for untrained linear fields in arbitrary directions, given a minor assumption. We demonstrate that CoCo-PINNs offer enhanced performances in terms of credibility, consistency, and stability.

Error analysis for finite element operator learning methods for solving parametric second-order elliptic PDEs

In this paper, we provide a theoretical analysis of a type of operator learning method without data reliance based on the classical finite element approximation, which is called the finite element operator network (FEONet). We first establish the convergence of this method for general second-order linear elliptic PDEs with respect to the parameters for neural network approximation. In this regard, we address the role of the condition number of the finite element matrix in the convergence of the method. Secondly, we derive an explicit error estimate for the self-adjoint case. For this, we investigate some regularity properties of the solution in certain function classes for a neural network approximation, verifying the sufficient condition for the solution to have the desired regularity. Finally, we will also conduct some numerical experiments that support the theoretical findings, confirming the role of the condition number of the finite element matrix in the overall convergence.

Asymptotic Properties for Bayesian Neural Network in Besov Space

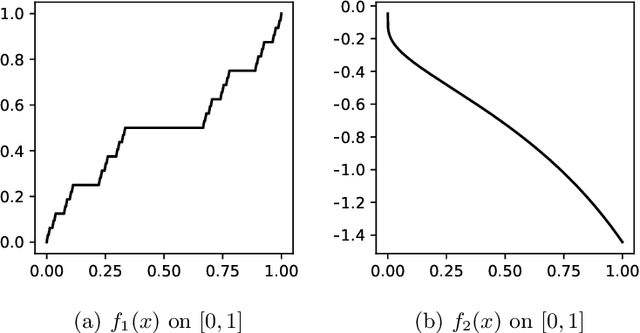
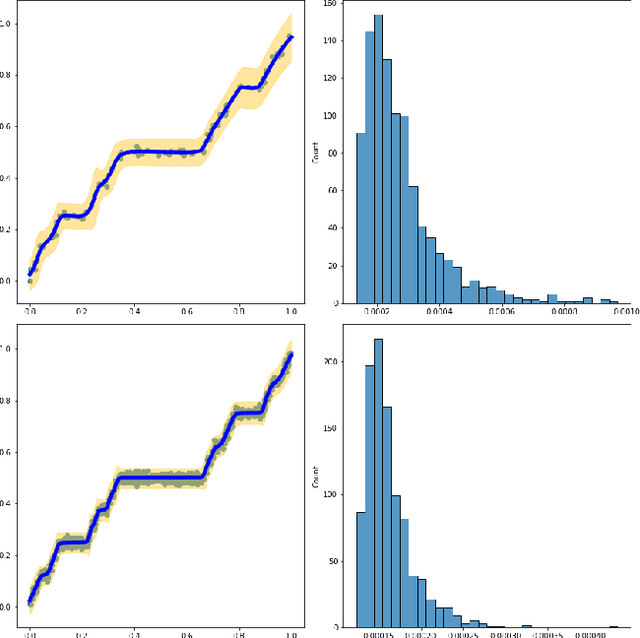
Neural networks have shown great predictive power when dealing with various unstructured data such as images and natural languages. The Bayesian neural network captures the uncertainty of prediction by putting a prior distribution for the parameter of the model and computing the posterior distribution. In this paper, we show that the Bayesian neural network using spike-and-slab prior has consistency with nearly minimax convergence rate when the true regression function is in the Besov space. Even when the smoothness of the regression function is unknown the same posterior convergence rate holds and thus the spike and slab prior is adaptive to the smoothness of the regression function. We also consider the shrinkage prior and show that it has the same convergence rate. In other words, we propose a practical Bayesian neural network with guaranteed asymptotic properties.

Generalized double Pareto shrinkage

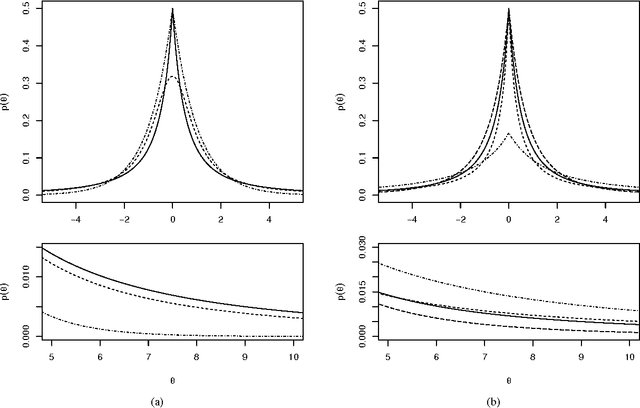
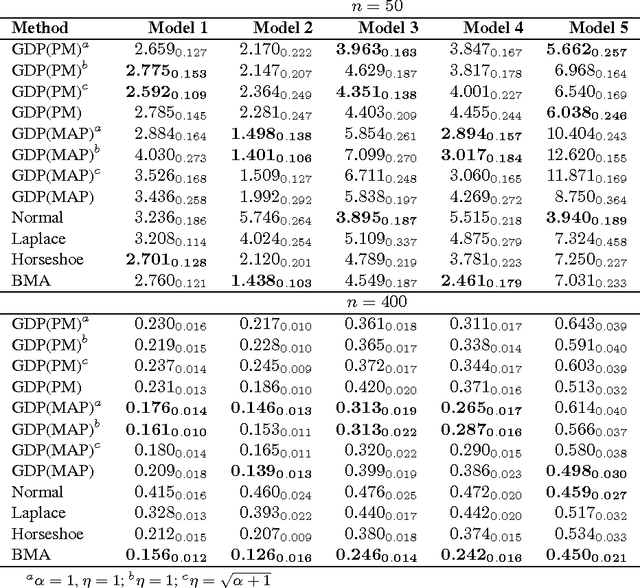
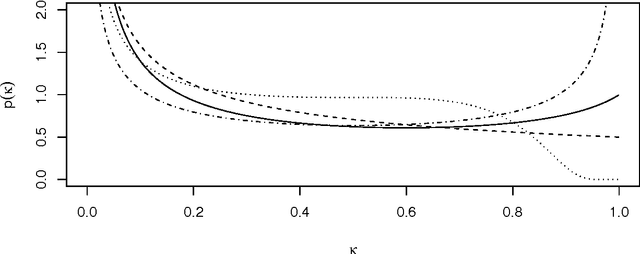
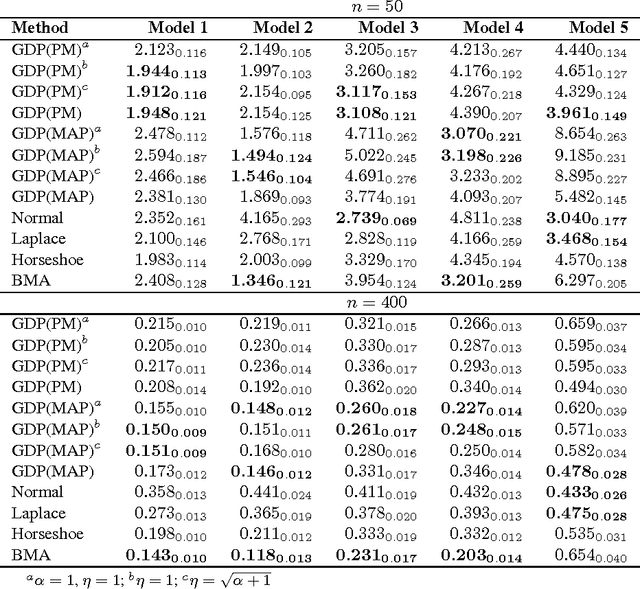
We propose a generalized double Pareto prior for Bayesian shrinkage estimation and inferences in linear models. The prior can be obtained via a scale mixture of Laplace or normal distributions, forming a bridge between the Laplace and Normal-Jeffreys' priors. While it has a spike at zero like the Laplace density, it also has a Student's $t$-like tail behavior. Bayesian computation is straightforward via a simple Gibbs sampling algorithm. We investigate the properties of the maximum a posteriori estimator, as sparse estimation plays an important role in many problems, reveal connections with some well-established regularization procedures, and show some asymptotic results. The performance of the prior is tested through simulations and an application.