Generalized double Pareto shrinkage
Paper and Code
Jan 26, 2013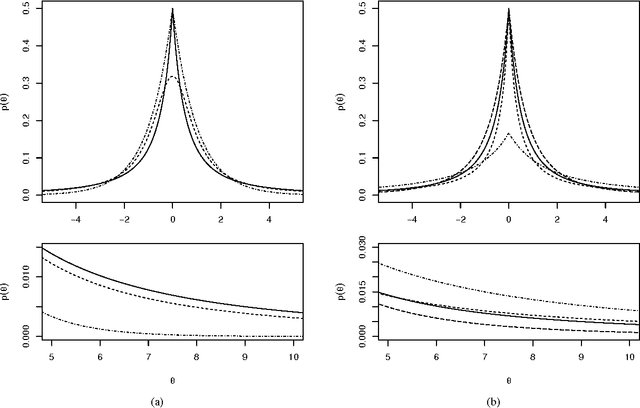
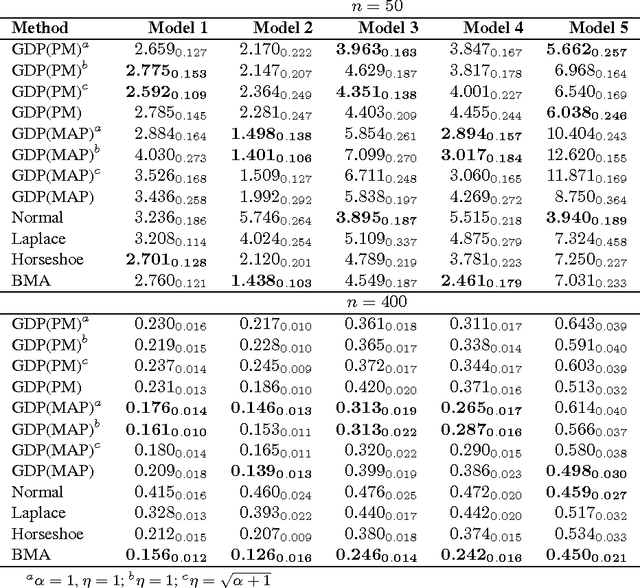
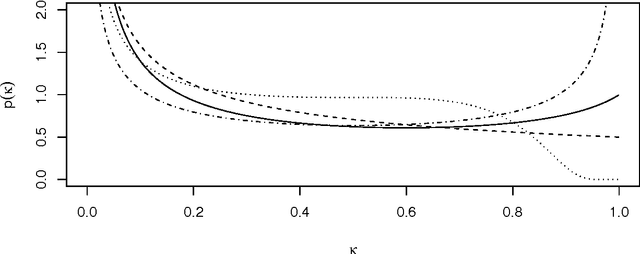
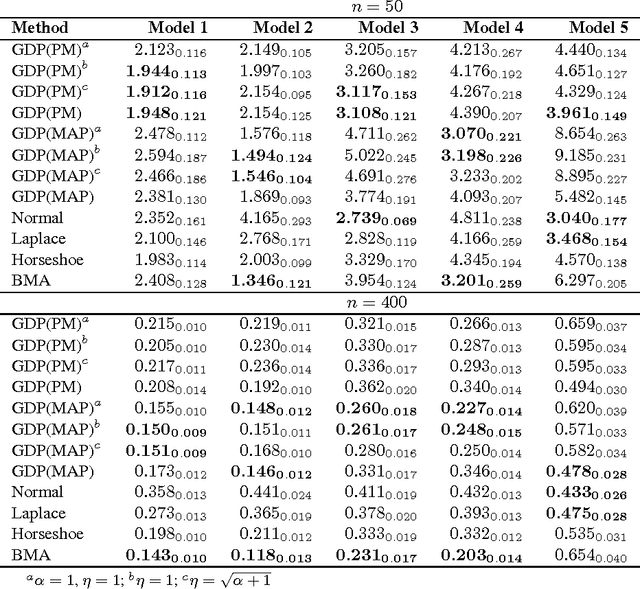
We propose a generalized double Pareto prior for Bayesian shrinkage estimation and inferences in linear models. The prior can be obtained via a scale mixture of Laplace or normal distributions, forming a bridge between the Laplace and Normal-Jeffreys' priors. While it has a spike at zero like the Laplace density, it also has a Student's $t$-like tail behavior. Bayesian computation is straightforward via a simple Gibbs sampling algorithm. We investigate the properties of the maximum a posteriori estimator, as sparse estimation plays an important role in many problems, reveal connections with some well-established regularization procedures, and show some asymptotic results. The performance of the prior is tested through simulations and an application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge