Physics-Informed Learning for Robust Acoustic Localization with Calibrated Uncertainty

Recent advances in Passive Acoustic Monitoring (PAM) offer an opportunity to obtain ecological spatial point-process data at unprecedented scale. However, realizing this opportunity necessitates the development of accurate and scalable localization methods. In real-world outdoor soundscapes, however, the assumptions underlying classical localization methods such as hyperbolic and score-based localization are routinely violated by multipath dominance, near-field effects, and complex propagation. Under these conditions, classical localization methods become brittle, with extreme errors possible even in small detection arrays. Rather than statistically replacing the underlying physics, we propose a method to refine it and increase robustness outside of ideal operating conditions: a learned model operating on physics-informed acoustic features corrects a fast hyperbolic solver where it produces implausible solutions, substantially reducing catastrophic worst-case errors while matching its median accuracy on field data. We further provide calibrated, geometry-aware uncertainty estimates suitable for propagation into downstream spatial models. Evaluating on distributed microphone arrays in real and simulated outdoor environments, we demonstrate that the proposed method yields robust, uncertainty-aware localization, providing a step toward scalable automated wildlife monitoring in complex acoustic environments.

ForestIR: Physics-Informed Forest Sound Simulation for Array-Based Bioacoustic Remote Sensing

Microphone array-based passive acoustic monitoring is increasingly used for biodiversity sensing in forests. However, design and evaluation of array systems and configurations remains difficult since field recordings are costly, difficult to reproduce, and provide limited control over forest and atmospheric conditions. We present ForestIR, a physics-informed and reproducible simulation framework that links forest and environmental conditions to microphone-array recordings for bioacoustic remote sensing. Through a more realistic sound propagation method and a systematic control over array design and environmental factors, ForestIR provides a practical simulation framework for optimizing array-based monitoring systems, especially for sound source localization purposes. ForestIR generates source-microphone impulse responses (IRs) under user-controlled forest and atmospheric conditions, and renders synthetic array recordings by convolving test signals with controlled background noise. We evaluate and demonstrate realistic features of ForestIR through experiments based on localization sensitivity to forest layout and atmospheric conditions, and also comparison between simulated IRs with sine-sweep IR measurements from a field experiment. ForestIR provides a practical way to test how forest and ground conditions, atmospheric state, and array geometry affect bioacoustic localization, and can support microphone-array design, robustness testing, and synthetic-data generation for passive acoustic monitoring.

Overfitted high-dimensional matrix factorizations via adaptive spectral shrinkage

Factor models are popular approaches for analyzing high-dimensional data to extract low-rank signals and estimate covariances. They decompose the covariance matrix as the sum of low-rank and diagonal components. A key issue is how to choose the latent dimension $k$, which is particularly challenging when the factor model only holds approximately and in low signal-to-noise scenarios. Bayesian overfitted factor models specify an upper bound on $k$ and rely on structured shrinkage priors to effectively remove extra components. Such approaches are popular and effective, but computationally expensive. We propose a much faster \texttt{EigenBayes} approach that provides valid uncertainty quantification, based on spectral estimation of latent factors and adaptive empirical Bayes calibration of key hyperparameters. The resulting posterior distribution factorizes across outcomes and is analytically tractable, bypassing Markov chain Monte Carlo. We show that \texttt{EigenBayes} adapts to the signal-to-noise ratio of each outcome and latent dimension, while shrinking superfluous latent components to zero. We establish favorable asymptotic properties and demonstrate strong empirical performance in numerical experiments and a genomics application, where EigenBayes outperforms state-of-the-art alternatives.

Learning Discrete Bayesian Networks with Hierarchical Dirichlet Shrinkage

Discrete Bayesian networks (DBNs) provide a broadly useful framework for modeling dependence structures in multivariate categorical data. There is a vast literature on methods for inferring conditional probabilities and graphical structure in DBNs, but data sparsity and parametric assumptions are major practical issues. In this article, we detail a comprehensive Bayesian framework for learning DBNs. First, we propose a hierarchical prior for the conditional probabilities that enables complicated interactions between parent variables and stability in sparse regimes. We give a novel Markov chain Monte Carlo (MCMC) algorithm utilizing parallel Langevin proposals to generate exact posterior samples, avoiding the pitfalls of variational approximations. Moreover, we verify that the full conditional distribution of the concentration parameters is log-concave under mild conditions, facilitating efficient sampling. We then propose two methods for learning network structures, including parent sets, Markov blankets, and DAGs, from categorical data. The first cycles through individual edges each MCMC iteration, whereas the second updates the entire structure as a single step. We evaluate the accuracy, power, and MCMC performance of our methods on several simulation studies. Finally, we apply our methodology to uncover prognostic network structure from primary breast cancer samples.

Spectral decomposition-assisted multi-study factor analysis

This article focuses on covariance estimation for multi-study data. Popular approaches employ factor-analytic terms with shared and study-specific loadings that decompose the variance into (i) a shared low-rank component, (ii) study-specific low-rank components, and (iii) a diagonal term capturing idiosyncratic variability. Our proposed methodology estimates the latent factors via spectral decompositions and infers the factor loadings via surrogate regression tasks, avoiding identifiability and computational issues of existing alternatives. Reliably inferring shared vs study-specific components requires novel developments that are of independent interest. The approximation error decreases as the sample size and the data dimension diverge, formalizing a blessing of dimensionality. Conditionally on the factors, loadings and residual error variances are inferred via conjugate normal-inverse gamma priors. The conditional posterior distribution of factor loadings has a simple product form across outcomes, facilitating parallelization. We show favorable asymptotic properties, including central limit theorems for point estimators and posterior contraction, and excellent empirical performance in simulations. The methods are applied to integrate three studies on gene associations among immune cells.

On the Statistical Capacity of Deep Generative Models

Deep generative models are routinely used in generating samples from complex, high-dimensional distributions. Despite their apparent successes, their statistical properties are not well understood. A common assumption is that with enough training data and sufficiently large neural networks, deep generative model samples will have arbitrarily small errors in sampling from any continuous target distribution. We set up a unifying framework that debunks this belief. We demonstrate that broad classes of deep generative models, including variational autoencoders and generative adversarial networks, are not universal generators. Under the predominant case of Gaussian latent variables, these models can only generate concentrated samples that exhibit light tails. Using tools from concentration of measure and convex geometry, we give analogous results for more general log-concave and strongly log-concave latent variable distributions. We extend our results to diffusion models via a reduction argument. We use the Gromov--Levy inequality to give similar guarantees when the latent variables lie on manifolds with positive Ricci curvature. These results shed light on the limited capacity of common deep generative models to handle heavy tails. We illustrate the empirical relevance of our work with simulations and financial data.

Fast nonparametric feature selection with error control using integrated path stability selection

Feature selection can greatly improve performance and interpretability in machine learning problems. However, existing nonparametric feature selection methods either lack theoretical error control or fail to accurately control errors in practice. Many methods are also slow, especially in high dimensions. In this paper, we introduce a general feature selection method that applies integrated path stability selection to thresholding to control false positives and the false discovery rate. The method also estimates q-values, which are better suited to high-dimensional data than p-values. We focus on two special cases of the general method based on gradient boosting (IPSSGB) and random forests (IPSSRF). Extensive simulations with RNA sequencing data show that IPSSGB and IPSSRF have better error control, detect more true positives, and are faster than existing methods. We also use both methods to detect microRNAs and genes related to ovarian cancer, finding that they make better predictions with fewer features than other methods.

Bayesian Joint Additive Factor Models for Multiview Learning

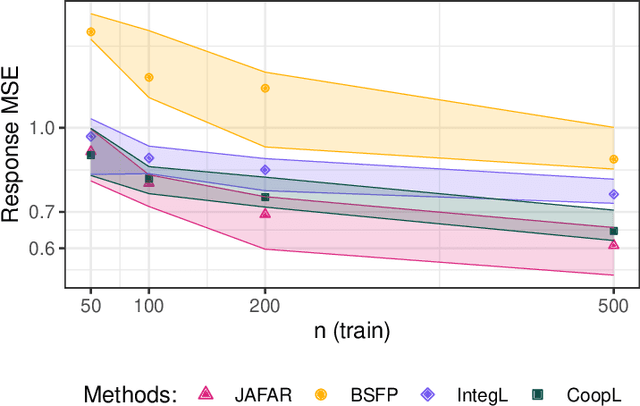
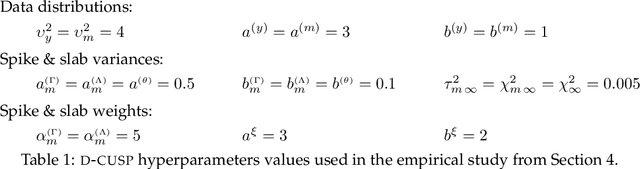
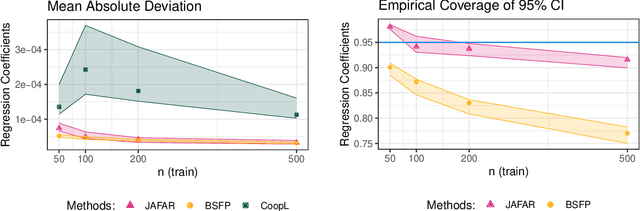
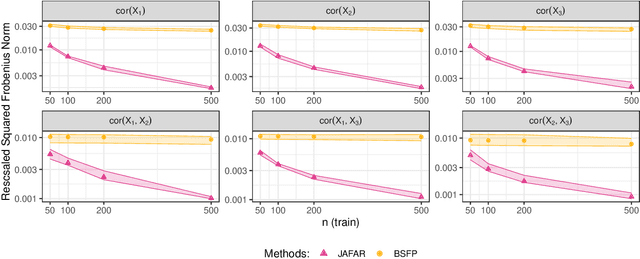
It is increasingly common in a wide variety of applied settings to collect data of multiple different types on the same set of samples. Our particular focus in this article is on studying relationships between such multiview features and responses. A motivating application arises in the context of precision medicine where multi-omics data are collected to correlate with clinical outcomes. It is of interest to infer dependence within and across views while combining multimodal information to improve the prediction of outcomes. The signal-to-noise ratio can vary substantially across views, motivating more nuanced statistical tools beyond standard late and early fusion. This challenge comes with the need to preserve interpretability, select features, and obtain accurate uncertainty quantification. We propose a joint additive factor regression model (JAFAR) with a structured additive design, accounting for shared and view-specific components. We ensure identifiability via a novel dependent cumulative shrinkage process (D-CUSP) prior. We provide an efficient implementation via a partially collapsed Gibbs sampler and extend our approach to allow flexible feature and outcome distributions. Prediction of time-to-labor onset from immunome, metabolome, and proteome data illustrates performance gains against state-of-the-art competitors. Our open-source software (R package) is available at https://github.com/niccoloanceschi/jafar.

Logistic-beta processes for modeling dependent random probabilities with beta marginals

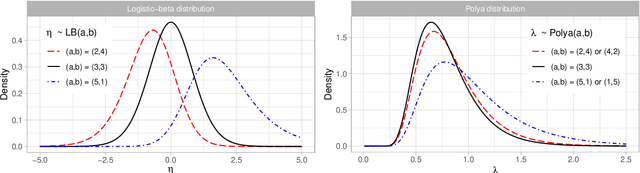
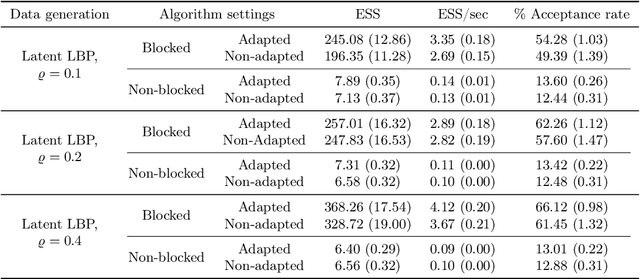
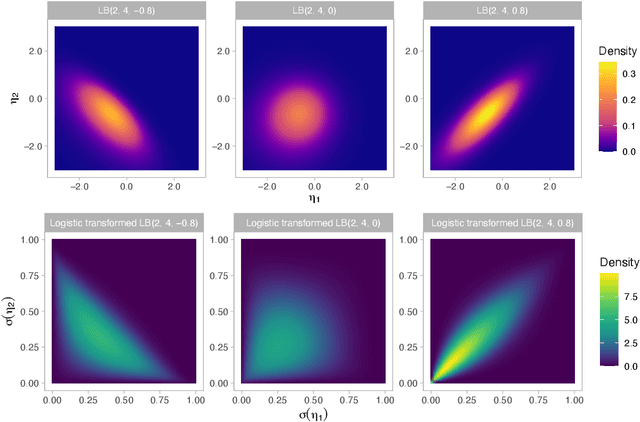
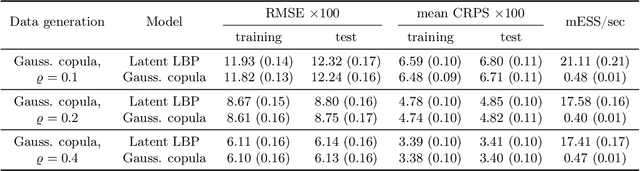
The beta distribution serves as a canonical tool for modeling probabilities and is extensively used in statistics and machine learning, especially in the field of Bayesian nonparametrics. Despite its widespread use, there is limited work on flexible and computationally convenient stochastic process extensions for modeling dependent random probabilities. We propose a novel stochastic process called the logistic-beta process, whose logistic transformation yields a stochastic process with common beta marginals. Similar to the Gaussian process, the logistic-beta process can model dependence on both discrete and continuous domains, such as space or time, and has a highly flexible dependence structure through correlation kernels. Moreover, its normal variance-mean mixture representation leads to highly effective posterior inference algorithms. The flexibility and computational benefits of logistic-beta processes are demonstrated through nonparametric binary regression simulation studies. Furthermore, we apply the logistic-beta process in modeling dependent Dirichlet processes, and illustrate its application and benefits through Bayesian density regression problems in a toxicology study.

Bayesian Transfer Learning

Transfer learning is a burgeoning concept in statistical machine learning that seeks to improve inference and/or predictive accuracy on a domain of interest by leveraging data from related domains. While the term "transfer learning" has garnered much recent interest, its foundational principles have existed for years under various guises. Prior literature reviews in computer science and electrical engineering have sought to bring these ideas into focus, primarily surveying general methodologies and works from these disciplines. This article highlights Bayesian approaches to transfer learning, which have received relatively limited attention despite their innate compatibility with the notion of drawing upon prior knowledge to guide new learning tasks. Our survey encompasses a wide range of Bayesian transfer learning frameworks applicable to a variety of practical settings. We discuss how these methods address the problem of finding the optimal information to transfer between domains, which is a central question in transfer learning. We illustrate the utility of Bayesian transfer learning methods via a simulation study where we compare performance against frequentist competitors.