On the Statistical Capacity of Deep Generative Models

Deep generative models are routinely used in generating samples from complex, high-dimensional distributions. Despite their apparent successes, their statistical properties are not well understood. A common assumption is that with enough training data and sufficiently large neural networks, deep generative model samples will have arbitrarily small errors in sampling from any continuous target distribution. We set up a unifying framework that debunks this belief. We demonstrate that broad classes of deep generative models, including variational autoencoders and generative adversarial networks, are not universal generators. Under the predominant case of Gaussian latent variables, these models can only generate concentrated samples that exhibit light tails. Using tools from concentration of measure and convex geometry, we give analogous results for more general log-concave and strongly log-concave latent variable distributions. We extend our results to diffusion models via a reduction argument. We use the Gromov--Levy inequality to give similar guarantees when the latent variables lie on manifolds with positive Ricci curvature. These results shed light on the limited capacity of common deep generative models to handle heavy tails. We illustrate the empirical relevance of our work with simulations and financial data.

A Distributional Evaluation of Generative Image Models

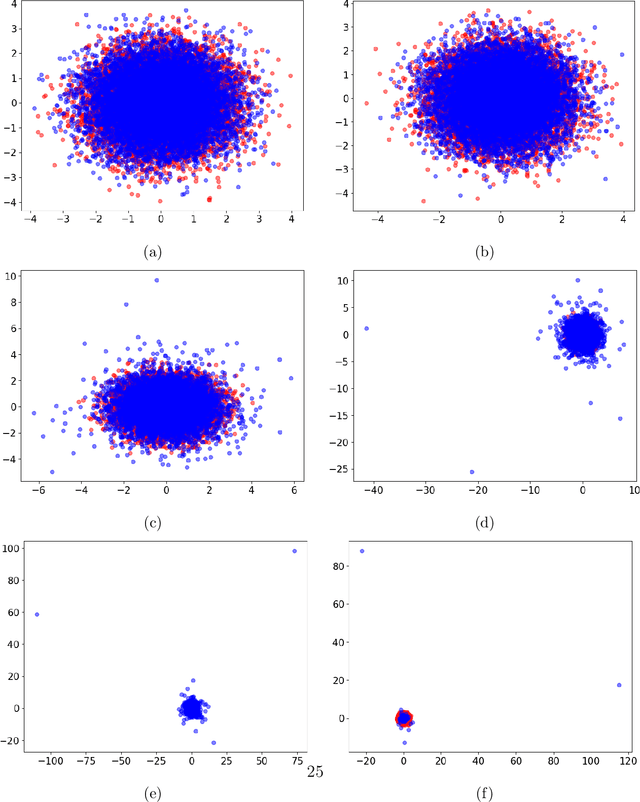
Generative models are ubiquitous in modern artificial intelligence (AI) applications. Recent advances have led to a variety of generative modeling approaches that are capable of synthesizing highly realistic samples. Despite these developments, evaluating the distributional match between the synthetic samples and the target distribution in a statistically principled way remains a core challenge. We focus on evaluating image generative models, where studies often treat human evaluation as the gold standard. Commonly adopted metrics, such as the Fr\'echet Inception Distance (FID), do not sufficiently capture the differences between the learned and target distributions, because the assumption of normality ignores differences in the tails. We propose the Embedded Characteristic Score (ECS), a comprehensive metric for evaluating the distributional match between the learned and target sample distributions, and explore its connection with moments and tail behavior. We derive natural properties of ECS and show its practical use via simulations and an empirical study.

Spectral Gap Regularization of Neural Networks

We introduce Fiedler regularization, a novel approach for regularizing neural networks that utilizes spectral/graphical information. Existing regularization methods often focus on penalizing weights in a global/uniform manner that ignores the connectivity structure of the neural network. We propose to use the Fiedler value of the neural network's underlying graph as a tool for regularization. We provide theoretical motivation for this approach via spectral graph theory. We demonstrate several useful properties of the Fiedler value that make it useful as a regularization tool. We provide an approximate, variational approach for faster computation during training. We provide an alternative formulation of this framework in the form of a structurally weighted $\text{L}_1$ penalty, thus linking our approach to sparsity induction. We provide uniform generalization error bounds for Fiedler regularization via a Rademacher complexity analysis. We performed experiments on datasets that compare Fiedler regularization with classical regularization methods such as dropout and weight decay. Results demonstrate the efficacy of Fiedler regularization. This is a journal extension of the conference paper by Tam and Dunson (2020).

Multiscale Graph Comparison via the Embedded Laplacian Distance

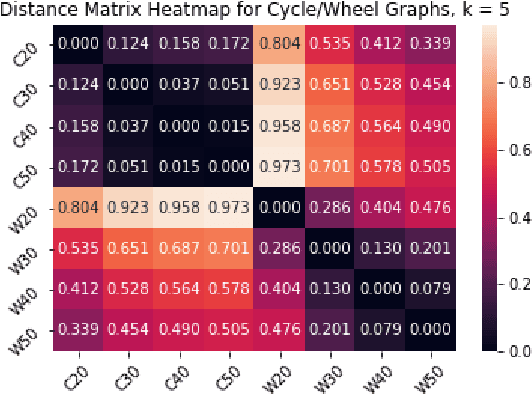
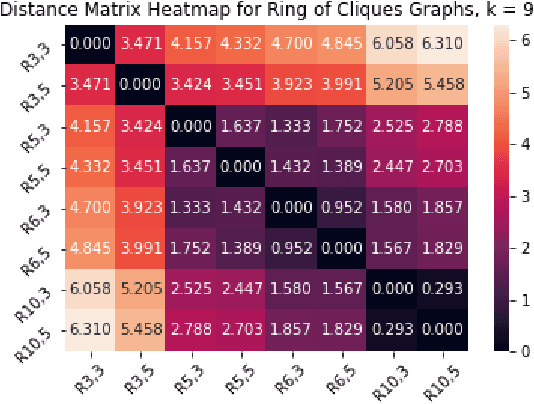
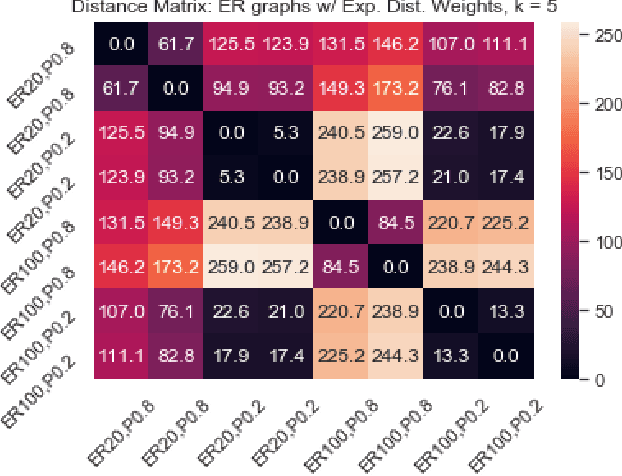
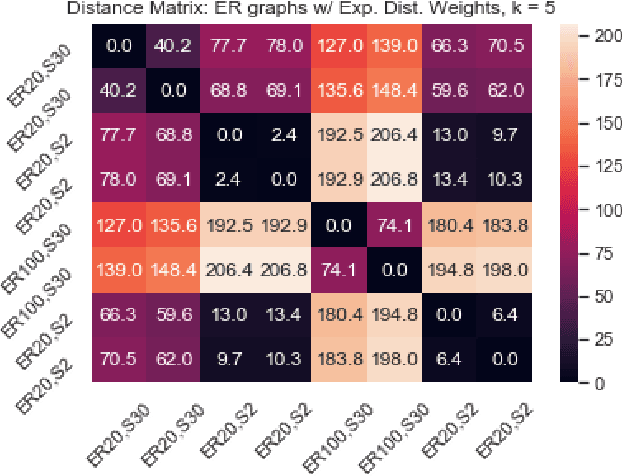
We introduce a simple and fast method for comparing graphs of different sizes. Existing approaches are often either limited to comparing graphs with the same number of vertices or are computationally unscalable. We propose the Embedded Laplacian Distance (ELD) for comparing graphs of potentially vastly different sizes. Our approach first projects the graphs onto a common, low-dimensional Laplacian embedding space that respects graphical structure. This reduces the problem to that of comparing point clouds in a Euclidean space. A distance can then be computed efficiently via a natural sliced Wasserstein approach. We show that the ELD is a pseudo-metric and is invariant under graph isomorphism. We provide intuitive interpretations of the ELD using tools from spectral graph theory. We test the efficacy of the ELD approach extensively on both simulated and real data. Results obtained are excellent.

Fiedler Regularization: Learning Neural Networks with Graph Sparsity

We introduce a novel regularization approach for deep learning that incorporates and respects the underlying graphical structure of the neural network. Existing regularization methods often focus on dropping/penalizing weights in a global manner that ignores the connectivity structure of the neural network. We propose to use the Fiedler value of the neural network's underlying graph as a tool for regularization. We provide theoretical support for this approach via spectral graph theory. We demonstrate the convexity of this penalty and provide an approximate, variational approach for fast computation in practical training of neural networks. We provide bounds on such approximations. We provide an alternative but equivalent formulation of this framework in the form of a structurally weighted L1 penalty, thus linking our approach to sparsity induction. We performed experiments on datasets that compare Fiedler regularization with traditional regularization methods such as dropout and weight decay. Results demonstrate the efficacy of Fiedler regularization.