Barbara E Engelhardt
Preference-Guided Diffusion for Multi-Objective Offline Optimization
Mar 21, 2025
Abstract:Offline multi-objective optimization aims to identify Pareto-optimal solutions given a dataset of designs and their objective values. In this work, we propose a preference-guided diffusion model that generates Pareto-optimal designs by leveraging a classifier-based guidance mechanism. Our guidance classifier is a preference model trained to predict the probability that one design dominates another, directing the diffusion model toward optimal regions of the design space. Crucially, this preference model generalizes beyond the training distribution, enabling the discovery of Pareto-optimal solutions outside the observed dataset. We introduce a novel diversity-aware preference guidance, augmenting Pareto dominance preference with diversity criteria. This ensures that generated solutions are optimal and well-distributed across the objective space, a capability absent in prior generative methods for offline multi-objective optimization. We evaluate our approach on various continuous offline multi-objective optimization tasks and find that it consistently outperforms other inverse/generative approaches while remaining competitive with forward/surrogate-based optimization methods. Our results highlight the effectiveness of classifier-guided diffusion models in generating diverse and high-quality solutions that approximate the Pareto front well.
A Distributional Evaluation of Generative Image Models
Jan 01, 2025
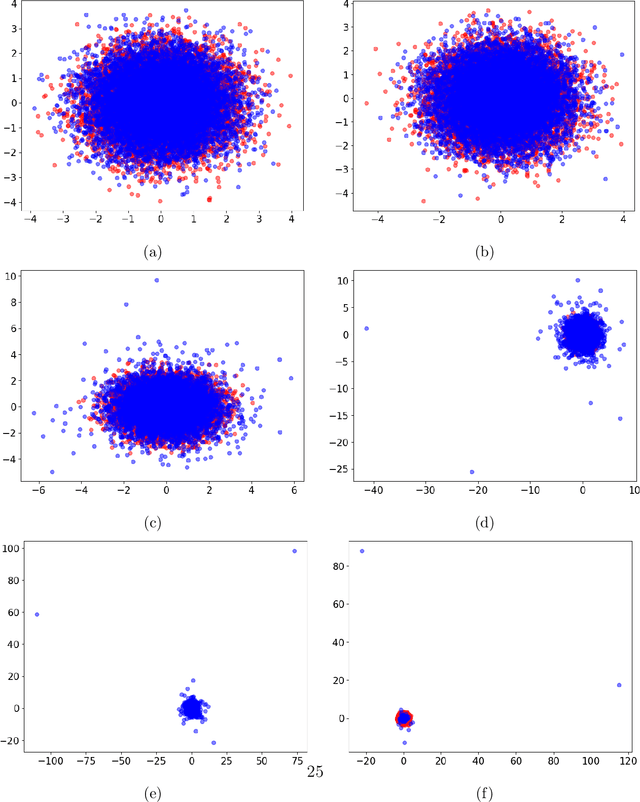
Abstract:Generative models are ubiquitous in modern artificial intelligence (AI) applications. Recent advances have led to a variety of generative modeling approaches that are capable of synthesizing highly realistic samples. Despite these developments, evaluating the distributional match between the synthetic samples and the target distribution in a statistically principled way remains a core challenge. We focus on evaluating image generative models, where studies often treat human evaluation as the gold standard. Commonly adopted metrics, such as the Fr\'echet Inception Distance (FID), do not sufficiently capture the differences between the learned and target distributions, because the assumption of normality ignores differences in the tails. We propose the Embedded Characteristic Score (ECS), a comprehensive metric for evaluating the distributional match between the learned and target sample distributions, and explore its connection with moments and tail behavior. We derive natural properties of ECS and show its practical use via simulations and an empirical study.
Defining Admissible Rewards for High Confidence Policy Evaluation
May 30, 2019

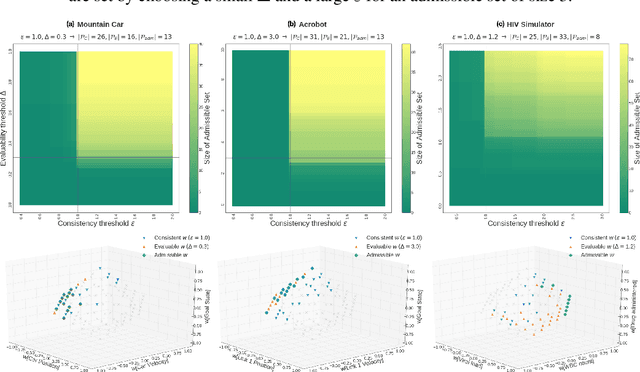

Abstract:A key impediment to reinforcement learning (RL) in real applications with limited, batch data is defining a reward function that reflects what we implicitly know about reasonable behaviour for a task and allows for robust off-policy evaluation. In this work, we develop a method to identify an admissible set of reward functions for policies that (a) do not diverge too far from past behaviour, and (b) can be evaluated with high confidence, given only a collection of past trajectories. Together, these ensure that we propose policies that we trust to be implemented in high-risk settings. We demonstrate our approach to reward design on synthetic domains as well as in a critical care context, for a reward that consolidates clinical objectives to learn a policy for weaning patients from mechanical ventilation.
An Optimal Policy for Patient Laboratory Tests in Intensive Care Units
Aug 14, 2018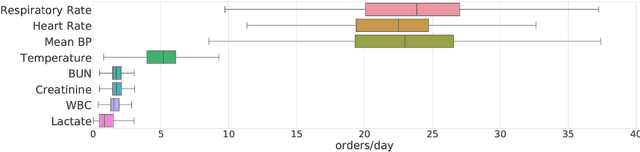
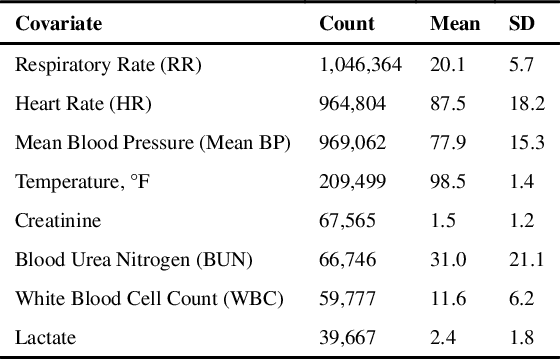
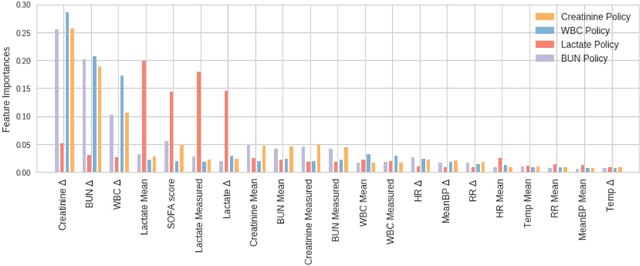
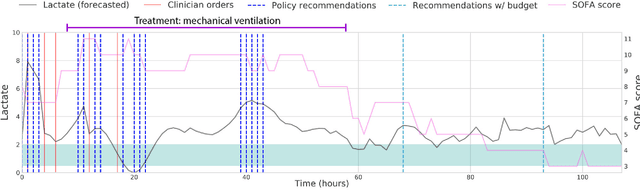
Abstract:Laboratory testing is an integral tool in the management of patient care in hospitals, particularly in intensive care units (ICUs). There exists an inherent trade-off in the selection and timing of lab tests between considerations of the expected utility in clinical decision-making of a given test at a specific time, and the associated cost or risk it poses to the patient. In this work, we introduce a framework that learns policies for ordering lab tests which optimizes for this trade-off. Our approach uses batch off-policy reinforcement learning with a composite reward function based on clinical imperatives, applied to data that include examples of clinicians ordering labs for patients. To this end, we develop and extend principles of Pareto optimality to improve the selection of actions based on multiple reward function components while respecting typical procedural considerations and prioritization of clinical goals in the ICU. Our experiments show that we can estimate a policy that reduces the frequency of lab tests and optimizes timing to minimize information redundancy. We also find that the estimated policies typically suggest ordering lab tests well ahead of critical onsets--such as mechanical ventilation or dialysis--that depend on the lab results. We evaluate our approach by quantifying how these policies may initiate earlier onset of treatment.
Sparse Multi-Output Gaussian Processes for Medical Time Series Prediction
Jun 21, 2018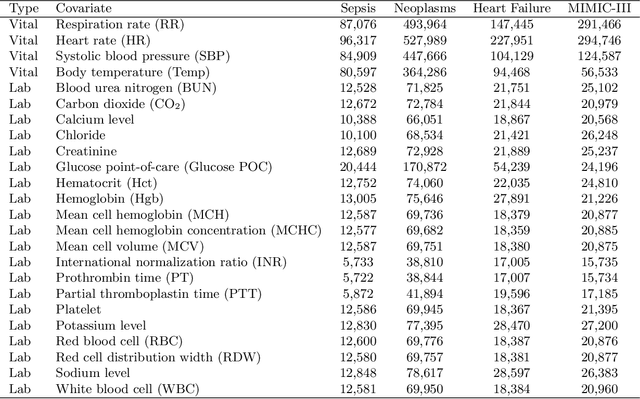
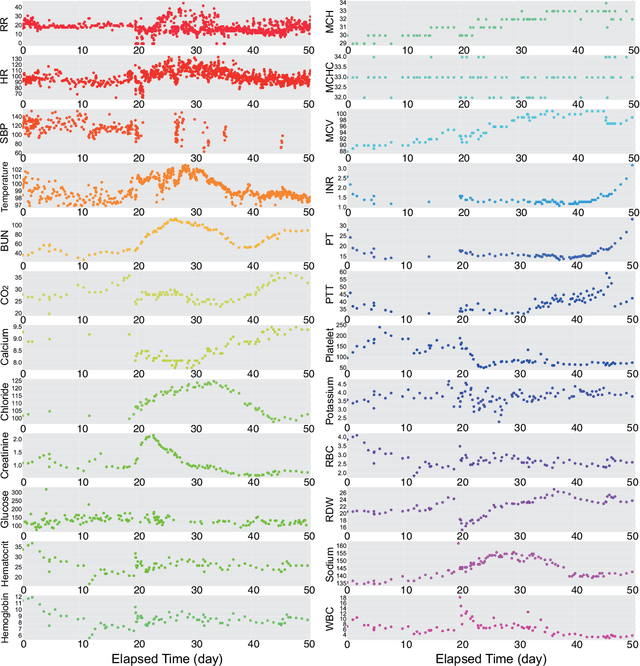
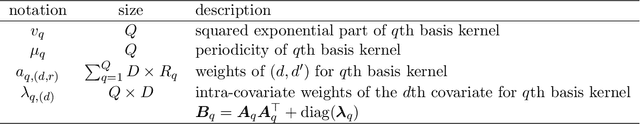
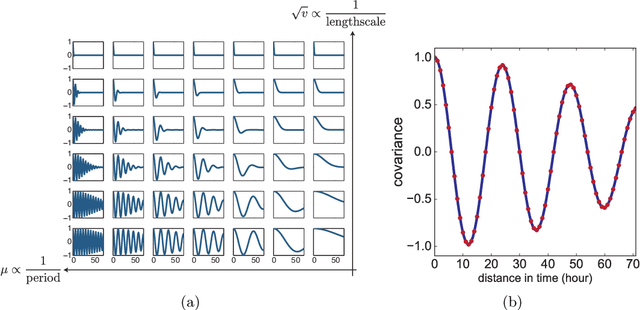
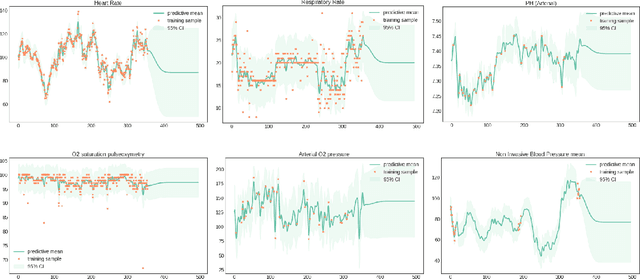
Abstract:In the scenario of real-time monitoring of hospital patients, high-quality inference of patients' health status using all information available from clinical covariates and lab tests is essential to enable successful medical interventions and improve patient outcomes. Developing a computational framework that can learn from observational large-scale electronic health records (EHRs) and make accurate real-time predictions is a critical step. In this work, we develop and explore a Bayesian nonparametric model based on Gaussian process (GP) regression for hospital patient monitoring. We propose MedGP, a statistical framework that incorporates 24 clinical and lab covariates and supports a rich reference data set from which relationships between observed covariates may be inferred and exploited for high-quality inference of patient state over time. To do this, we develop a highly structured sparse GP kernel to enable tractable computation over tens of thousands of time points while estimating correlations among clinical covariates, patients, and periodicity in patient observations. MedGP has a number of benefits over current methods, including (i) not requiring an alignment of the time series data, (ii) quantifying confidence regions in the predictions, (iii) exploiting a vast and rich database of patients, and (iv) inferring interpretable relationships among clinical covariates. We evaluate and compare results from MedGP on the task of online prediction for three patient subgroups from two medical data sets across 8,043 patients. We found MedGP improves online prediction over baseline methods for nearly all covariates across different disease subgroups and studies. The publicly available code is at https://github.com/bee-hive/MedGP.
PG-TS: Improved Thompson Sampling for Logistic Contextual Bandits
May 18, 2018


Abstract:We address the problem of regret minimization in logistic contextual bandits, where a learner decides among sequential actions or arms given their respective contexts to maximize binary rewards. Using a fast inference procedure with Polya-Gamma distributed augmentation variables, we propose an improved version of Thompson Sampling, a Bayesian formulation of contextual bandits with near-optimal performance. Our approach, Polya-Gamma augmented Thompson Sampling (PG-TS), achieves state-of-the-art performance on simulated and real data. PG-TS explores the action space efficiently and exploits high-reward arms, quickly converging to solutions of low regret. Its explicit estimation of the posterior distribution of the context feature covariance leads to substantial empirical gains over approximate approaches. PG-TS is the first approach to demonstrate the benefits of Polya-Gamma augmentation in bandits and to propose an efficient Gibbs sampler for approximating the analytically unsolvable integral of logistic contextual bandits.
Large Linear Multi-output Gaussian Process Learning
Oct 23, 2017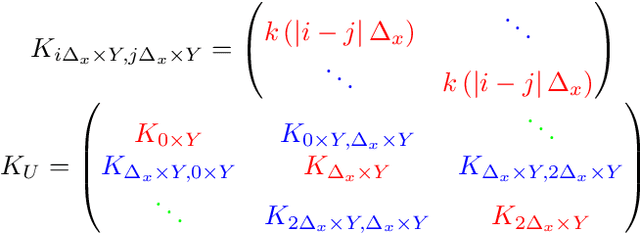

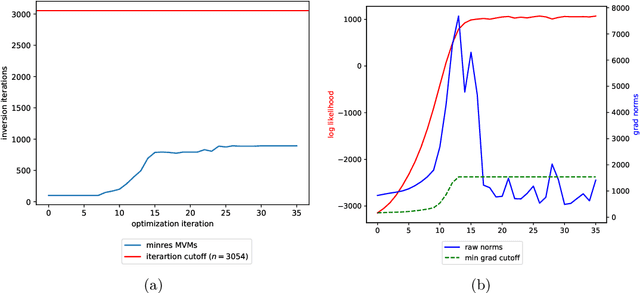
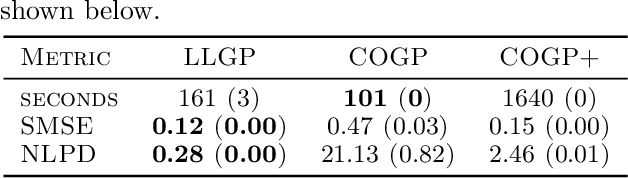
Abstract:Gaussian processes (GPs), or distributions over arbitrary functions in a continuous domain, can be generalized to the multi-output case: a linear model of coregionalization (LMC) is one approach. LMCs estimate and exploit correlations across the multiple outputs. While model estimation can be performed efficiently for single-output GPs, these assume stationarity, but in the multi-output case the cross-covariance interaction is not stationary. We propose Large Linear GP (LLGP), which circumvents the need for stationarity by inducing structure in the LMC kernel through a common grid of inputs shared between outputs, enabling optimization of GP hyperparameters for multi-dimensional outputs and low-dimensional inputs. When applied to synthetic two-dimensional and real time series data, we find our theoretical improvement relative to the current solutions for multi-output GPs is realized with LLGP reducing training time while improving or maintaining predictive mean accuracy. Moreover, by using a direct likelihood approximation rather than a variational one, model confidence estimates are significantly improved.
A Reinforcement Learning Approach to Weaning of Mechanical Ventilation in Intensive Care Units
Apr 20, 2017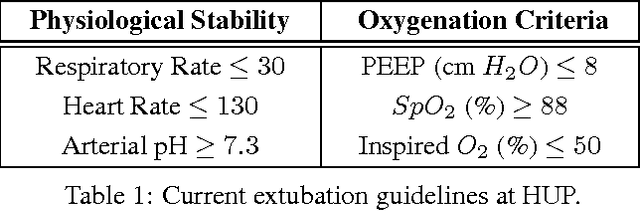
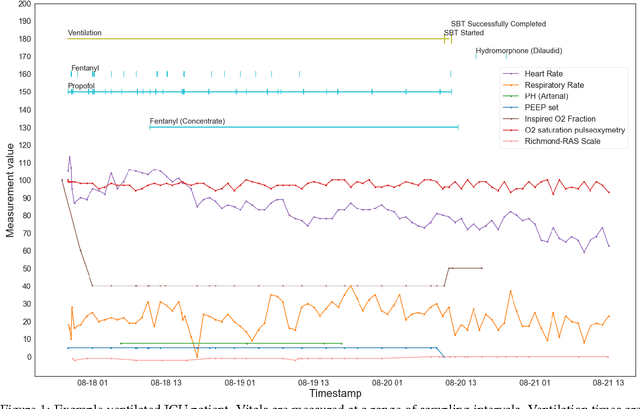
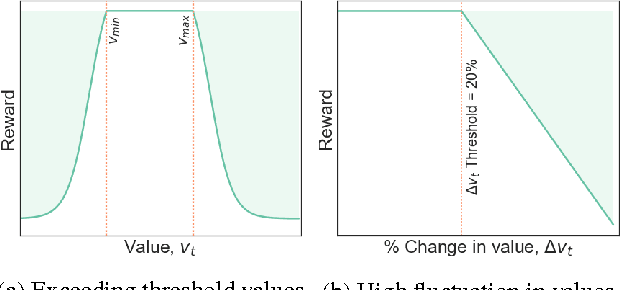
Abstract:The management of invasive mechanical ventilation, and the regulation of sedation and analgesia during ventilation, constitutes a major part of the care of patients admitted to intensive care units. Both prolonged dependence on mechanical ventilation and premature extubation are associated with increased risk of complications and higher hospital costs, but clinical opinion on the best protocol for weaning patients off of a ventilator varies. This work aims to develop a decision support tool that uses available patient information to predict time-to-extubation readiness and to recommend a personalized regime of sedation dosage and ventilator support. To this end, we use off-policy reinforcement learning algorithms to determine the best action at a given patient state from sub-optimal historical ICU data. We compare treatment policies from fitted Q-iteration with extremely randomized trees and with feedforward neural networks, and demonstrate that the policies learnt show promise in recommending weaning protocols with improved outcomes, in terms of minimizing rates of reintubation and regulating physiological stability.
Nonparametric Reduced-Rank Regression for Multi-SNP, Multi-Trait Association Mapping
Dec 08, 2015



Abstract:Genome-wide association studies have proven to be essential for understanding the genetic basis of disease. However, many complex traits---personality traits, facial features, disease subtyping---are inherently high-dimensional, impeding simple approaches to association mapping. We developed a nonparametric Bayesian reduced rank regression model for multi-SNP, multi-trait association mapping that does not require the rank of the linear subspace to be specified. We show in simulations and real data that our model shares strength over SNPs and over correlated traits, improving statistical power to identify genetic associations with an interpretable, SNP-supervised low-dimensional linear projection of the high-dimensional phenotype. On the HapMap phase 3 gene expression QTL study data, we identify pleiotropic expression QTLs that classical univariate tests are underpowered to find and that two step approaches cannot recover. Our Python software, BERRRI, is publicly available at GitHub: https://github.com/ashlee1031/BERRRI.
Bayesian group latent factor analysis with structured sparsity
Nov 11, 2015

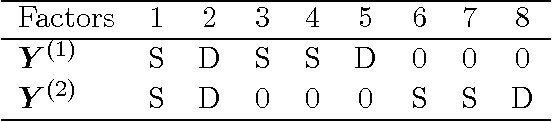

Abstract:Latent factor models are the canonical statistical tool for exploratory analyses of low-dimensional linear structure for an observation matrix with p features across n samples. We develop a structured Bayesian group factor analysis model that extends the factor model to multiple coupled observation matrices; in the case of two observations, this reduces to a Bayesian model of canonical correlation analysis. The main contribution of this work is to carefully define a structured Bayesian prior that encourages both element-wise and column-wise shrinkage and leads to desirable behavior on high-dimensional data. In particular, our model puts a structured prior on the joint factor loading matrix, regularizing at three levels, which enables element-wise sparsity and unsupervised recovery of latent factors corresponding to structured variance across arbitrary subsets of the observations. In addition, our structured prior allows for both dense and sparse latent factors so that covariation among either all features or only a subset of features can both be recovered. We use fast parameter-expanded expectation-maximization for parameter estimation in this model. We validate our method on both simulated data with substantial structure and real data, comparing against a number of state-of-the-art approaches. These results illustrate useful properties of our model, including i) recovering sparse signal in the presence of dense effects; ii) the ability to scale naturally to large numbers of observations; iii) flexible observation- and factor-specific regularization to recover factors with a wide variety of sparsity levels and percentage of variance explained; and iv) tractable inference that scales to modern genomic and document data sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge