Large Linear Multi-output Gaussian Process Learning
Paper and Code
Oct 23, 2017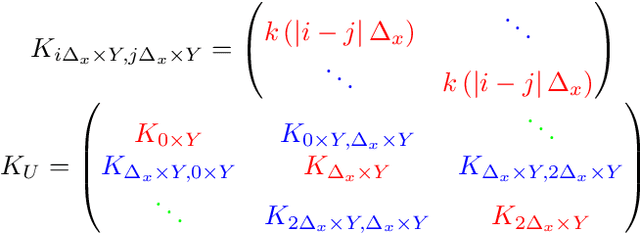

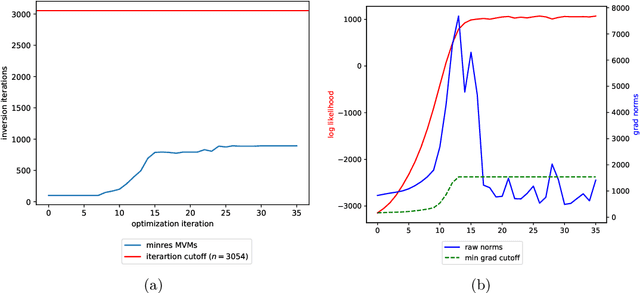
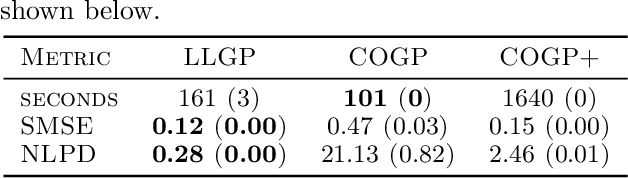
Gaussian processes (GPs), or distributions over arbitrary functions in a continuous domain, can be generalized to the multi-output case: a linear model of coregionalization (LMC) is one approach. LMCs estimate and exploit correlations across the multiple outputs. While model estimation can be performed efficiently for single-output GPs, these assume stationarity, but in the multi-output case the cross-covariance interaction is not stationary. We propose Large Linear GP (LLGP), which circumvents the need for stationarity by inducing structure in the LMC kernel through a common grid of inputs shared between outputs, enabling optimization of GP hyperparameters for multi-dimensional outputs and low-dimensional inputs. When applied to synthetic two-dimensional and real time series data, we find our theoretical improvement relative to the current solutions for multi-output GPs is realized with LLGP reducing training time while improving or maintaining predictive mean accuracy. Moreover, by using a direct likelihood approximation rather than a variational one, model confidence estimates are significantly improved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge