Syrine Belakaria
Sharpe Ratio-Guided Active Learning for Preference Optimization in RLHF
Mar 28, 2025Abstract:Reinforcement learning from human feedback (RLHF) has become a cornerstone of the training and alignment pipeline for large language models (LLMs). Recent advances, such as direct preference optimization (DPO), have simplified the preference learning step. However, collecting preference data remains a challenging and costly process, often requiring expert annotation. This cost can be mitigated by carefully selecting the data points presented for annotation. In this work, we propose an active learning approach to efficiently select prompt and preference pairs using a risk assessment strategy based on the Sharpe Ratio. To address the challenge of unknown preferences prior to annotation, our method evaluates the gradients of all potential preference annotations to assess their impact on model updates. These gradient-based evaluations enable risk assessment of data points regardless of the annotation outcome. By leveraging the DPO loss derivations, we derive a closed-form expression for computing these Sharpe ratios on a per-tuple basis, ensuring our approach remains both tractable and computationally efficient. We also introduce two variants of our method, each making different assumptions about prior information. Experimental results demonstrate that our method outperforms the baseline by up to 5% in win rates against the chosen completion with limited human preference data across several language models and real-world datasets.
Preference-Guided Diffusion for Multi-Objective Offline Optimization
Mar 21, 2025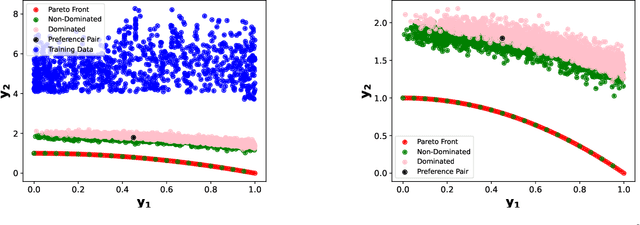
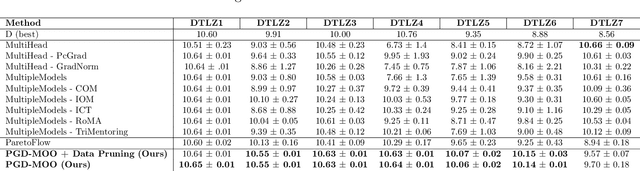
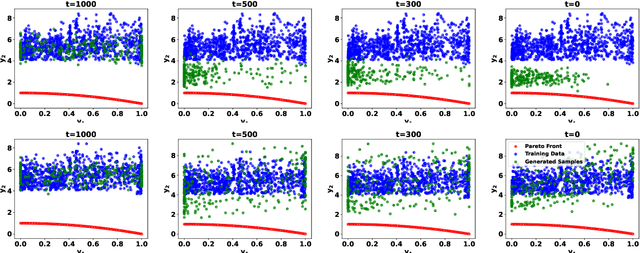
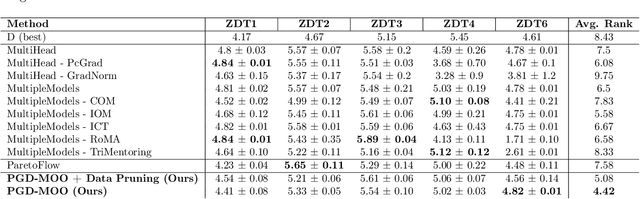
Abstract:Offline multi-objective optimization aims to identify Pareto-optimal solutions given a dataset of designs and their objective values. In this work, we propose a preference-guided diffusion model that generates Pareto-optimal designs by leveraging a classifier-based guidance mechanism. Our guidance classifier is a preference model trained to predict the probability that one design dominates another, directing the diffusion model toward optimal regions of the design space. Crucially, this preference model generalizes beyond the training distribution, enabling the discovery of Pareto-optimal solutions outside the observed dataset. We introduce a novel diversity-aware preference guidance, augmenting Pareto dominance preference with diversity criteria. This ensures that generated solutions are optimal and well-distributed across the objective space, a capability absent in prior generative methods for offline multi-objective optimization. We evaluate our approach on various continuous offline multi-objective optimization tasks and find that it consistently outperforms other inverse/generative approaches while remaining competitive with forward/surrogate-based optimization methods. Our results highlight the effectiveness of classifier-guided diffusion models in generating diverse and high-quality solutions that approximate the Pareto front well.
Non-Myopic Multi-Objective Bayesian Optimization
Dec 11, 2024Abstract:We consider the problem of finite-horizon sequential experimental design to solve multi-objective optimization (MOO) of expensive black-box objective functions. This problem arises in many real-world applications, including materials design, where we have a small resource budget to make and evaluate candidate materials in the lab. We solve this problem using the framework of Bayesian optimization (BO) and propose the first set of non-myopic methods for MOO problems. Prior work on non-myopic BO for single-objective problems relies on the Bellman optimality principle to handle the lookahead reasoning process. However, this principle does not hold for most MOO problems because the reward function needs to satisfy some conditions: scalar variable, monotonicity, and additivity. We address this challenge by using hypervolume improvement (HVI) as our scalarization approach, which allows us to use a lower-bound on the Bellman equation to approximate the finite-horizon using a batch expected hypervolume improvement (EHVI) acquisition function (AF) for MOO. Our formulation naturally allows us to use other improvement-based scalarizations and compare their efficacy to HVI. We derive three non-myopic AFs for MOBO: 1) the Nested AF, which is based on the exact computation of the lower bound, 2) the Joint AF, which is a lower bound on the nested AF, and 3) the BINOM AF, which is a fast and approximate variant based on batch multi-objective acquisition functions. Our experiments on multiple diverse real-world MO problems demonstrate that our non-myopic AFs substantially improve performance over the existing myopic AFs for MOBO.
Active Learning for Derivative-Based Global Sensitivity Analysis with Gaussian Processes
Jul 13, 2024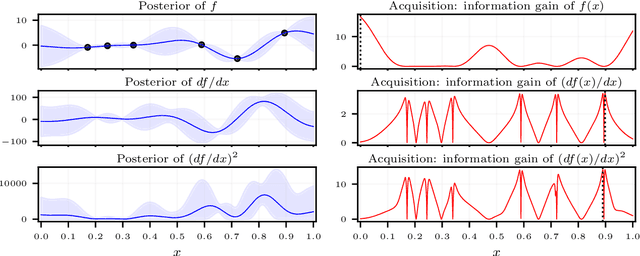
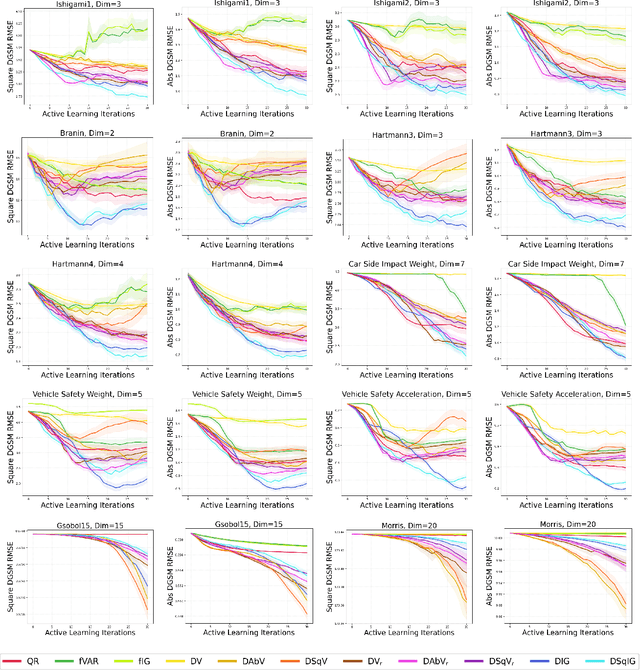
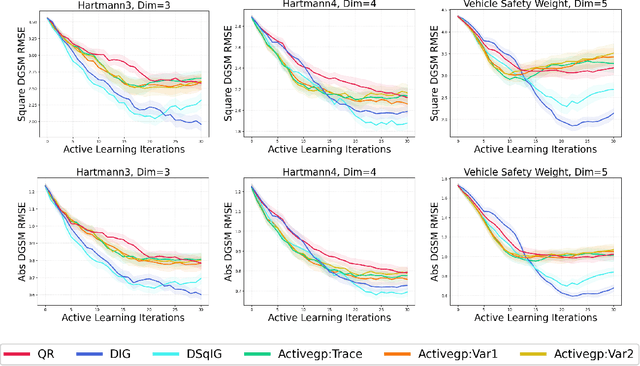
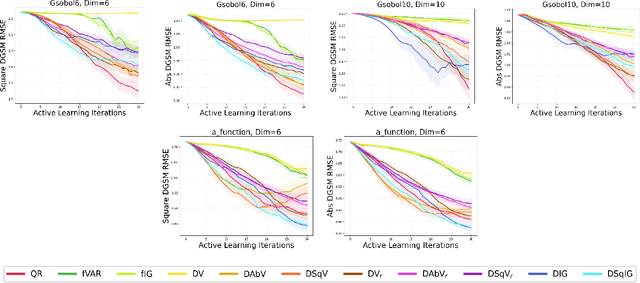
Abstract:We consider the problem of active learning for global sensitivity analysis of expensive black-box functions. Our aim is to efficiently learn the importance of different input variables, e.g., in vehicle safety experimentation, we study the impact of the thickness of various components on safety objectives. Since function evaluations are expensive, we use active learning to prioritize experimental resources where they yield the most value. We propose novel active learning acquisition functions that directly target key quantities of derivative-based global sensitivity measures (DGSMs) under Gaussian process surrogate models. We showcase the first application of active learning directly to DGSMs, and develop tractable uncertainty reduction and information gain acquisition functions for these measures. Through comprehensive evaluation on synthetic and real-world problems, our study demonstrates how these active learning acquisition strategies substantially enhance the sample efficiency of DGSM estimation, particularly with limited evaluation budgets. Our work paves the way for more efficient and accurate sensitivity analysis in various scientific and engineering applications.
Pareto Front-Diverse Batch Multi-Objective Bayesian Optimization
Jun 13, 2024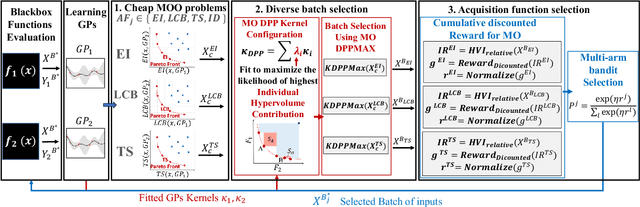
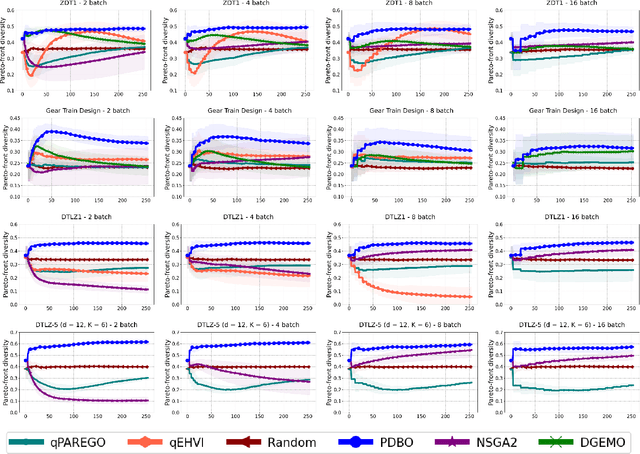
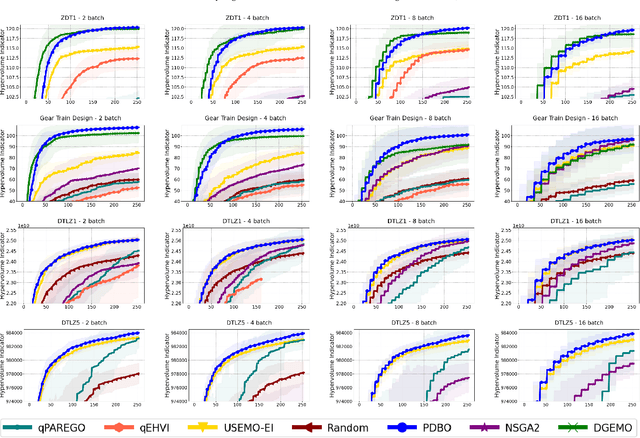
Abstract:We consider the problem of multi-objective optimization (MOO) of expensive black-box functions with the goal of discovering high-quality and diverse Pareto fronts where we are allowed to evaluate a batch of inputs. This problem arises in many real-world applications including penicillin production where diversity of solutions is critical. We solve this problem in the framework of Bayesian optimization (BO) and propose a novel approach referred to as Pareto front-Diverse Batch Multi-Objective BO (PDBO). PDBO tackles two important challenges: 1) How to automatically select the best acquisition function in each BO iteration, and 2) How to select a diverse batch of inputs by considering multiple objectives. We propose principled solutions to address these two challenges. First, PDBO employs a multi-armed bandit approach to select one acquisition function from a given library. We solve a cheap MOO problem by assigning the selected acquisition function for each expensive objective function to obtain a candidate set of inputs for evaluation. Second, it utilizes Determinantal Point Processes (DPPs) to choose a Pareto-front-diverse batch of inputs for evaluation from the candidate set obtained from the first step. The key parameters for the methods behind these two steps are updated after each round of function evaluations. Experiments on multiple MOO benchmarks demonstrate that PDBO outperforms prior methods in terms of both the quality and diversity of Pareto solutions.
Preference-Aware Constrained Multi-Objective Bayesian Optimization
Mar 23, 2023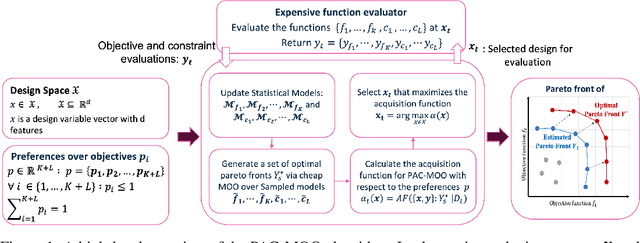
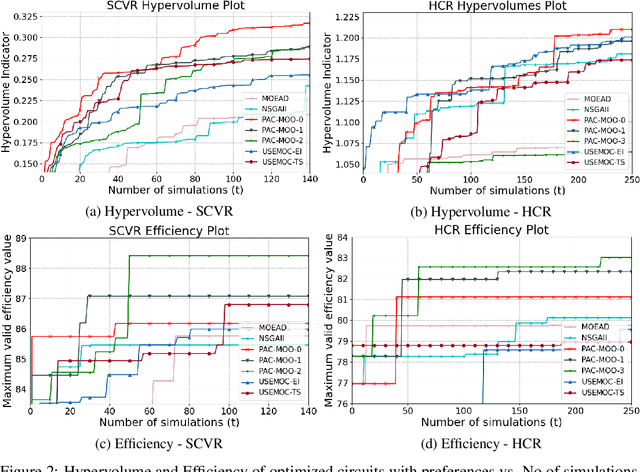
Abstract:This paper addresses the problem of constrained multi-objective optimization over black-box objective functions with practitioner-specified preferences over the objectives when a large fraction of the input space is infeasible (i.e., violates constraints). This problem arises in many engineering design problems including analog circuits and electric power system design. Our overall goal is to approximate the optimal Pareto set over the small fraction of feasible input designs. The key challenges include the huge size of the design space, multiple objectives and large number of constraints, and the small fraction of feasible input designs which can be identified only after performing expensive simulations. We propose a novel and efficient preference-aware constrained multi-objective Bayesian optimization approach referred to as PAC-MOO to address these challenges. The key idea is to learn surrogate models for both output objectives and constraints, and select the candidate input for evaluation in each iteration that maximizes the information gained about the optimal constrained Pareto front while factoring in the preferences over objectives. Our experiments on two real-world analog circuit design optimization problems demonstrate the efficacy of PAC-MOO over prior methods.
Bayesian Optimization Over Iterative Learners with Structured Responses: A Budget-aware Planning Approach
Jun 25, 2022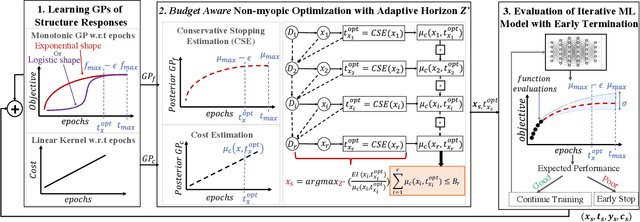
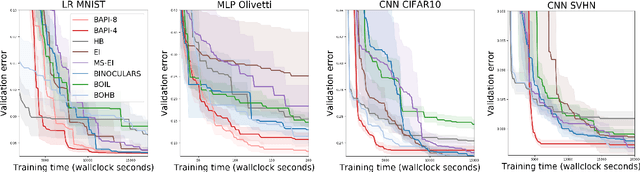
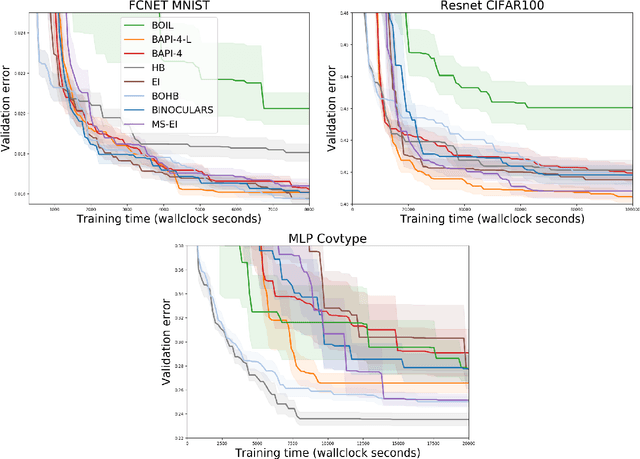
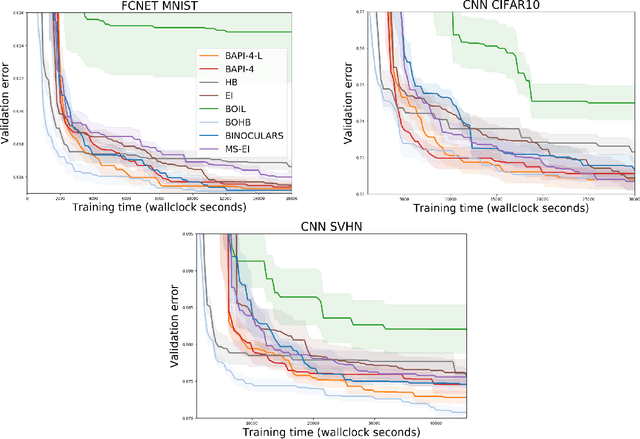
Abstract:The rising growth of deep neural networks (DNNs) and datasets in size motivates the need for efficient solutions for simultaneous model selection and training. Many methods for hyperparameter optimization (HPO) of iterative learners including DNNs attempt to solve this problem by querying and learning a response surface while searching for the optimum of that surface. However, many of these methods make myopic queries, do not consider prior knowledge about the response structure, and/or perform biased cost-aware search, all of which exacerbate identifying the best-performing model when a total cost budget is specified. This paper proposes a novel approach referred to as Budget-Aware Planning for Iterative Learners (BAPI) to solve HPO problems under a constrained cost budget. BAPI is an efficient non-myopic Bayesian optimization solution that accounts for the budget and leverages the prior knowledge about the objective function and cost function to select better configurations and to take more informed decisions during the evaluation (training). Experiments on diverse HPO benchmarks for iterative learners show that BAPI performs better than state-of-the-art baselines in most of the cases.
Uncertainty-Aware Search Framework for Multi-Objective Bayesian Optimization
Apr 12, 2022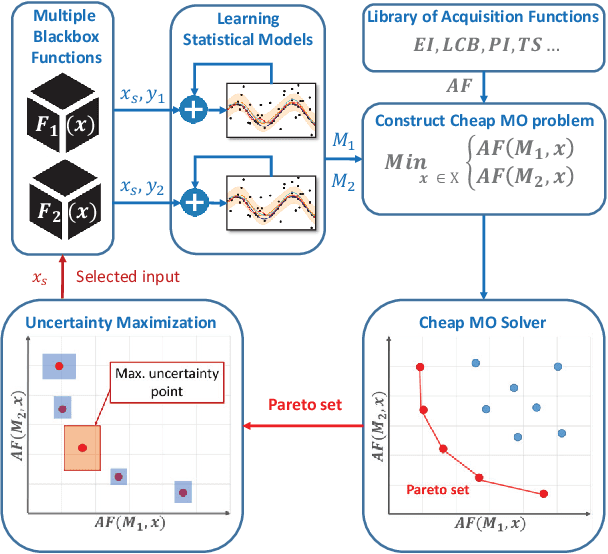
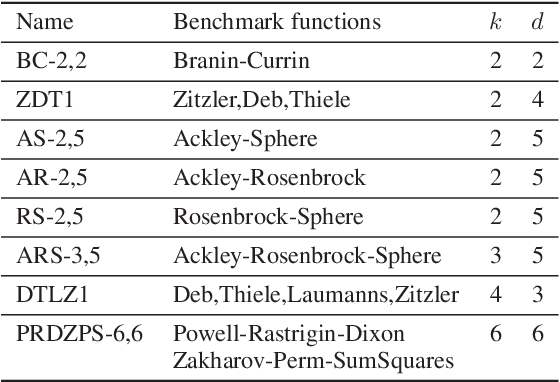
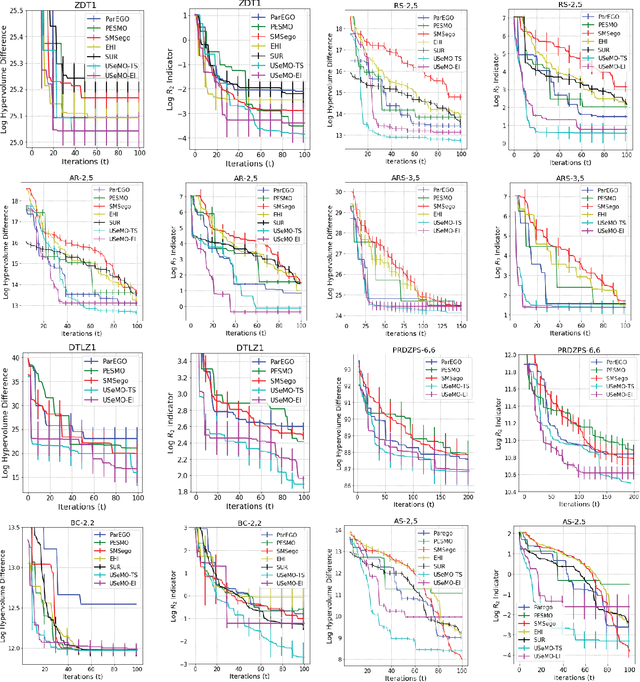
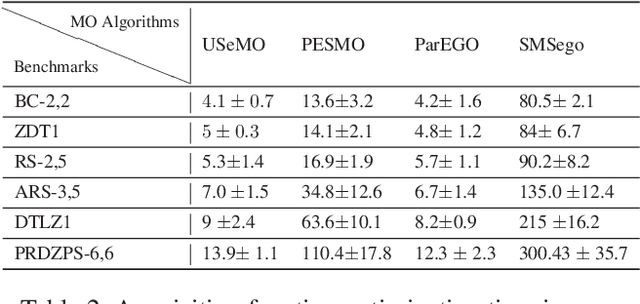
Abstract:We consider the problem of multi-objective (MO) blackbox optimization using expensive function evaluations, where the goal is to approximate the true Pareto set of solutions while minimizing the number of function evaluations. For example, in hardware design optimization, we need to find the designs that trade-off performance, energy, and area overhead using expensive simulations. We propose a novel uncertainty-aware search framework referred to as USeMO to efficiently select the sequence of inputs for evaluation to solve this problem. The selection method of USeMO consists of solving a cheap MO optimization problem via surrogate models of the true functions to identify the most promising candidates and picking the best candidate based on a measure of uncertainty. We also provide theoretical analysis to characterize the efficacy of our approach. Our experiments on several synthetic and six diverse real-world benchmark problems show that USeMO consistently outperforms the state-of-the-art algorithms.
* Added link to code and missing appendix. arXiv admin note: substantial text overlap with arXiv:2008.07029
Bayesian Optimization over Permutation Spaces
Dec 02, 2021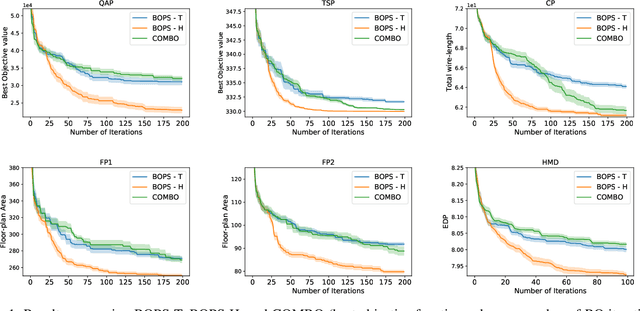
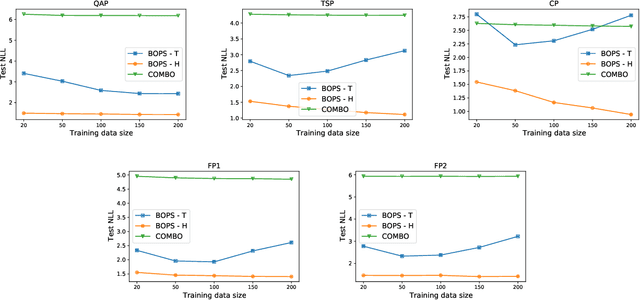
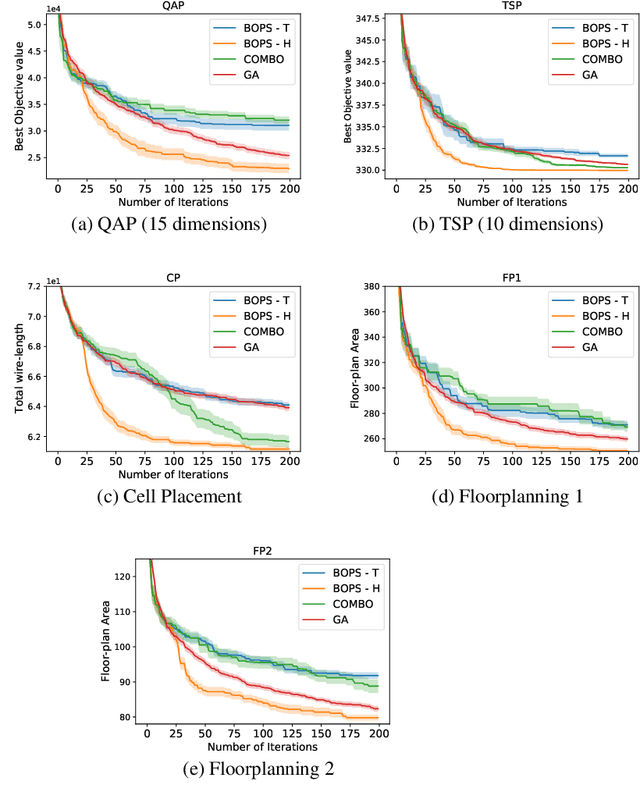
Abstract:Optimizing expensive to evaluate black-box functions over an input space consisting of all permutations of d objects is an important problem with many real-world applications. For example, placement of functional blocks in hardware design to optimize performance via simulations. The overall goal is to minimize the number of function evaluations to find high-performing permutations. The key challenge in solving this problem using the Bayesian optimization (BO) framework is to trade-off the complexity of statistical model and tractability of acquisition function optimization. In this paper, we propose and evaluate two algorithms for BO over Permutation Spaces (BOPS). First, BOPS-T employs Gaussian process (GP) surrogate model with Kendall kernels and a Tractable acquisition function optimization approach based on Thompson sampling to select the sequence of permutations for evaluation. Second, BOPS-H employs GP surrogate model with Mallow kernels and a Heuristic search approach to optimize expected improvement acquisition function. We theoretically analyze the performance of BOPS-T to show that their regret grows sub-linearly. Our experiments on multiple synthetic and real-world benchmarks show that both BOPS-T and BOPS-H perform better than the state-of-the-art BO algorithm for combinatorial spaces. To drive future research on this important problem, we make new resources and real-world benchmarks available to the community.
Output Space Entropy Search Framework for Multi-Objective Bayesian Optimization
Nov 03, 2021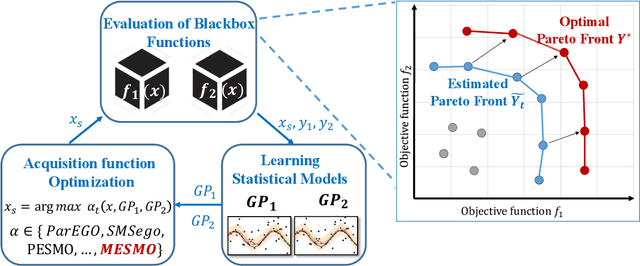
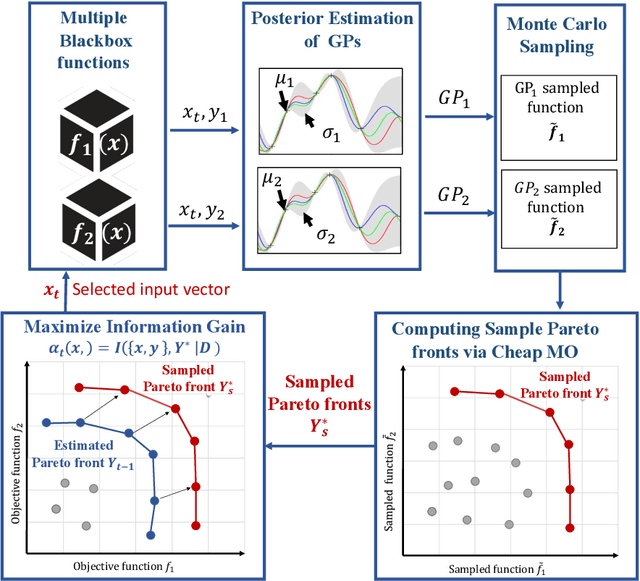
Abstract:We consider the problem of black-box multi-objective optimization (MOO) using expensive function evaluations (also referred to as experiments), where the goal is to approximate the true Pareto set of solutions by minimizing the total resource cost of experiments. For example, in hardware design optimization, we need to find the designs that trade-off performance, energy, and area overhead using expensive computational simulations. The key challenge is to select the sequence of experiments to uncover high-quality solutions using minimal resources. In this paper, we propose a general framework for solving MOO problems based on the principle of output space entropy (OSE) search: select the experiment that maximizes the information gained per unit resource cost about the true Pareto front. We appropriately instantiate the principle of OSE search to derive efficient algorithms for the following four MOO problem settings: 1) The most basic em single-fidelity setting, where experiments are expensive and accurate; 2) Handling em black-box constraints} which cannot be evaluated without performing experiments; 3) The discrete multi-fidelity setting, where experiments can vary in the amount of resources consumed and their evaluation accuracy; and 4) The em continuous-fidelity setting, where continuous function approximations result in a huge space of experiments. Experiments on diverse synthetic and real-world benchmarks show that our OSE search based algorithms improve over state-of-the-art methods in terms of both computational-efficiency and accuracy of MOO solutions.
* Accepted to Journal of Artificial Intelligence Research. arXiv admin note: substantial text overlap with arXiv:2009.05700, arXiv:2009.01721, arXiv:2011.01542
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge