Bayesian Optimization Over Iterative Learners with Structured Responses: A Budget-aware Planning Approach

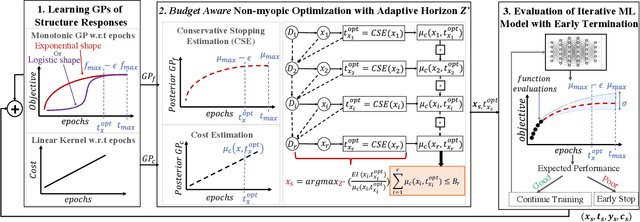
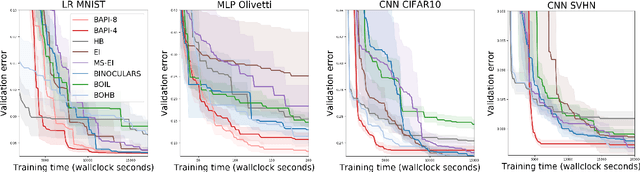
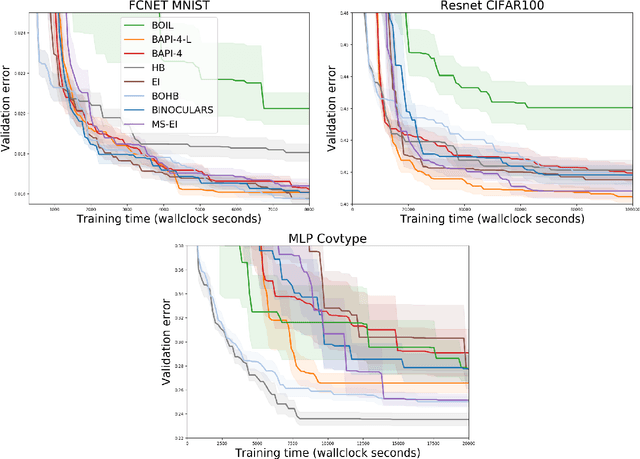
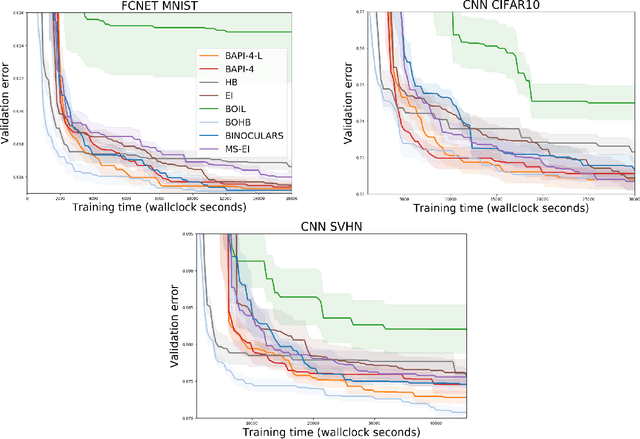
The rising growth of deep neural networks (DNNs) and datasets in size motivates the need for efficient solutions for simultaneous model selection and training. Many methods for hyperparameter optimization (HPO) of iterative learners including DNNs attempt to solve this problem by querying and learning a response surface while searching for the optimum of that surface. However, many of these methods make myopic queries, do not consider prior knowledge about the response structure, and/or perform biased cost-aware search, all of which exacerbate identifying the best-performing model when a total cost budget is specified. This paper proposes a novel approach referred to as Budget-Aware Planning for Iterative Learners (BAPI) to solve HPO problems under a constrained cost budget. BAPI is an efficient non-myopic Bayesian optimization solution that accounts for the budget and leverages the prior knowledge about the objective function and cost function to select better configurations and to take more informed decisions during the evaluation (training). Experiments on diverse HPO benchmarks for iterative learners show that BAPI performs better than state-of-the-art baselines in most of the cases.

Direct loss minimization for sparse Gaussian processes

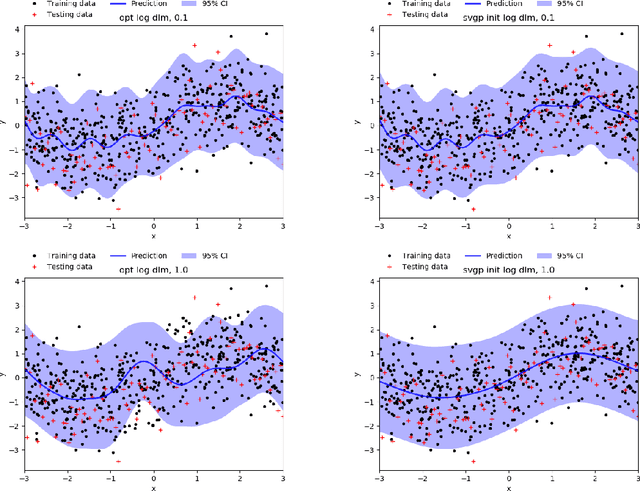
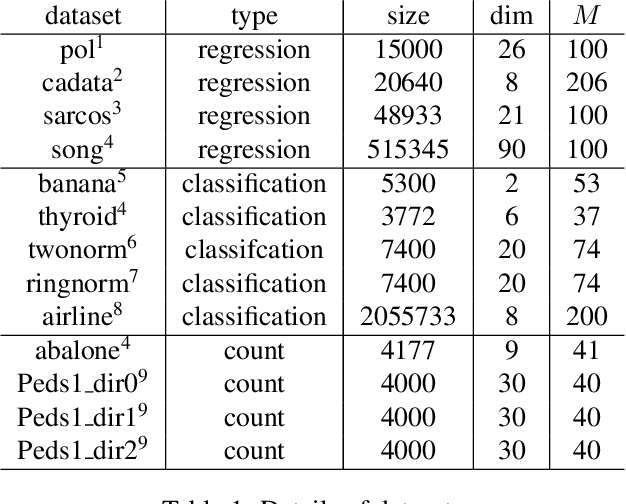
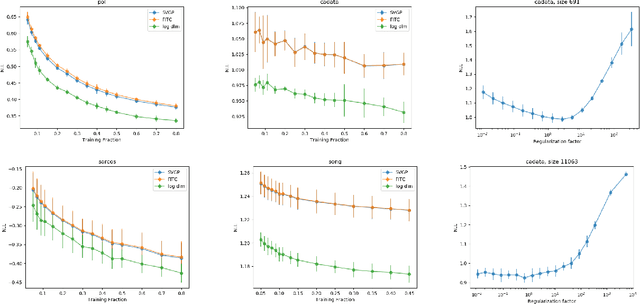
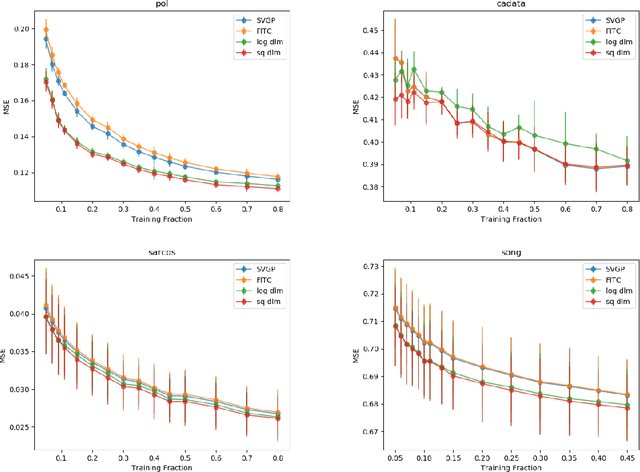
The Gaussian process (GP) is an attractive Bayesian model for machine learning which combines an elegant formulation with model flexibility and uncertainty quantification. Sparse Gaussian process (sGP) algorithms provide an approximate solution that mitigates the high computational complexity of GP and the variational approximation is the current best practice for such approximations. Recent theoretical work has shown that an alternative approach, direct loss minimization (DLM), which directly minimizes predictive loss, comes with strong guarantees on the expected loss of the algorithm. In this paper we explore this approach experimentally. We develop the DLM algorithm for sGP and show that with appropriate hyperparameter optimization it provides a significant improvement over the variational approach. In particular, optimizing sGP for log loss provides better calibrated predictions for regression, classification and count prediction, and optimizing sGP for square loss improves the mean square error in regression.

Weighted Meta-Learning

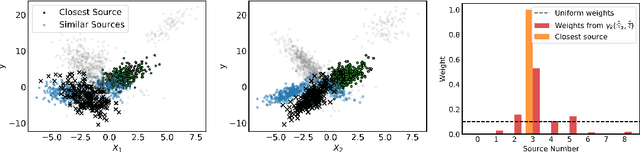
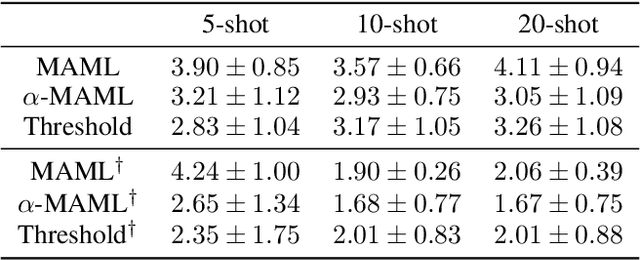
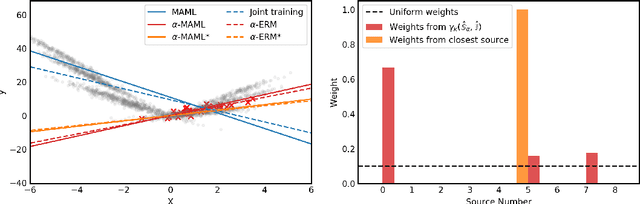
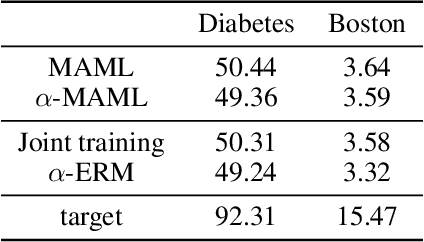
Meta-learning leverages related source tasks to learn an initialization that can be quickly fine-tuned to a target task with limited labeled examples. However, many popular meta-learning algorithms, such as model-agnostic meta-learning (MAML), only assume access to the target samples for fine-tuning. In this work, we provide a general framework for meta-learning based on weighting the loss of different source tasks, where the weights are allowed to depend on the target samples. In this general setting, we provide upper bounds on the distance of the weighted empirical risk of the source tasks and expected target risk in terms of an integral probability metric (IPM) and Rademacher complexity, which apply to a number of meta-learning settings including MAML and a weighted MAML variant. We then develop a learning algorithm based on minimizing the error bound with respect to an empirical IPM, including a weighted MAML algorithm, $\alpha$-MAML. Finally, we demonstrate empirically on several regression problems that our weighted meta-learning algorithm is able to find better initializations than uniformly-weighted meta-learning algorithms, such as MAML.

Feature Gradients: Scalable Feature Selection via Discrete Relaxation

In this paper we introduce Feature Gradients, a gradient-based search algorithm for feature selection. Our approach extends a recent result on the estimation of learnability in the sublinear data regime by showing that the calculation can be performed iteratively (i.e., in mini-batches) and in linear time and space with respect to both the number of features D and the sample size N . This, along with a discrete-to-continuous relaxation of the search domain, allows for an efficient, gradient-based search algorithm among feature subsets for very large datasets. Crucially, our algorithm is capable of finding higher-order correlations between features and targets for both the N > D and N < D regimes, as opposed to approaches that do not consider such interactions and/or only consider one regime. We provide experimental demonstration of the algorithm in small and large sample-and feature-size settings.

Probabilistic Matrix Factorization for Automated Machine Learning

In order to achieve state-of-the-art performance, modern machine learning techniques require careful data pre-processing and hyperparameter tuning. Moreover, given the ever increasing number of machine learning models being developed, model selection is becoming increasingly important. Automating the selection and tuning of machine learning pipelines consisting of data pre-processing methods and machine learning models, has long been one of the goals of the machine learning community. In this paper, we tackle this meta-learning task by combining ideas from collaborative filtering and Bayesian optimization. Using probabilistic matrix factorization techniques and acquisition functions from Bayesian optimization, we exploit experiments performed in hundreds of different datasets to guide the exploration of the space of possible pipelines. In our experiments, we show that our approach quickly identifies high-performing pipelines across a wide range of datasets, significantly outperforming the current state-of-the-art.

Monte Carlo Structured SVI for Two-Level Non-Conjugate Models

The stochastic variational inference (SVI) paradigm, which combines variational inference, natural gradients, and stochastic updates, was recently proposed for large-scale data analysis in conjugate Bayesian models and demonstrated to be effective in several problems. This paper studies a family of Bayesian latent variable models with two levels of hidden variables but without any conjugacy requirements, making several contributions in this context. The first is observing that SVI, with an improved structured variational approximation, is applicable under more general conditions than previously thought with the only requirement being that the approximating variational distribution be in the same family as the prior. The resulting approach, Monte Carlo Structured SVI (MC-SSVI), significantly extends the scope of SVI, enabling large-scale learning in non-conjugate models. For models with latent Gaussian variables we propose a hybrid algorithm, using both standard and natural gradients, which is shown to improve stability and convergence. Applications in mixed effects models, sparse Gaussian processes, probabilistic matrix factorization and correlated topic models demonstrate the generality of the approach and the advantages of the proposed algorithms.