Direct loss minimization for sparse Gaussian processes

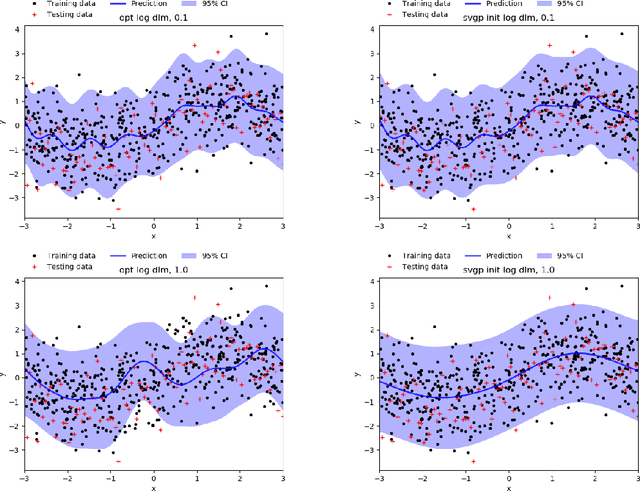
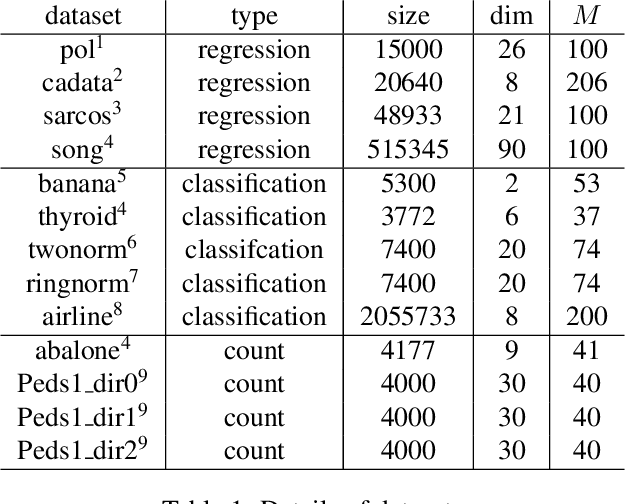
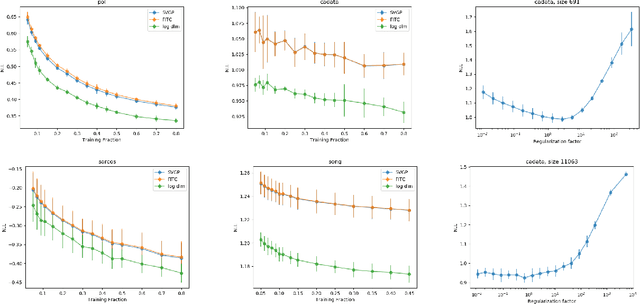
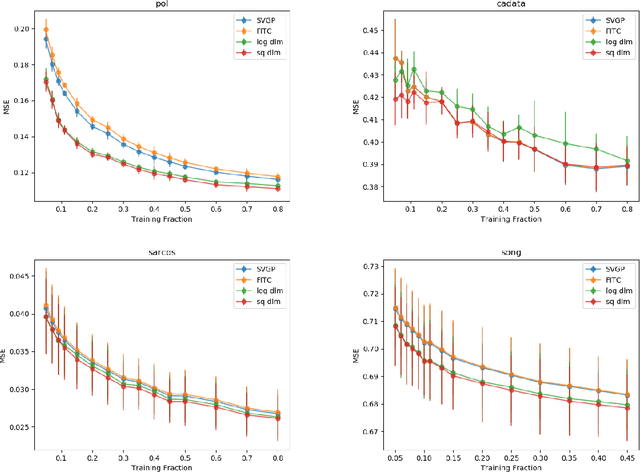
The Gaussian process (GP) is an attractive Bayesian model for machine learning which combines an elegant formulation with model flexibility and uncertainty quantification. Sparse Gaussian process (sGP) algorithms provide an approximate solution that mitigates the high computational complexity of GP and the variational approximation is the current best practice for such approximations. Recent theoretical work has shown that an alternative approach, direct loss minimization (DLM), which directly minimizes predictive loss, comes with strong guarantees on the expected loss of the algorithm. In this paper we explore this approach experimentally. We develop the DLM algorithm for sGP and show that with appropriate hyperparameter optimization it provides a significant improvement over the variational approach. In particular, optimizing sGP for log loss provides better calibrated predictions for regression, classification and count prediction, and optimizing sGP for square loss improves the mean square error in regression.