POAM: Probabilistic Online Attentive Mapping for Efficient Robotic Information Gathering

Gaussian Process (GP) models are widely used for Robotic Information Gathering (RIG) in exploring unknown environments due to their ability to model complex phenomena with non-parametric flexibility and accurately quantify prediction uncertainty. Previous work has developed informative planners and adaptive GP models to enhance the data efficiency of RIG by improving the robot's sampling strategy to focus on informative regions in non-stationary environments. However, computational efficiency becomes a bottleneck when using GP models in large-scale environments with limited computational resources. We propose a framework -- Probabilistic Online Attentive Mapping (POAM) -- that leverages the modeling strengths of the non-stationary Attentive Kernel while achieving constant-time computational complexity for online decision-making. POAM guides the optimization process via variational Expectation Maximization, providing constant-time update rules for inducing inputs, variational parameters, and hyperparameters. Extensive experiments in active bathymetric mapping tasks demonstrate that POAM significantly improves computational efficiency, model accuracy, and uncertainty quantification capability compared to existing online sparse GP models.

Adaptive Robotic Information Gathering via Non-Stationary Gaussian Processes

Robotic Information Gathering (RIG) is a foundational research topic that answers how a robot (team) collects informative data to efficiently build an accurate model of an unknown target function under robot embodiment constraints. RIG has many applications, including but not limited to autonomous exploration and mapping, 3D reconstruction or inspection, search and rescue, and environmental monitoring. A RIG system relies on a probabilistic model's prediction uncertainty to identify critical areas for informative data collection. Gaussian Processes (GPs) with stationary kernels have been widely adopted for spatial modeling. However, real-world spatial data is typically non-stationary -- different locations do not have the same degree of variability. As a result, the prediction uncertainty does not accurately reveal prediction error, limiting the success of RIG algorithms. We propose a family of non-stationary kernels named Attentive Kernel (AK), which is simple, robust, and can extend any existing kernel to a non-stationary one. We evaluate the new kernel in elevation mapping tasks, where AK provides better accuracy and uncertainty quantification over the commonly used stationary kernels and the leading non-stationary kernels. The improved uncertainty quantification guides the downstream informative planner to collect more valuable data around the high-error area, further increasing prediction accuracy. A field experiment demonstrates that the proposed method can guide an Autonomous Surface Vehicle (ASV) to prioritize data collection in locations with significant spatial variations, enabling the model to characterize salient environmental features.

Direct Uncertainty Quantification

Traditional neural networks are simple to train but they produce overconfident predictions, while Bayesian neural networks provide good uncertainty quantification but optimizing them is time consuming. This paper introduces a new approach, direct uncertainty quantification (DirectUQ), that combines their advantages where the neural network directly models uncertainty in output space, and captures both aleatoric and epistemic uncertainty. DirectUQ can be derived as an alternative variational lower bound, and hence benefits from collapsed variational inference that provides improved regularizers. On the other hand, like non-probabilistic models, DirectUQ enjoys simple training and one can use Rademacher complexity to provide risk bounds for the model. Experiments show that DirectUQ and ensembles of DirectUQ provide a good tradeoff in terms of run time and uncertainty quantification, especially for out of distribution data.

DiSProD: Differentiable Symbolic Propagation of Distributions for Planning

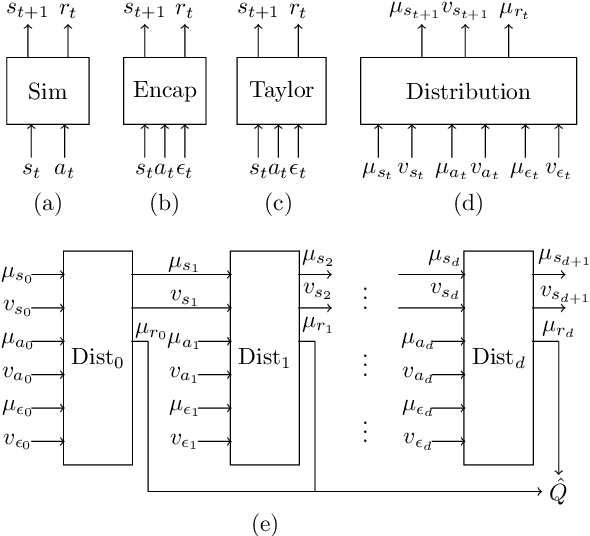
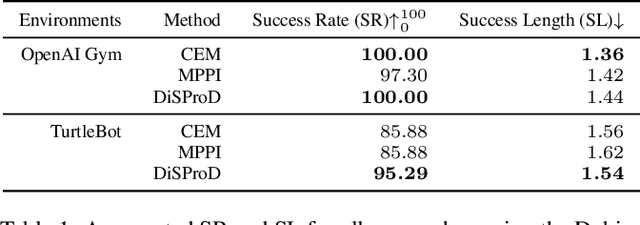
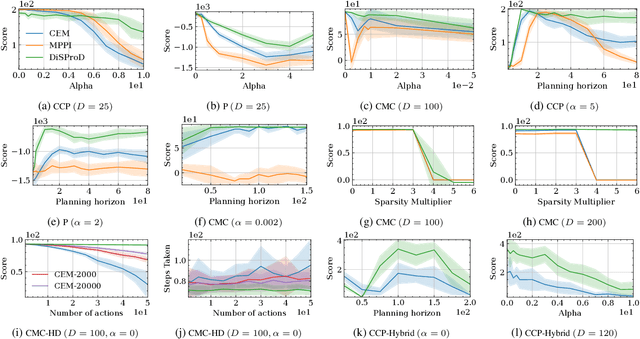
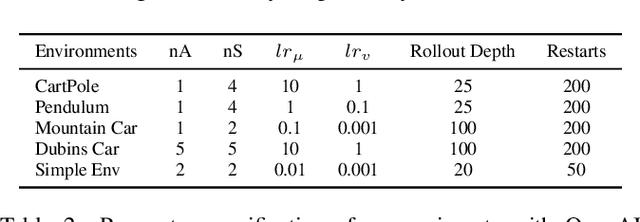
The paper introduces DiSProD, an online planner developed for environments with probabilistic transitions in continuous state and action spaces. DiSProD builds a symbolic graph that captures the distribution of future trajectories, conditioned on a given policy, using independence assumptions and approximate propagation of distributions. The symbolic graph provides a differentiable representation of the policy's value, enabling efficient gradient-based optimization for long-horizon search. The propagation of approximate distributions can be seen as an aggregation of many trajectories, making it well-suited for dealing with sparse rewards and stochastic environments. An extensive experimental evaluation compares DiSProD to state-of-the-art planners in discrete-time planning and real-time control of robotic systems. The proposed method improves over existing planners in handling stochastic environments, sensitivity to search depth, sparsity of rewards, and large action spaces. Additional real-world experiments demonstrate that DiSProD can control ground vehicles and surface vessels to successfully navigate around obstacles.

On the Performance of Direct Loss Minimization for Bayesian Neural Networks

Direct Loss Minimization (DLM) has been proposed as a pseudo-Bayesian method motivated as regularized loss minimization. Compared to variational inference, it replaces the loss term in the evidence lower bound (ELBO) with the predictive log loss, which is the same loss function used in evaluation. A number of theoretical and empirical results in prior work suggest that DLM can significantly improve over ELBO optimization for some models. However, as we point out in this paper, this is not the case for Bayesian neural networks (BNNs). The paper explores the practical performance of DLM for BNN, the reasons for its failure and its relationship to optimizing the ELBO, uncovering some interesting facts about both algorithms.

Explainable Models via Compression of Tree Ensembles

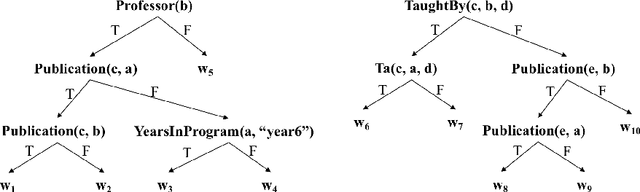
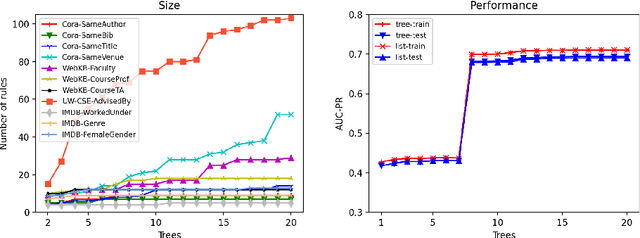
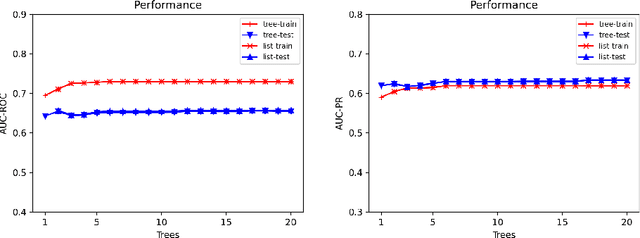
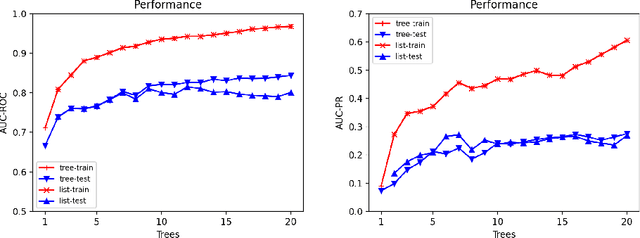
Ensemble models (bagging and gradient-boosting) of relational decision trees have proved to be one of the most effective learning methods in the area of probabilistic logic models (PLMs). While effective, they lose one of the most important aspect of PLMs -- interpretability. In this paper we consider the problem of compressing a large set of learned trees into a single explainable model. To this effect, we propose CoTE -- Compression of Tree Ensembles -- that produces a single small decision list as a compressed representation. CoTE first converts the trees to decision lists and then performs the combination and compression with the aid of the original training set. An experimental evaluation demonstrates the effectiveness of CoTE in several benchmark relational data sets.

AK: Attentive Kernel for Information Gathering

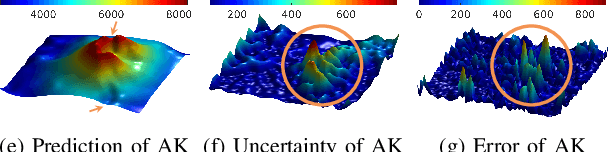
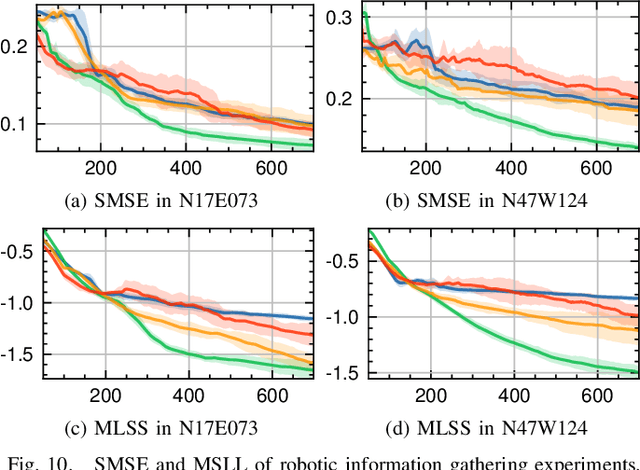
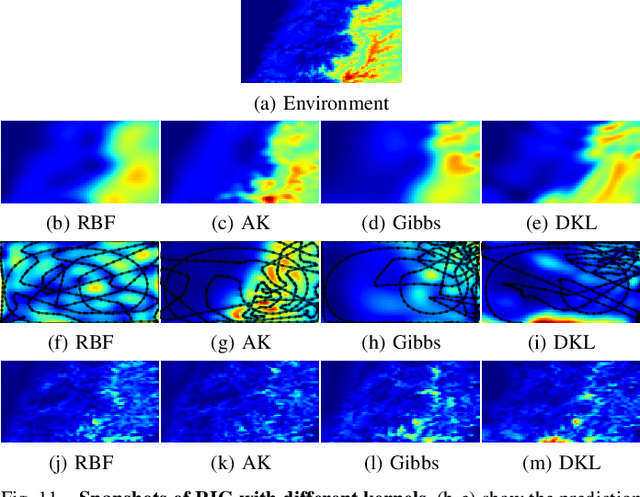
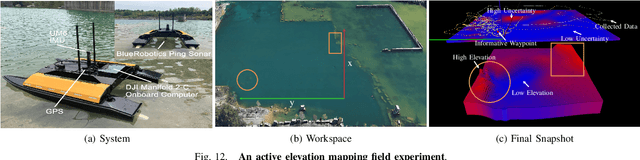
Robotic Information Gathering (RIG) relies on the uncertainty of a probabilistic model to identify critical areas for efficient data collection. Gaussian processes (GPs) with stationary kernels have been widely adopted for spatial modeling. However, real-world spatial data typically does not satisfy the assumption of stationarity, where different locations are assumed to have the same degree of variability. As a result, the prediction uncertainty does not accurately capture prediction error, limiting the success of RIG algorithms. We propose a novel family of nonstationary kernels, named the Attentive Kernel (AK), which is simple, robust, and can extend any existing kernel to a nonstationary one. We evaluate the new kernel in elevation mapping tasks, where AK provides better accuracy and uncertainty quantification over the commonly used RBF kernel and other popular nonstationary kernels. The improved uncertainty quantification guides the downstream RIG planner to collect more valuable data around the high-error area, further increasing prediction accuracy. A field experiment demonstrates that the proposed method can guide an Autonomous Surface Vehicle (ASV) to prioritize data collection in locations with high spatial variations, enabling the model to characterize the salient environmental features.

Approximate Inference for Stochastic Planning in Factored Spaces

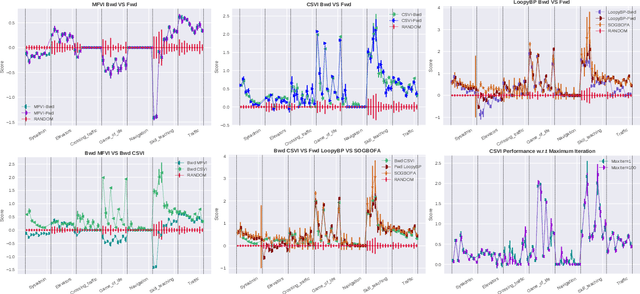
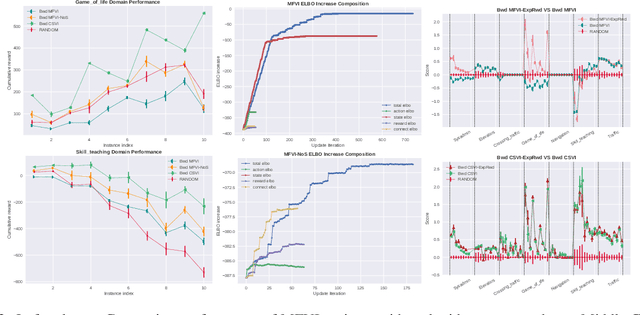
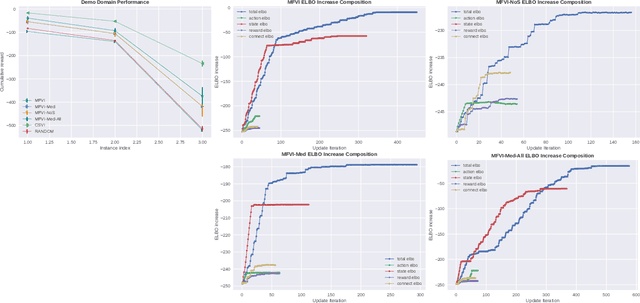
The paper explores the use of approximate inference techniques as solution methods for stochastic planning problems with discrete factored spaces. While much prior work exists on this topic, subtle variations hinder a global understanding of different approaches for their differences and potential advantages. Here we abstract a simple framework that captures and connects prior work along two dimensions, direction of information flow, i.e., forward vs backward inference, and the type of approximation used, e.g., Belief Propagation (BP) vs mean field variational inference (MFVI). Through this analysis we also propose a novel algorithm, CSVI, which provides a tighter variational approximation compared to prior work. An extensive experimental evaluation compares algorithms from different branches of the framework, showing that methods based on BP are generally better than methods based on MFVI, that CSVI is competitive with BP algorithms, and that while inference direction does not show a significant effect for VI methods, forward inference provides stronger performance with BP.

Direct loss minimization for sparse Gaussian processes

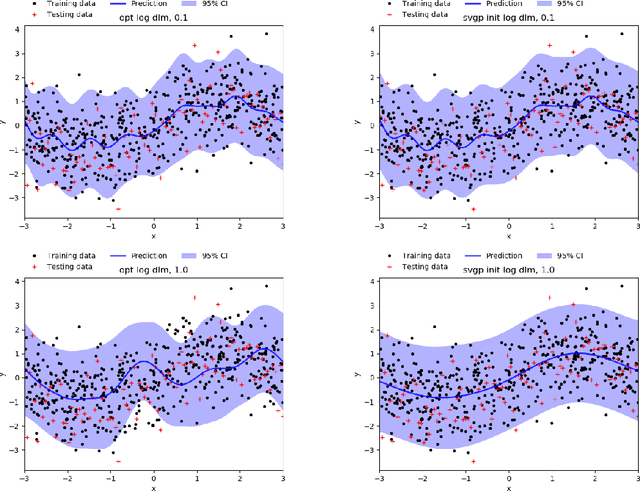
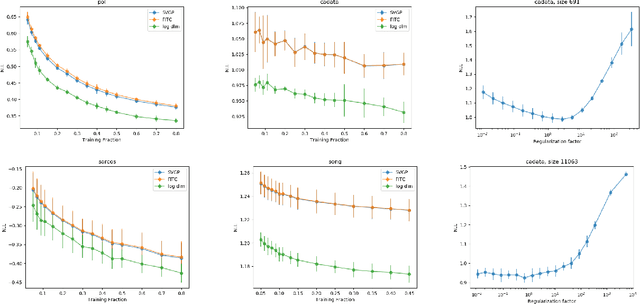
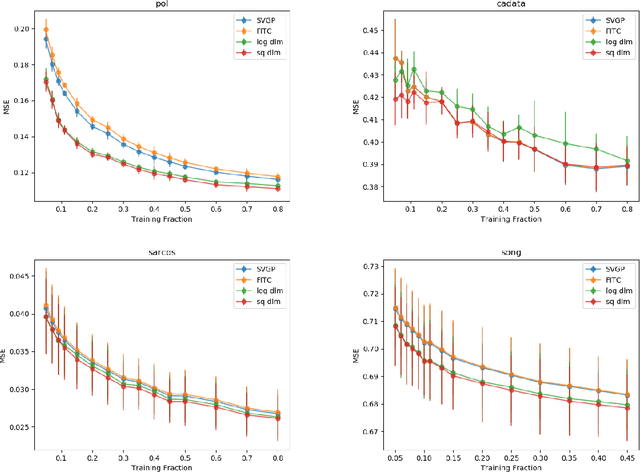
The Gaussian process (GP) is an attractive Bayesian model for machine learning which combines an elegant formulation with model flexibility and uncertainty quantification. Sparse Gaussian process (sGP) algorithms provide an approximate solution that mitigates the high computational complexity of GP and the variational approximation is the current best practice for such approximations. Recent theoretical work has shown that an alternative approach, direct loss minimization (DLM), which directly minimizes predictive loss, comes with strong guarantees on the expected loss of the algorithm. In this paper we explore this approach experimentally. We develop the DLM algorithm for sGP and show that with appropriate hyperparameter optimization it provides a significant improvement over the variational approach. In particular, optimizing sGP for log loss provides better calibrated predictions for regression, classification and count prediction, and optimizing sGP for square loss improves the mean square error in regression.

Monte Carlo Structured SVI for Two-Level Non-Conjugate Models

The stochastic variational inference (SVI) paradigm, which combines variational inference, natural gradients, and stochastic updates, was recently proposed for large-scale data analysis in conjugate Bayesian models and demonstrated to be effective in several problems. This paper studies a family of Bayesian latent variable models with two levels of hidden variables but without any conjugacy requirements, making several contributions in this context. The first is observing that SVI, with an improved structured variational approximation, is applicable under more general conditions than previously thought with the only requirement being that the approximating variational distribution be in the same family as the prior. The resulting approach, Monte Carlo Structured SVI (MC-SSVI), significantly extends the scope of SVI, enabling large-scale learning in non-conjugate models. For models with latent Gaussian variables we propose a hybrid algorithm, using both standard and natural gradients, which is shown to improve stability and convergence. Applications in mixed effects models, sparse Gaussian processes, probabilistic matrix factorization and correlated topic models demonstrate the generality of the approach and the advantages of the proposed algorithms.