Scaling laws in wearable human activity recognition

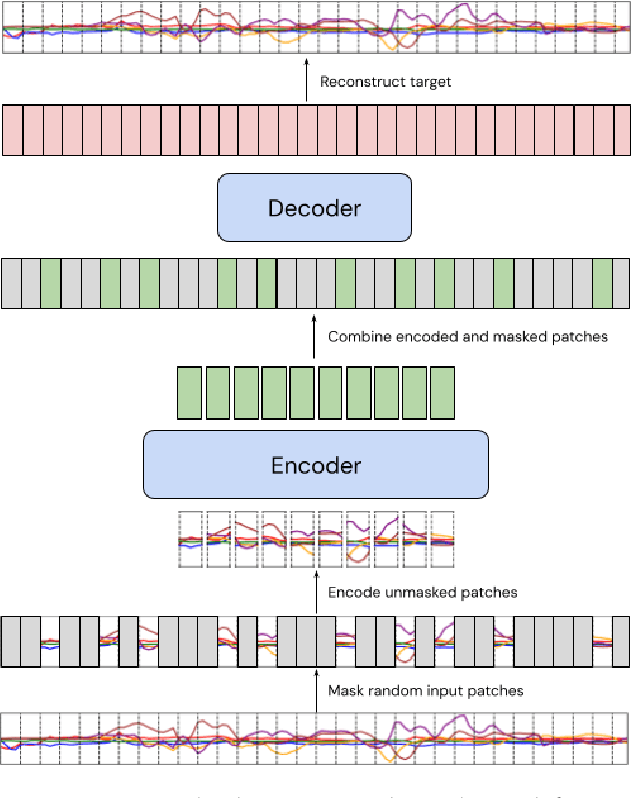
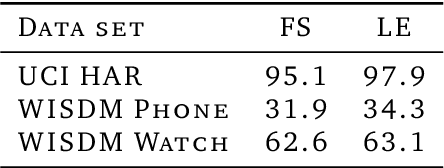
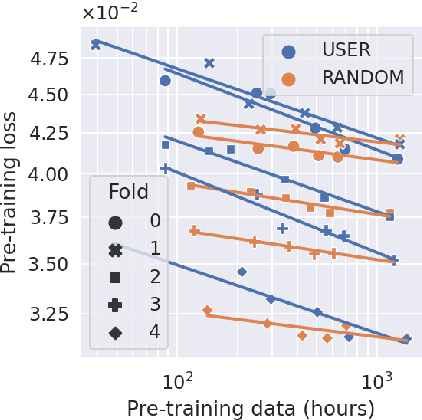
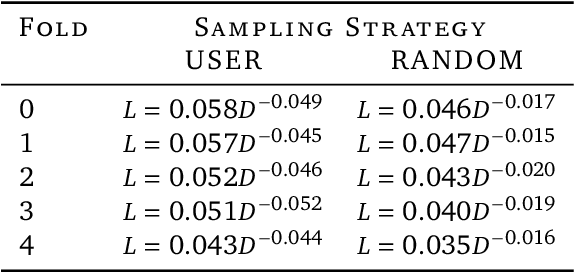
Many deep architectures and self-supervised pre-training techniques have been proposed for human activity recognition (HAR) from wearable multimodal sensors. Scaling laws have the potential to help move towards more principled design by linking model capacity with pre-training data volume. Yet, scaling laws have not been established for HAR to the same extent as in language and vision. By conducting an exhaustive grid search on both amount of pre-training data and Transformer architectures, we establish the first known scaling laws for HAR. We show that pre-training loss scales with a power law relationship to amount of data and parameter count and that increasing the number of users in a dataset results in a steeper improvement in performance than increasing data per user, indicating that diversity of pre-training data is important, which contrasts to some previously reported findings in self-supervised HAR. We show that these scaling laws translate to downstream performance improvements on three HAR benchmark datasets of postures, modes of locomotion and activities of daily living: UCI HAR and WISDM Phone and WISDM Watch. Finally, we suggest some previously published works should be revisited in light of these scaling laws with more adequate model capacities.

Explainable Models via Compression of Tree Ensembles

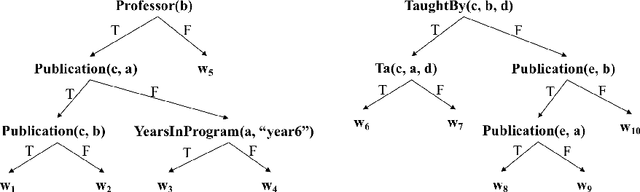
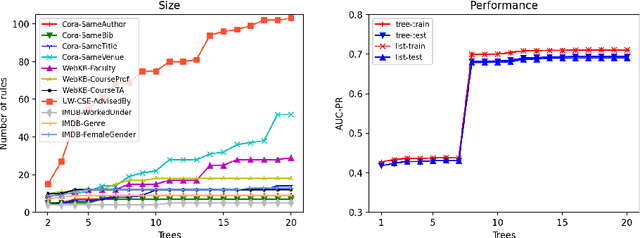
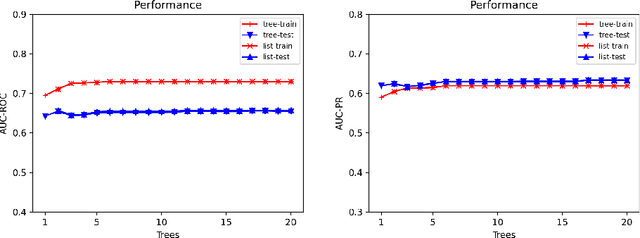
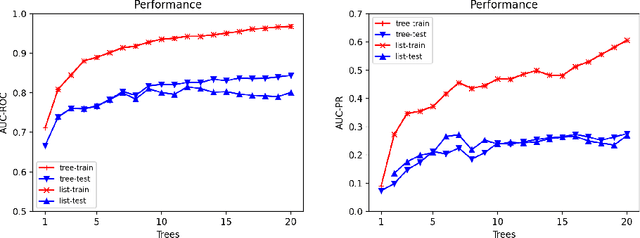
Ensemble models (bagging and gradient-boosting) of relational decision trees have proved to be one of the most effective learning methods in the area of probabilistic logic models (PLMs). While effective, they lose one of the most important aspect of PLMs -- interpretability. In this paper we consider the problem of compressing a large set of learned trees into a single explainable model. To this effect, we propose CoTE -- Compression of Tree Ensembles -- that produces a single small decision list as a compressed representation. CoTE first converts the trees to decision lists and then performs the combination and compression with the aid of the original training set. An experimental evaluation demonstrates the effectiveness of CoTE in several benchmark relational data sets.

Neural Networks for Relational Data

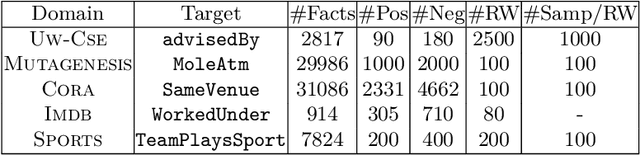
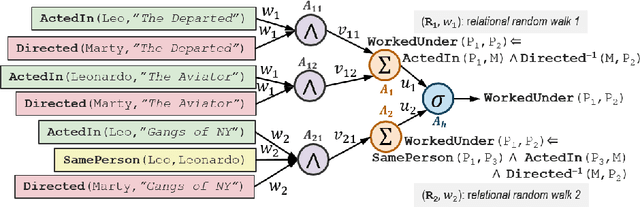
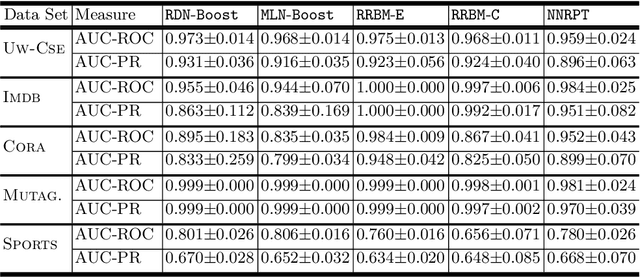
While deep networks have been enormously successful over the last decade, they rely on flat-feature vector representations, which makes them unsuitable for richly structured domains such as those arising in applications like social network analysis. Such domains rely on relational representations to capture complex relationships between entities and their attributes. Thus, we consider the problem of learning neural networks for relational data. We distinguish ourselves from current approaches that rely on expert hand-coded rules by learning relational random-walk-based features to capture local structural interactions and the resulting network architecture. We further exploit parameter tying of the network weights of the resulting relational neural network, where instances of the same type share parameters. Our experimental results across several standard relational data sets demonstrate the effectiveness of the proposed approach over multiple neural net baselines as well as state-of-the-art statistical relational models.

Probabilistic Relational Planning with First Order Decision Diagrams

Dynamic programming algorithms have been successfully applied to propositional stochastic planning problems by using compact representations, in particular algebraic decision diagrams, to capture domain dynamics and value functions. Work on symbolic dynamic programming lifted these ideas to first order logic using several representation schemes. Recent work introduced a first order variant of decision diagrams (FODD) and developed a value iteration algorithm for this representation. This paper develops several improvements to the FODD algorithm that make the approach practical. These include, new reduction operators that decrease the size of the representation, several speedup techniques, and techniques for value approximation. Incorporating these, the paper presents a planning system, FODD-Planner, for solving relational stochastic planning problems. The system is evaluated on several domains, including problems from the recent international planning competition, and shows competitive performance with top ranking systems. This is the first demonstration of feasibility of this approach and it shows that abstraction through compact representation is a promising approach to stochastic planning.

First Order Decision Diagrams for Relational MDPs

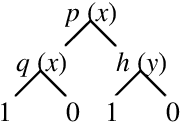
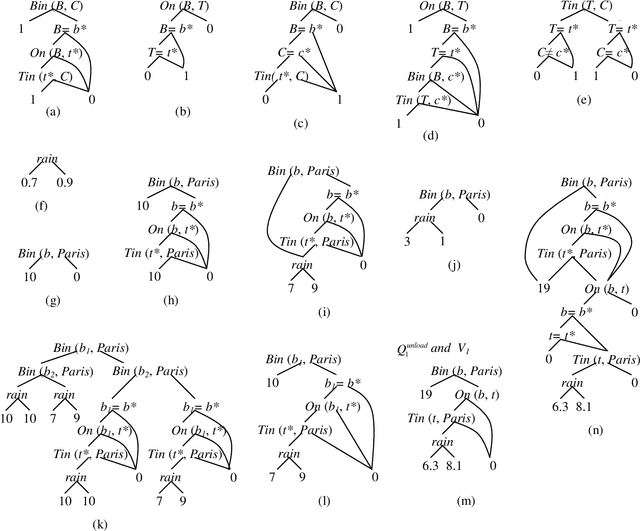
Markov decision processes capture sequential decision making under uncertainty, where an agent must choose actions so as to optimize long term reward. The paper studies efficient reasoning mechanisms for Relational Markov Decision Processes (RMDP) where world states have an internal relational structure that can be naturally described in terms of objects and relations among them. Two contributions are presented. First, the paper develops First Order Decision Diagrams (FODD), a new compact representation for functions over relational structures, together with a set of operators to combine FODDs, and novel reduction techniques to keep the representation small. Second, the paper shows how FODDs can be used to develop solutions for RMDPs, where reasoning is performed at the abstract level and the resulting optimal policy is independent of domain size (number of objects) or instantiation. In particular, a variant of the value iteration algorithm is developed by using special operations over FODDs, and the algorithm is shown to converge to the optimal policy.