Approximate Inference for Stochastic Planning in Factored Spaces

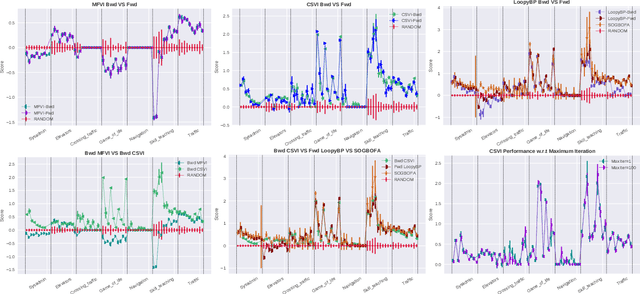
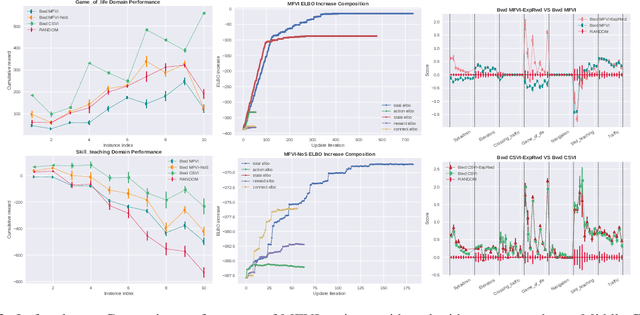
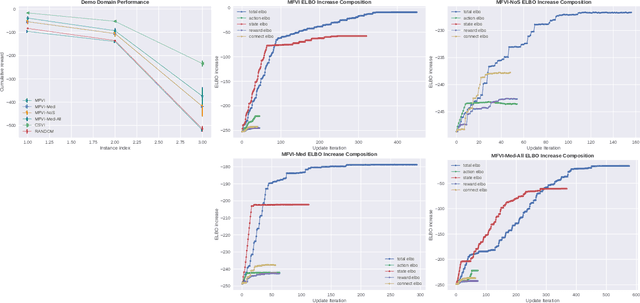
The paper explores the use of approximate inference techniques as solution methods for stochastic planning problems with discrete factored spaces. While much prior work exists on this topic, subtle variations hinder a global understanding of different approaches for their differences and potential advantages. Here we abstract a simple framework that captures and connects prior work along two dimensions, direction of information flow, i.e., forward vs backward inference, and the type of approximation used, e.g., Belief Propagation (BP) vs mean field variational inference (MFVI). Through this analysis we also propose a novel algorithm, CSVI, which provides a tighter variational approximation compared to prior work. An extensive experimental evaluation compares algorithms from different branches of the framework, showing that methods based on BP are generally better than methods based on MFVI, that CSVI is competitive with BP algorithms, and that while inference direction does not show a significant effect for VI methods, forward inference provides stronger performance with BP.