Direct Uncertainty Quantification

Traditional neural networks are simple to train but they produce overconfident predictions, while Bayesian neural networks provide good uncertainty quantification but optimizing them is time consuming. This paper introduces a new approach, direct uncertainty quantification (DirectUQ), that combines their advantages where the neural network directly models uncertainty in output space, and captures both aleatoric and epistemic uncertainty. DirectUQ can be derived as an alternative variational lower bound, and hence benefits from collapsed variational inference that provides improved regularizers. On the other hand, like non-probabilistic models, DirectUQ enjoys simple training and one can use Rademacher complexity to provide risk bounds for the model. Experiments show that DirectUQ and ensembles of DirectUQ provide a good tradeoff in terms of run time and uncertainty quantification, especially for out of distribution data.

On the Performance of Direct Loss Minimization for Bayesian Neural Networks

Direct Loss Minimization (DLM) has been proposed as a pseudo-Bayesian method motivated as regularized loss minimization. Compared to variational inference, it replaces the loss term in the evidence lower bound (ELBO) with the predictive log loss, which is the same loss function used in evaluation. A number of theoretical and empirical results in prior work suggest that DLM can significantly improve over ELBO optimization for some models. However, as we point out in this paper, this is not the case for Bayesian neural networks (BNNs). The paper explores the practical performance of DLM for BNN, the reasons for its failure and its relationship to optimizing the ELBO, uncovering some interesting facts about both algorithms.

Direct loss minimization for sparse Gaussian processes

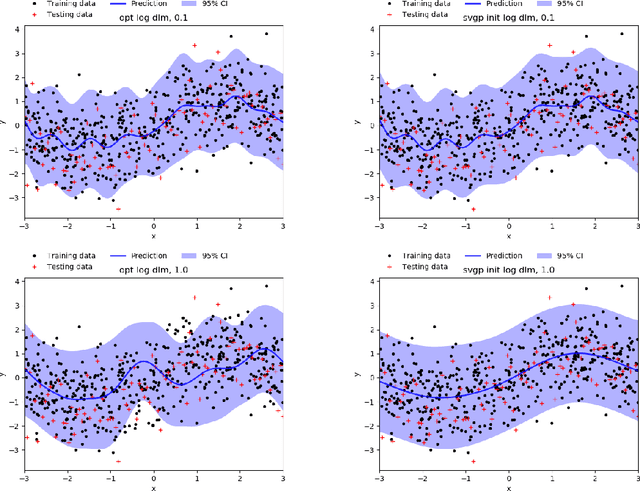
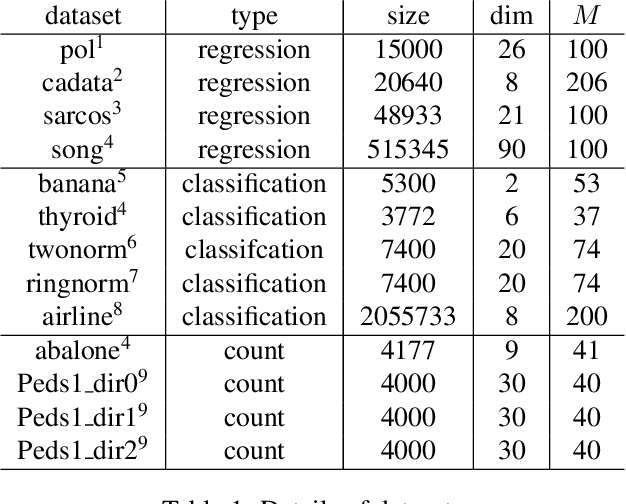
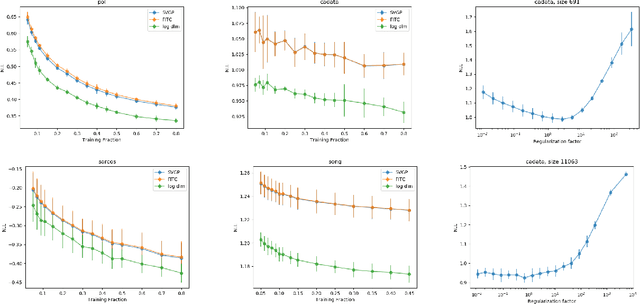
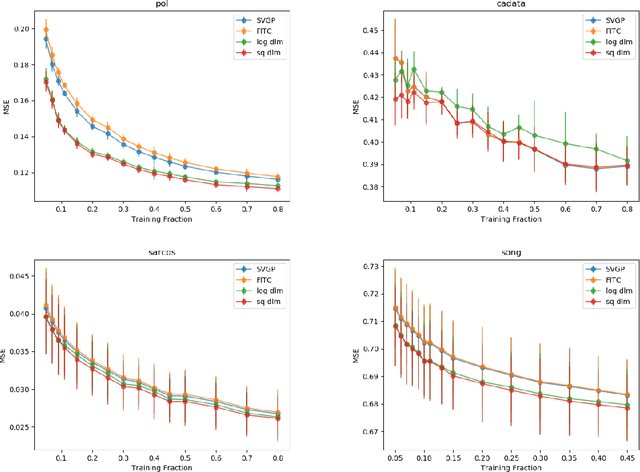
The Gaussian process (GP) is an attractive Bayesian model for machine learning which combines an elegant formulation with model flexibility and uncertainty quantification. Sparse Gaussian process (sGP) algorithms provide an approximate solution that mitigates the high computational complexity of GP and the variational approximation is the current best practice for such approximations. Recent theoretical work has shown that an alternative approach, direct loss minimization (DLM), which directly minimizes predictive loss, comes with strong guarantees on the expected loss of the algorithm. In this paper we explore this approach experimentally. We develop the DLM algorithm for sGP and show that with appropriate hyperparameter optimization it provides a significant improvement over the variational approach. In particular, optimizing sGP for log loss provides better calibrated predictions for regression, classification and count prediction, and optimizing sGP for square loss improves the mean square error in regression.