Weighted Meta-Learning
Paper and Code
Mar 20, 2020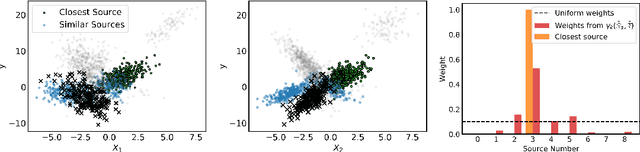
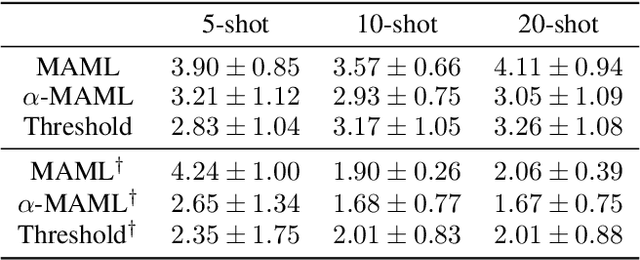
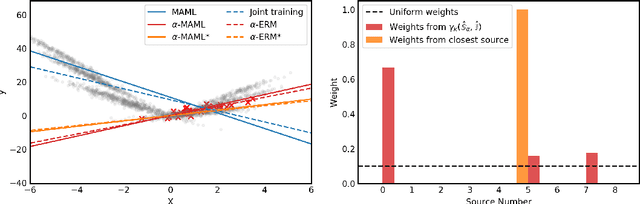
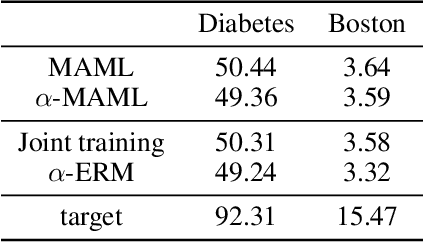
Meta-learning leverages related source tasks to learn an initialization that can be quickly fine-tuned to a target task with limited labeled examples. However, many popular meta-learning algorithms, such as model-agnostic meta-learning (MAML), only assume access to the target samples for fine-tuning. In this work, we provide a general framework for meta-learning based on weighting the loss of different source tasks, where the weights are allowed to depend on the target samples. In this general setting, we provide upper bounds on the distance of the weighted empirical risk of the source tasks and expected target risk in terms of an integral probability metric (IPM) and Rademacher complexity, which apply to a number of meta-learning settings including MAML and a weighted MAML variant. We then develop a learning algorithm based on minimizing the error bound with respect to an empirical IPM, including a weighted MAML algorithm, $\alpha$-MAML. Finally, we demonstrate empirically on several regression problems that our weighted meta-learning algorithm is able to find better initializations than uniformly-weighted meta-learning algorithms, such as MAML.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge