Non-Myopic Multi-Objective Bayesian Optimization

We consider the problem of finite-horizon sequential experimental design to solve multi-objective optimization (MOO) of expensive black-box objective functions. This problem arises in many real-world applications, including materials design, where we have a small resource budget to make and evaluate candidate materials in the lab. We solve this problem using the framework of Bayesian optimization (BO) and propose the first set of non-myopic methods for MOO problems. Prior work on non-myopic BO for single-objective problems relies on the Bellman optimality principle to handle the lookahead reasoning process. However, this principle does not hold for most MOO problems because the reward function needs to satisfy some conditions: scalar variable, monotonicity, and additivity. We address this challenge by using hypervolume improvement (HVI) as our scalarization approach, which allows us to use a lower-bound on the Bellman equation to approximate the finite-horizon using a batch expected hypervolume improvement (EHVI) acquisition function (AF) for MOO. Our formulation naturally allows us to use other improvement-based scalarizations and compare their efficacy to HVI. We derive three non-myopic AFs for MOBO: 1) the Nested AF, which is based on the exact computation of the lower bound, 2) the Joint AF, which is a lower bound on the nested AF, and 3) the BINOM AF, which is a fast and approximate variant based on batch multi-objective acquisition functions. Our experiments on multiple diverse real-world MO problems demonstrate that our non-myopic AFs substantially improve performance over the existing myopic AFs for MOBO.

Active Learning for Derivative-Based Global Sensitivity Analysis with Gaussian Processes

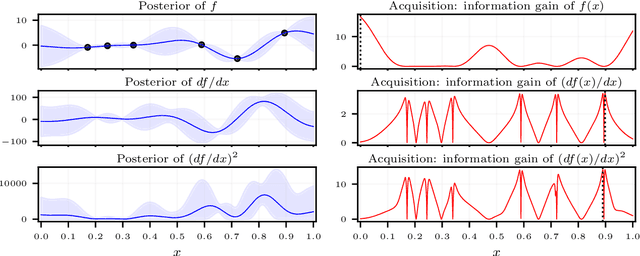
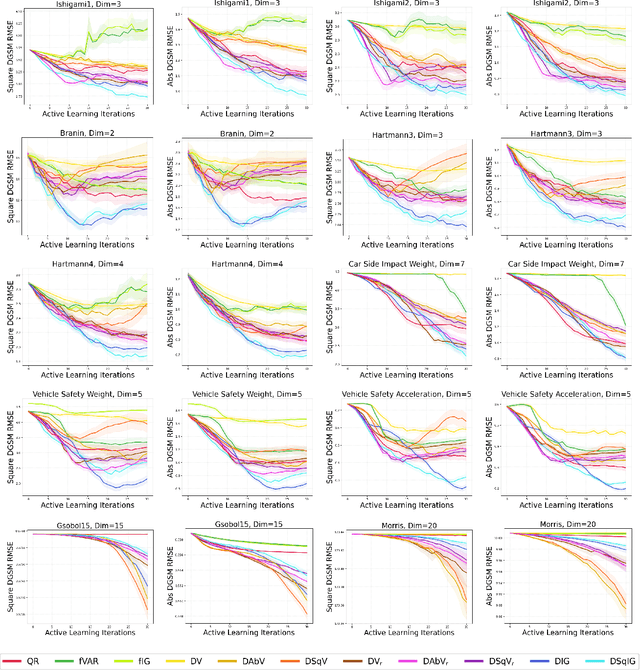
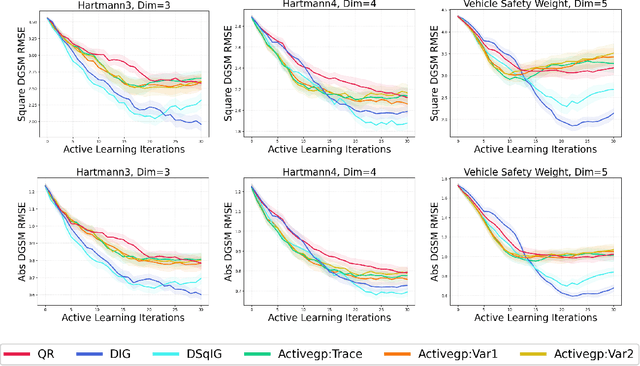
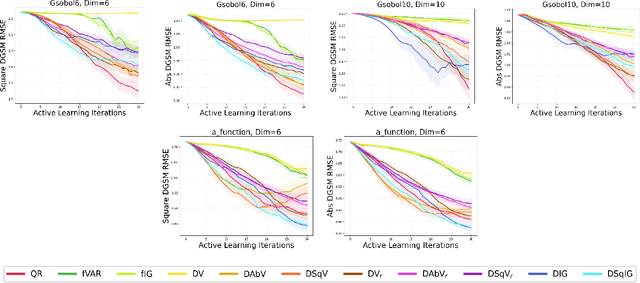
We consider the problem of active learning for global sensitivity analysis of expensive black-box functions. Our aim is to efficiently learn the importance of different input variables, e.g., in vehicle safety experimentation, we study the impact of the thickness of various components on safety objectives. Since function evaluations are expensive, we use active learning to prioritize experimental resources where they yield the most value. We propose novel active learning acquisition functions that directly target key quantities of derivative-based global sensitivity measures (DGSMs) under Gaussian process surrogate models. We showcase the first application of active learning directly to DGSMs, and develop tractable uncertainty reduction and information gain acquisition functions for these measures. Through comprehensive evaluation on synthetic and real-world problems, our study demonstrates how these active learning acquisition strategies substantially enhance the sample efficiency of DGSM estimation, particularly with limited evaluation budgets. Our work paves the way for more efficient and accurate sensitivity analysis in various scientific and engineering applications.

Nested Policy Reinforcement Learning

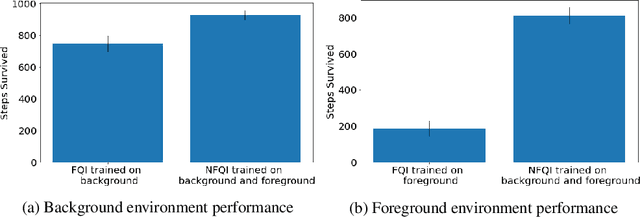
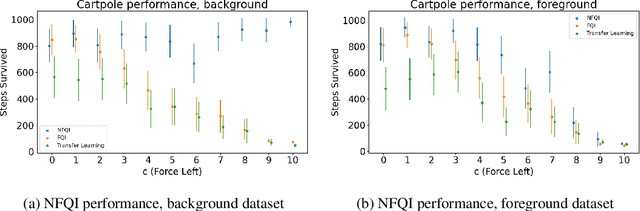
Off-policy reinforcement learning (RL) has proven to be a powerful framework for guiding agents' actions in environments with stochastic rewards and unknown or noisy state dynamics. In many real-world settings, these agents must operate in multiple environments, each with slightly different dynamics. For example, we may be interested in developing policies to guide medical treatment for patients with and without a given disease, or policies to navigate curriculum design for students with and without a learning disability. Here, we introduce nested policy fitted Q-iteration (NFQI), an RL framework that finds optimal policies in environments that exhibit such a structure. Our approach develops a nested $Q$-value function that takes advantage of the shared structure between two groups of observations from two separate environments while allowing their policies to be distinct from one another. We find that NFQI yields policies that rely on relevant features and perform at least as well as a policy that does not consider group structure. We demonstrate NFQI's performance using an OpenAI Gym environment and a clinical decision making RL task. Our results suggest that NFQI can develop policies that are better suited to many real-world clinical environments.

Probabilistic Contrastive Principal Component Analysis

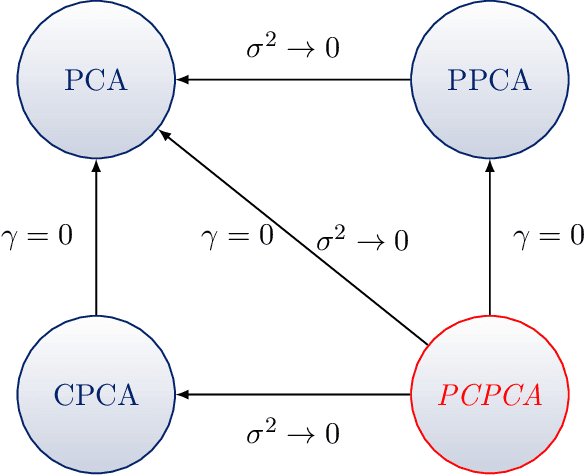
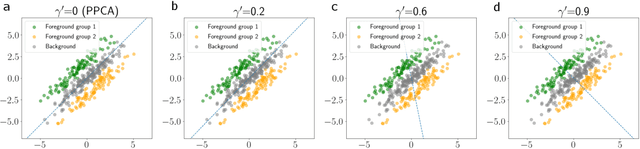
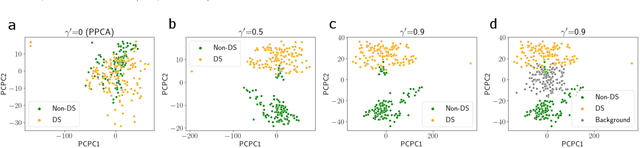
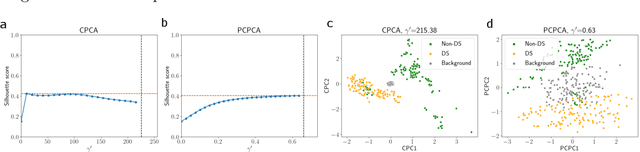
Dimension reduction is useful for exploratory data analysis. In many applications, it is of interest to discover variation that is enriched in a "foreground" dataset relative to a "background" dataset. Recently, contrastive principal component analysis (CPCA) was proposed for this setting. However, the lack of a formal probabilistic model makes it difficult to reason about CPCA and to tune its hyperparameter. In this work, we propose probabilistic contrastive principal component analysis (PCPCA), a model-based alternative to CPCA. We discuss how to set the hyperparameter in theory and in practice, and we show several of PCPCA's advantages, including greater interpretability, uncertainty quantification, robustness to noise and missing data, and the ability to generate data from the model. We demonstrate PCPCA's performance through a series of simulations and experiments with datasets of gene expression, protein expression, and images.

AdaCluster : Adaptive Clustering for Heterogeneous Data

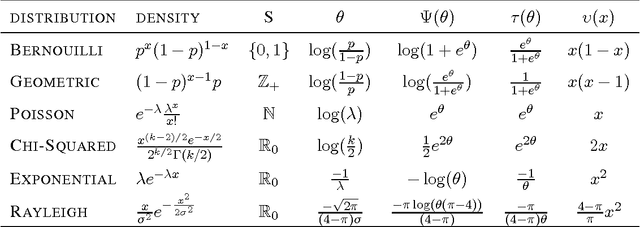
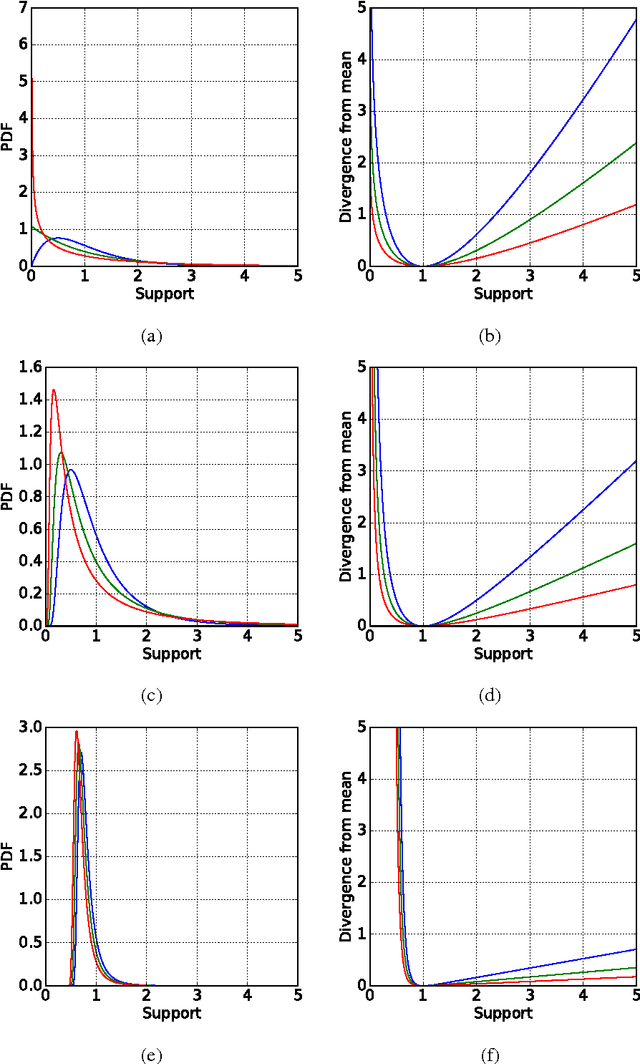
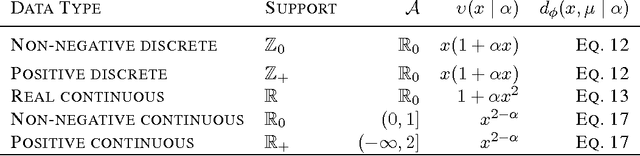
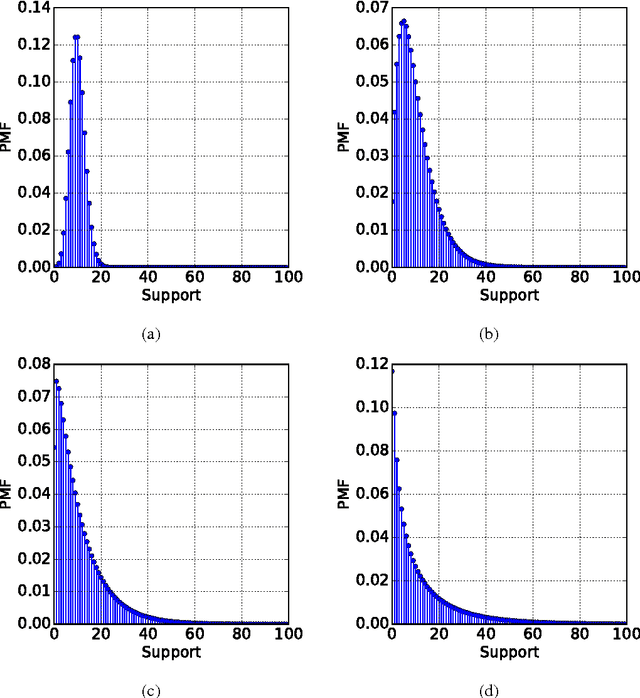
Clustering algorithms start with a fixed divergence, which captures the possibly asymmetric distance between a sample and a centroid. In the mixture model setting, the sample distribution plays the same role. When all attributes have the same topology and dispersion, the data are said to be homogeneous. If the prior knowledge of the distribution is inaccurate or the set of plausible distributions is large, an adaptive approach is essential. The motivation is more compelling for heterogeneous data, where the dispersion or the topology differs among attributes. We propose an adaptive approach to clustering using classes of parametrized Bregman divergences. We first show that the density of a steep exponential dispersion model (EDM) can be represented with a Bregman divergence. We then propose AdaCluster, an expectation-maximization (EM) algorithm to cluster heterogeneous data using classes of steep EDMs. We compare AdaCluster with EM for a Gaussian mixture model on synthetic data and nine UCI data sets. We also propose an adaptive hard clustering algorithm based on Generalized Method of Moments. We compare the hard clustering algorithm with k-means on the UCI data sets. We empirically verified that adaptively learning the underlying topology yields better clustering of heterogeneous data.