AdaCluster : Adaptive Clustering for Heterogeneous Data
Paper and Code
Jan 06, 2017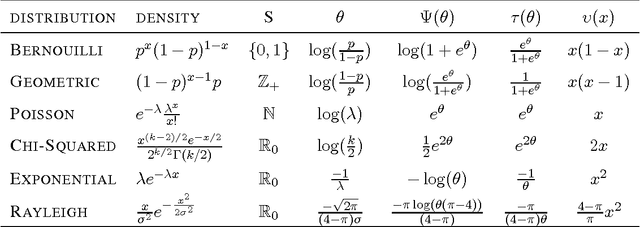
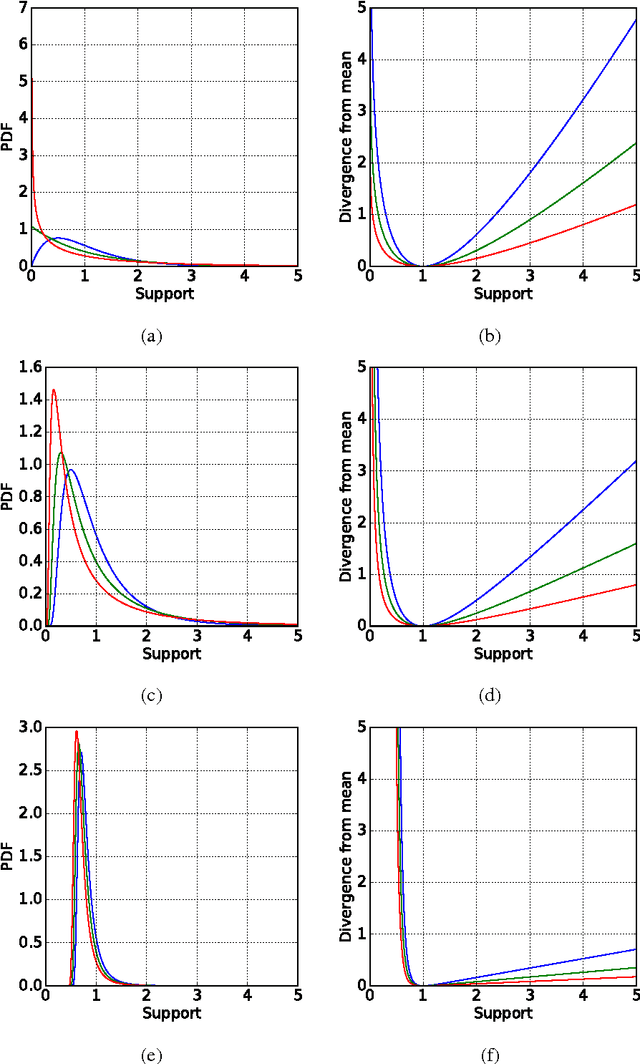
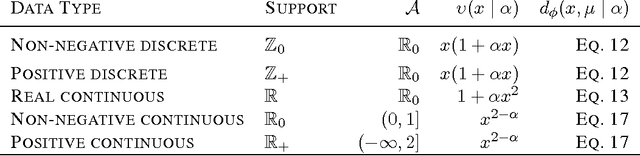
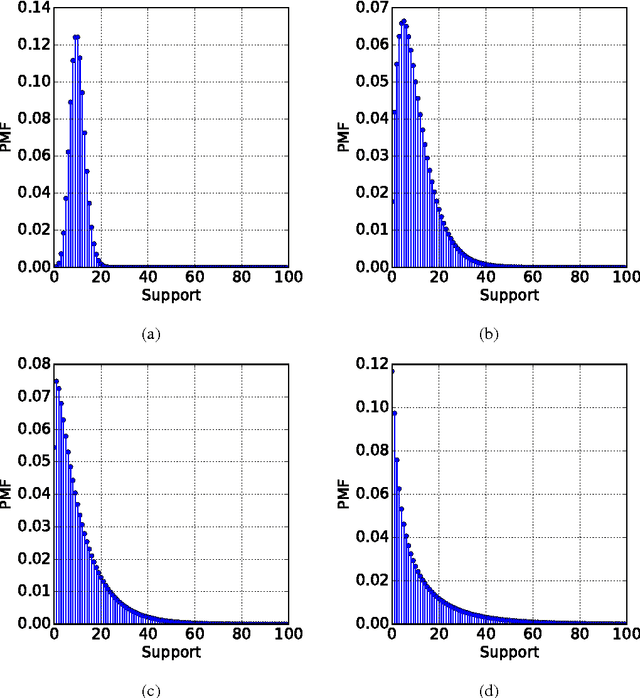
Clustering algorithms start with a fixed divergence, which captures the possibly asymmetric distance between a sample and a centroid. In the mixture model setting, the sample distribution plays the same role. When all attributes have the same topology and dispersion, the data are said to be homogeneous. If the prior knowledge of the distribution is inaccurate or the set of plausible distributions is large, an adaptive approach is essential. The motivation is more compelling for heterogeneous data, where the dispersion or the topology differs among attributes. We propose an adaptive approach to clustering using classes of parametrized Bregman divergences. We first show that the density of a steep exponential dispersion model (EDM) can be represented with a Bregman divergence. We then propose AdaCluster, an expectation-maximization (EM) algorithm to cluster heterogeneous data using classes of steep EDMs. We compare AdaCluster with EM for a Gaussian mixture model on synthetic data and nine UCI data sets. We also propose an adaptive hard clustering algorithm based on Generalized Method of Moments. We compare the hard clustering algorithm with k-means on the UCI data sets. We empirically verified that adaptively learning the underlying topology yields better clustering of heterogeneous data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge