Probabilistic Contrastive Principal Component Analysis
Paper and Code
Dec 14, 2020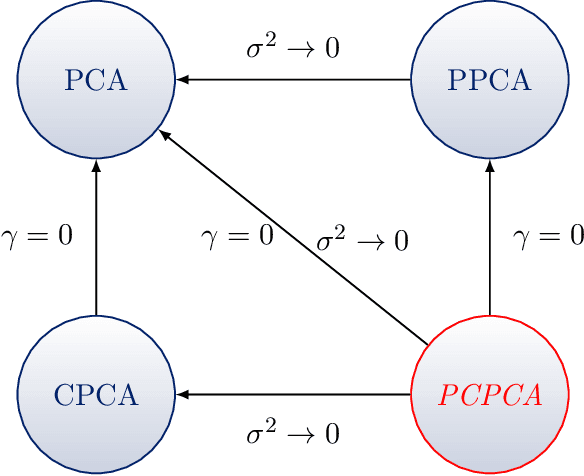
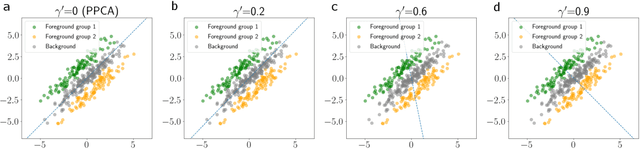
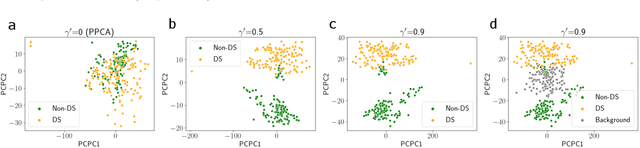
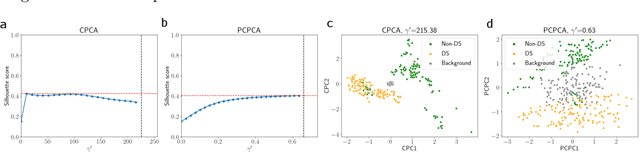
Dimension reduction is useful for exploratory data analysis. In many applications, it is of interest to discover variation that is enriched in a "foreground" dataset relative to a "background" dataset. Recently, contrastive principal component analysis (CPCA) was proposed for this setting. However, the lack of a formal probabilistic model makes it difficult to reason about CPCA and to tune its hyperparameter. In this work, we propose probabilistic contrastive principal component analysis (PCPCA), a model-based alternative to CPCA. We discuss how to set the hyperparameter in theory and in practice, and we show several of PCPCA's advantages, including greater interpretability, uncertainty quantification, robustness to noise and missing data, and the ability to generate data from the model. We demonstrate PCPCA's performance through a series of simulations and experiments with datasets of gene expression, protein expression, and images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge