Non-Myopic Multi-Objective Bayesian Optimization

We consider the problem of finite-horizon sequential experimental design to solve multi-objective optimization (MOO) of expensive black-box objective functions. This problem arises in many real-world applications, including materials design, where we have a small resource budget to make and evaluate candidate materials in the lab. We solve this problem using the framework of Bayesian optimization (BO) and propose the first set of non-myopic methods for MOO problems. Prior work on non-myopic BO for single-objective problems relies on the Bellman optimality principle to handle the lookahead reasoning process. However, this principle does not hold for most MOO problems because the reward function needs to satisfy some conditions: scalar variable, monotonicity, and additivity. We address this challenge by using hypervolume improvement (HVI) as our scalarization approach, which allows us to use a lower-bound on the Bellman equation to approximate the finite-horizon using a batch expected hypervolume improvement (EHVI) acquisition function (AF) for MOO. Our formulation naturally allows us to use other improvement-based scalarizations and compare their efficacy to HVI. We derive three non-myopic AFs for MOBO: 1) the Nested AF, which is based on the exact computation of the lower bound, 2) the Joint AF, which is a lower bound on the nested AF, and 3) the BINOM AF, which is a fast and approximate variant based on batch multi-objective acquisition functions. Our experiments on multiple diverse real-world MO problems demonstrate that our non-myopic AFs substantially improve performance over the existing myopic AFs for MOBO.

Pareto Front-Diverse Batch Multi-Objective Bayesian Optimization

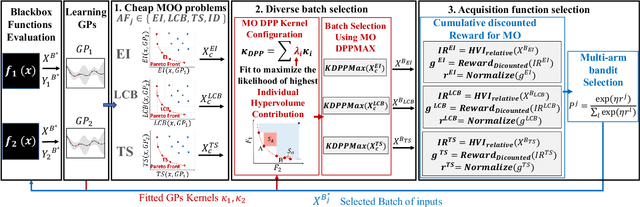
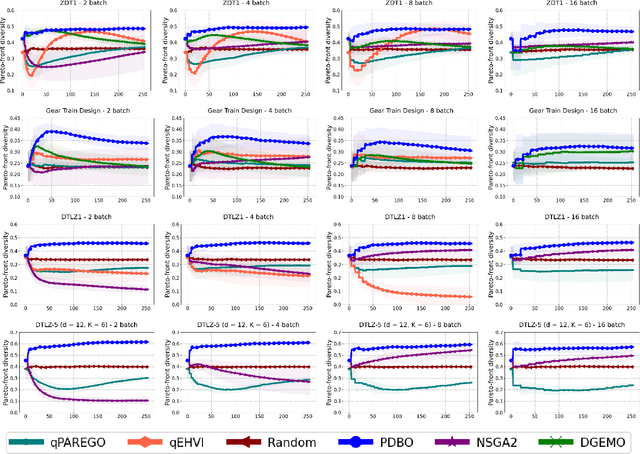
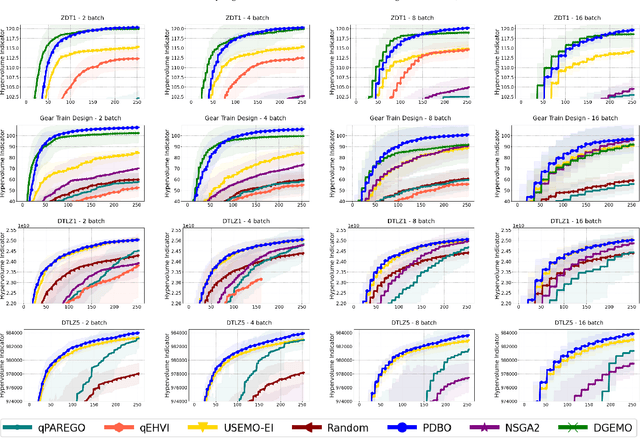
We consider the problem of multi-objective optimization (MOO) of expensive black-box functions with the goal of discovering high-quality and diverse Pareto fronts where we are allowed to evaluate a batch of inputs. This problem arises in many real-world applications including penicillin production where diversity of solutions is critical. We solve this problem in the framework of Bayesian optimization (BO) and propose a novel approach referred to as Pareto front-Diverse Batch Multi-Objective BO (PDBO). PDBO tackles two important challenges: 1) How to automatically select the best acquisition function in each BO iteration, and 2) How to select a diverse batch of inputs by considering multiple objectives. We propose principled solutions to address these two challenges. First, PDBO employs a multi-armed bandit approach to select one acquisition function from a given library. We solve a cheap MOO problem by assigning the selected acquisition function for each expensive objective function to obtain a candidate set of inputs for evaluation. Second, it utilizes Determinantal Point Processes (DPPs) to choose a Pareto-front-diverse batch of inputs for evaluation from the candidate set obtained from the first step. The key parameters for the methods behind these two steps are updated after each round of function evaluations. Experiments on multiple MOO benchmarks demonstrate that PDBO outperforms prior methods in terms of both the quality and diversity of Pareto solutions.

Preference-Aware Constrained Multi-Objective Bayesian Optimization

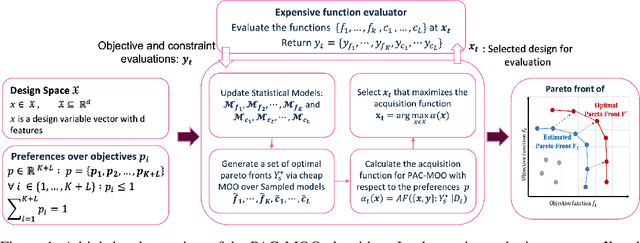
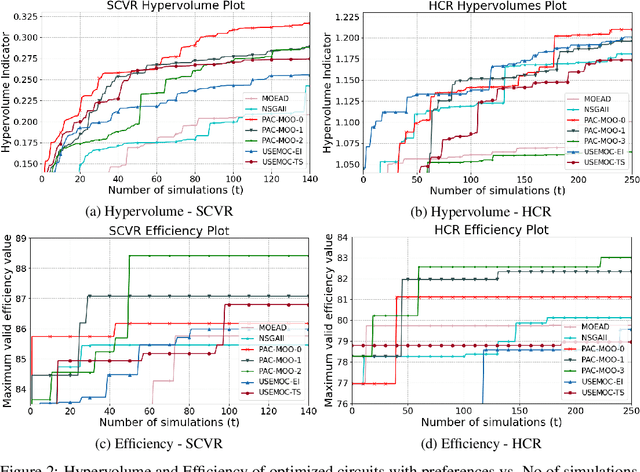
This paper addresses the problem of constrained multi-objective optimization over black-box objective functions with practitioner-specified preferences over the objectives when a large fraction of the input space is infeasible (i.e., violates constraints). This problem arises in many engineering design problems including analog circuits and electric power system design. Our overall goal is to approximate the optimal Pareto set over the small fraction of feasible input designs. The key challenges include the huge size of the design space, multiple objectives and large number of constraints, and the small fraction of feasible input designs which can be identified only after performing expensive simulations. We propose a novel and efficient preference-aware constrained multi-objective Bayesian optimization approach referred to as PAC-MOO to address these challenges. The key idea is to learn surrogate models for both output objectives and constraints, and select the candidate input for evaluation in each iteration that maximizes the information gained about the optimal constrained Pareto front while factoring in the preferences over objectives. Our experiments on two real-world analog circuit design optimization problems demonstrate the efficacy of PAC-MOO over prior methods.