Pareto Front-Diverse Batch Multi-Objective Bayesian Optimization
Paper and Code
Jun 13, 2024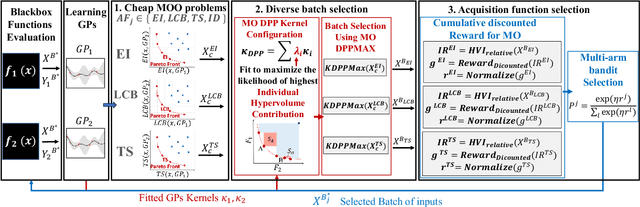
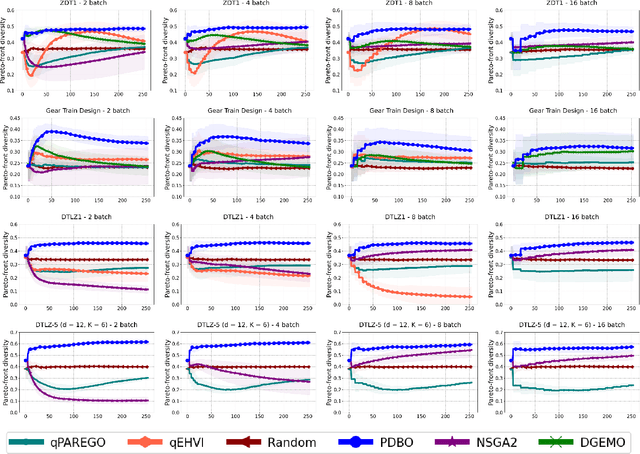
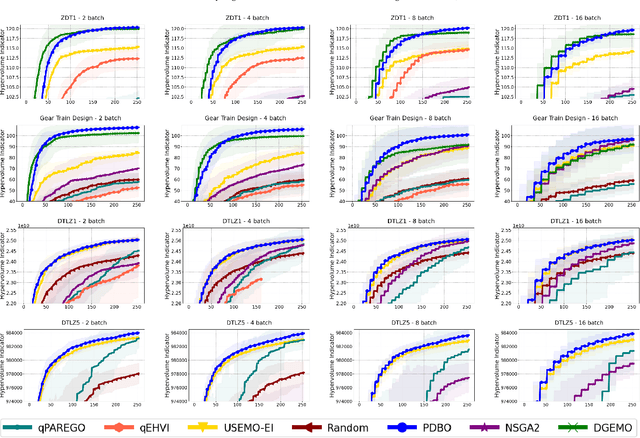
We consider the problem of multi-objective optimization (MOO) of expensive black-box functions with the goal of discovering high-quality and diverse Pareto fronts where we are allowed to evaluate a batch of inputs. This problem arises in many real-world applications including penicillin production where diversity of solutions is critical. We solve this problem in the framework of Bayesian optimization (BO) and propose a novel approach referred to as Pareto front-Diverse Batch Multi-Objective BO (PDBO). PDBO tackles two important challenges: 1) How to automatically select the best acquisition function in each BO iteration, and 2) How to select a diverse batch of inputs by considering multiple objectives. We propose principled solutions to address these two challenges. First, PDBO employs a multi-armed bandit approach to select one acquisition function from a given library. We solve a cheap MOO problem by assigning the selected acquisition function for each expensive objective function to obtain a candidate set of inputs for evaluation. Second, it utilizes Determinantal Point Processes (DPPs) to choose a Pareto-front-diverse batch of inputs for evaluation from the candidate set obtained from the first step. The key parameters for the methods behind these two steps are updated after each round of function evaluations. Experiments on multiple MOO benchmarks demonstrate that PDBO outperforms prior methods in terms of both the quality and diversity of Pareto solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge