Causal Bayesian Optimization with Unknown Graphs

Causal Bayesian Optimization (CBO) is a methodology designed to optimize an outcome variable by leveraging known causal relationships through targeted interventions. Traditional CBO methods require a fully and accurately specified causal graph, which is a limitation in many real-world scenarios where such graphs are unknown. To address this, we propose a new method for the CBO framework that operates without prior knowledge of the causal graph. Consistent with causal bandit theory, we demonstrate through theoretical analysis and that focusing on the direct causal parents of the target variable is sufficient for optimization, and provide empirical validation in the context of CBO. Furthermore we introduce a new method that learns a Bayesian posterior over the direct parents of the target variable. This allows us to optimize the outcome variable while simultaneously learning the causal structure. Our contributions include a derivation of the closed-form posterior distribution for the linear case. In the nonlinear case where the posterior is not tractable, we present a Gaussian Process (GP) approximation that still enables CBO by inferring the parents of the outcome variable. The proposed method performs competitively with existing benchmarks and scales well to larger graphs, making it a practical tool for real-world applications where causal information is incomplete.

Preference-Guided Diffusion for Multi-Objective Offline Optimization

Offline multi-objective optimization aims to identify Pareto-optimal solutions given a dataset of designs and their objective values. In this work, we propose a preference-guided diffusion model that generates Pareto-optimal designs by leveraging a classifier-based guidance mechanism. Our guidance classifier is a preference model trained to predict the probability that one design dominates another, directing the diffusion model toward optimal regions of the design space. Crucially, this preference model generalizes beyond the training distribution, enabling the discovery of Pareto-optimal solutions outside the observed dataset. We introduce a novel diversity-aware preference guidance, augmenting Pareto dominance preference with diversity criteria. This ensures that generated solutions are optimal and well-distributed across the objective space, a capability absent in prior generative methods for offline multi-objective optimization. We evaluate our approach on various continuous offline multi-objective optimization tasks and find that it consistently outperforms other inverse/generative approaches while remaining competitive with forward/surrogate-based optimization methods. Our results highlight the effectiveness of classifier-guided diffusion models in generating diverse and high-quality solutions that approximate the Pareto front well.

Challenges and Considerations in the Evaluation of Bayesian Causal Discovery

Representing uncertainty in causal discovery is a crucial component for experimental design, and more broadly, for safe and reliable causal decision making. Bayesian Causal Discovery (BCD) offers a principled approach to encapsulating this uncertainty. Unlike non-Bayesian causal discovery, which relies on a single estimated causal graph and model parameters for assessment, evaluating BCD presents challenges due to the nature of its inferred quantity - the posterior distribution. As a result, the research community has proposed various metrics to assess the quality of the approximate posterior. However, there is, to date, no consensus on the most suitable metric(s) for evaluation. In this work, we reexamine this question by dissecting various metrics and understanding their limitations. Through extensive empirical evaluation, we find that many existing metrics fail to exhibit a strong correlation with the quality of approximation to the true posterior, especially in scenarios with low sample sizes where BCD is most desirable. We highlight the suitability (or lack thereof) of these metrics under two distinct factors: the identifiability of the underlying causal model and the quantity of available data. Both factors affect the entropy of the true posterior, indicating that the current metrics are less fitting in settings of higher entropy. Our findings underline the importance of a more nuanced evaluation of new methods by taking into account the nature of the true posterior, as well as guide and motivate the development of new evaluation procedures for this challenge.

Amortized Active Causal Induction with Deep Reinforcement Learning

We present Causal Amortized Active Structure Learning (CAASL), an active intervention design policy that can select interventions that are adaptive, real-time and that does not require access to the likelihood. This policy, an amortized network based on the transformer, is trained with reinforcement learning on a simulator of the design environment, and a reward function that measures how close the true causal graph is to a causal graph posterior inferred from the gathered data. On synthetic data and a single-cell gene expression simulator, we demonstrate empirically that the data acquired through our policy results in a better estimate of the underlying causal graph than alternative strategies. Our design policy successfully achieves amortized intervention design on the distribution of the training environment while also generalizing well to distribution shifts in test-time design environments. Further, our policy also demonstrates excellent zero-shot generalization to design environments with dimensionality higher than that during training, and to intervention types that it has not been trained on.

BayesDAG: Gradient-Based Posterior Sampling for Causal Discovery

Bayesian causal discovery aims to infer the posterior distribution over causal models from observed data, quantifying epistemic uncertainty and benefiting downstream tasks. However, computational challenges arise due to joint inference over combinatorial space of Directed Acyclic Graphs (DAGs) and nonlinear functions. Despite recent progress towards efficient posterior inference over DAGs, existing methods are either limited to variational inference on node permutation matrices for linear causal models, leading to compromised inference accuracy, or continuous relaxation of adjacency matrices constrained by a DAG regularizer, which cannot ensure resulting graphs are DAGs. In this work, we introduce a scalable Bayesian causal discovery framework based on stochastic gradient Markov Chain Monte Carlo (SG-MCMC) that overcomes these limitations. Our approach directly samples DAGs from the posterior without requiring any DAG regularization, simultaneously draws function parameter samples and is applicable to both linear and nonlinear causal models. To enable our approach, we derive a novel equivalence to the permutation-based DAG learning, which opens up possibilities of using any relaxed gradient estimator defined over permutations. To our knowledge, this is the first framework applying gradient-based MCMC sampling for causal discovery. Empirical evaluations on synthetic and real-world datasets demonstrate our approach's effectiveness compared to state-of-the-art baselines.

Differentiable Multi-Target Causal Bayesian Experimental Design

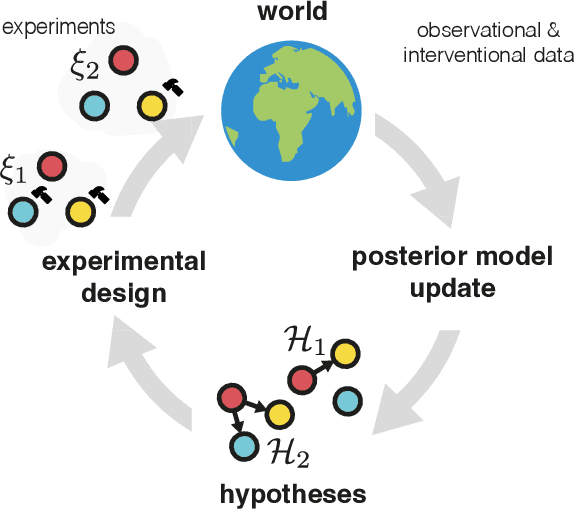
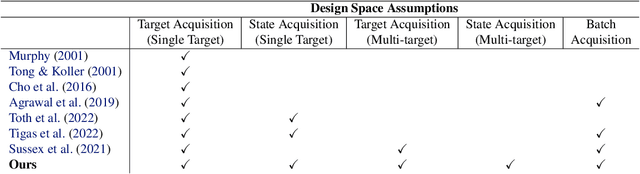
We introduce a gradient-based approach for the problem of Bayesian optimal experimental design to learn causal models in a batch setting -- a critical component for causal discovery from finite data where interventions can be costly or risky. Existing methods rely on greedy approximations to construct a batch of experiments while using black-box methods to optimize over a single target-state pair to intervene with. In this work, we completely dispose of the black-box optimization techniques and greedy heuristics and instead propose a conceptually simple end-to-end gradient-based optimization procedure to acquire a set of optimal intervention target-state pairs. Such a procedure enables parameterization of the design space to efficiently optimize over a batch of multi-target-state interventions, a setting which has hitherto not been explored due to its complexity. We demonstrate that our proposed method outperforms baselines and existing acquisition strategies in both single-target and multi-target settings across a number of synthetic datasets.

Trust Your $ abla$: Gradient-based Intervention Targeting for Causal Discovery

Inferring causal structure from data is a challenging task of fundamental importance in science. Observational data are often insufficient to identify a system's causal structure uniquely. While conducting interventions (i.e., experiments) can improve the identifiability, such samples are usually challenging and expensive to obtain. Hence, experimental design approaches for causal discovery aim to minimize the number of interventions by estimating the most informative intervention target. In this work, we propose a novel Gradient-based Intervention Targeting method, abbreviated GIT, that 'trusts' the gradient estimator of a gradient-based causal discovery framework to provide signals for the intervention acquisition function. We provide extensive experiments in simulated and real-world datasets and demonstrate that GIT performs on par with competitive baselines, surpassing them in the low-data regime.

Learning Latent Structural Causal Models

Causal learning has long concerned itself with the accurate recovery of underlying causal mechanisms. Such causal modelling enables better explanations of out-of-distribution data. Prior works on causal learning assume that the high-level causal variables are given. However, in machine learning tasks, one often operates on low-level data like image pixels or high-dimensional vectors. In such settings, the entire Structural Causal Model (SCM) -- structure, parameters, \textit{and} high-level causal variables -- is unobserved and needs to be learnt from low-level data. We treat this problem as Bayesian inference of the latent SCM, given low-level data. For linear Gaussian additive noise SCMs, we present a tractable approximate inference method which performs joint inference over the causal variables, structure and parameters of the latent SCM from random, known interventions. Experiments are performed on synthetic datasets and a causally generated image dataset to demonstrate the efficacy of our approach. We also perform image generation from unseen interventions, thereby verifying out of distribution generalization for the proposed causal model.

Latent Variable Models for Bayesian Causal Discovery

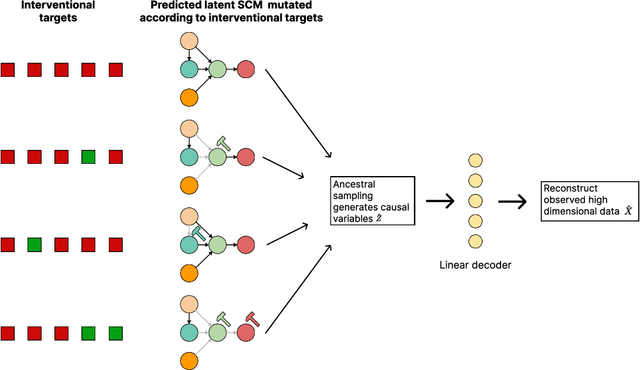
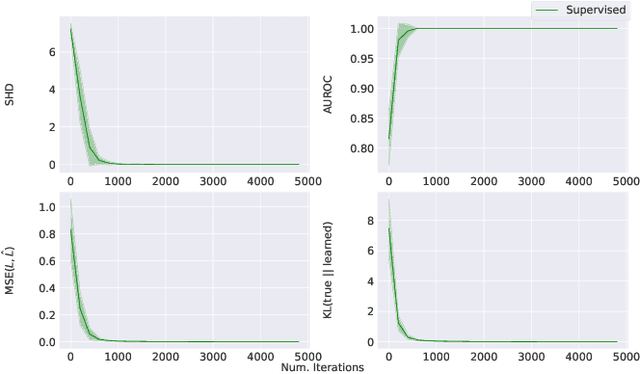
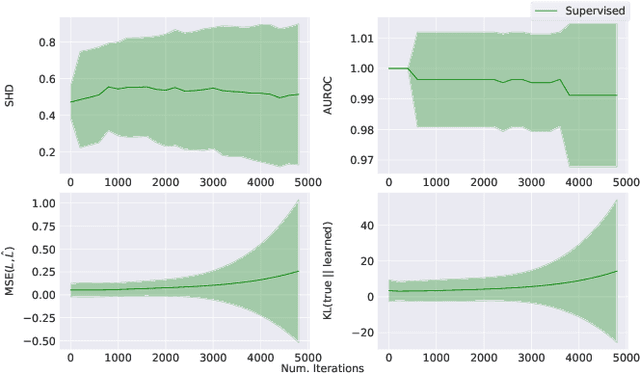
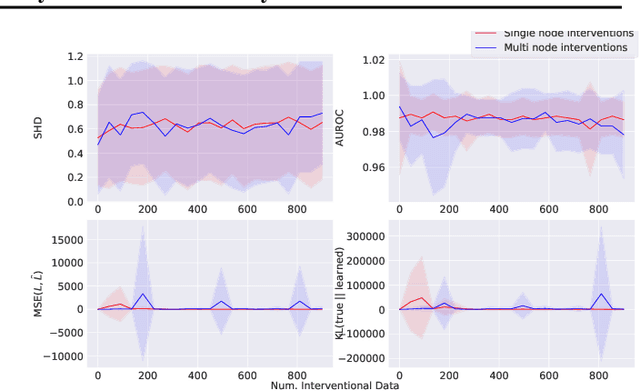
Learning predictors that do not rely on spurious correlations involves building causal representations. However, learning such a representation is very challenging. We, therefore, formulate the problem of learning a causal representation from high dimensional data and study causal recovery with synthetic data. This work introduces a latent variable decoder model, Decoder BCD, for Bayesian causal discovery and performs experiments in mildly supervised and unsupervised settings. We present a series of synthetic experiments to characterize important factors for causal discovery and show that using known intervention targets as labels helps in unsupervised Bayesian inference over structure and parameters of linear Gaussian additive noise latent structural causal models.

Interventions, Where and How? Experimental Design for Causal Models at Scale

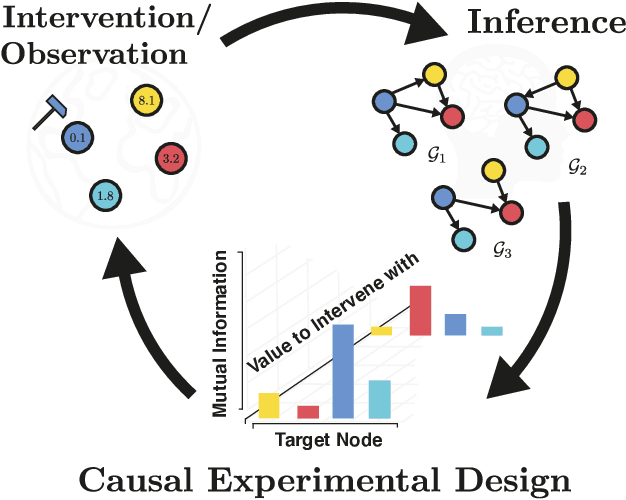
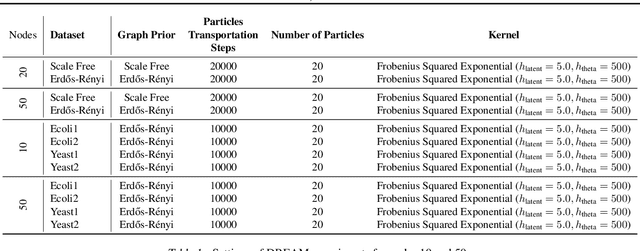
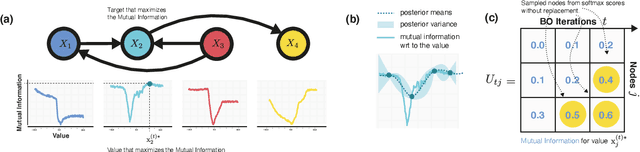
Causal discovery from observational and interventional data is challenging due to limited data and non-identifiability which introduces uncertainties in estimating the underlying structural causal model (SCM). Incorporating these uncertainties and selecting optimal experiments (interventions) to perform can help to identify the true SCM faster. Existing methods in experimental design for causal discovery from limited data either rely on linear assumptions for the SCM or select only the intervention target. In this paper, we incorporate recent advances in Bayesian causal discovery into the Bayesian optimal experimental design framework, which allows for active causal discovery of nonlinear, large SCMs, while selecting both the target and the value to intervene with. We demonstrate the performance of the proposed method on synthetic graphs (Erdos-R\`enyi, Scale Free) for both linear and nonlinear SCMs as well as on the in-silico single-cell gene regulatory network dataset, DREAM.