Large Language Models for Zero-shot Inference of Causal Structures in Biology

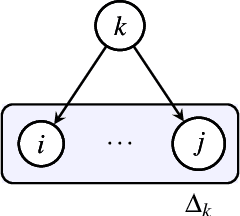
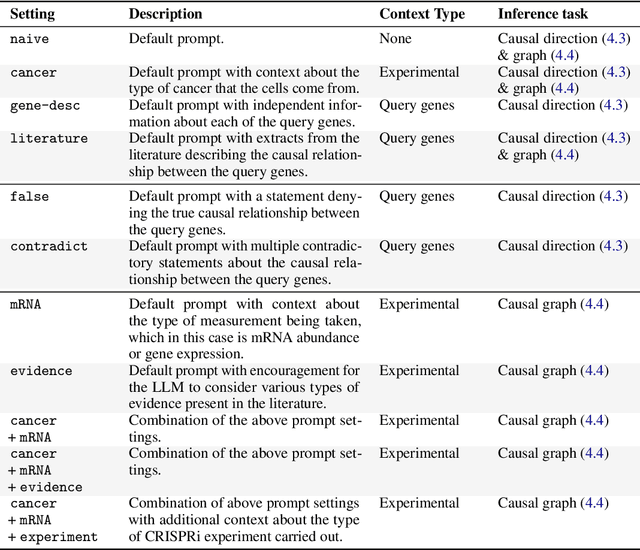
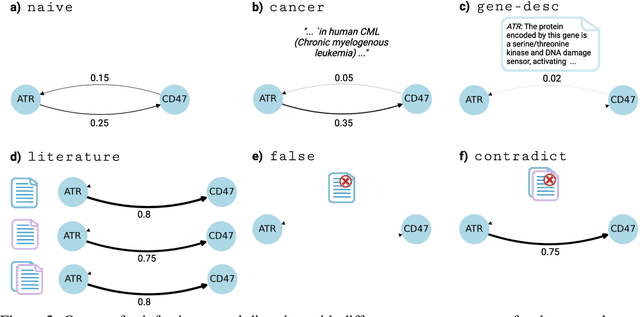
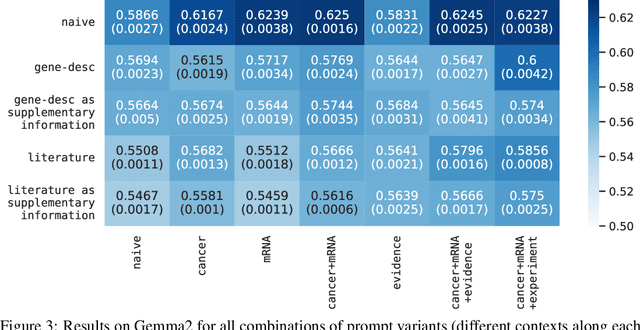
Genes, proteins and other biological entities influence one another via causal molecular networks. Causal relationships in such networks are mediated by complex and diverse mechanisms, through latent variables, and are often specific to cellular context. It remains challenging to characterise such networks in practice. Here, we present a novel framework to evaluate large language models (LLMs) for zero-shot inference of causal relationships in biology. In particular, we systematically evaluate causal claims obtained from an LLM using real-world interventional data. This is done over one hundred variables and thousands of causal hypotheses. Furthermore, we consider several prompting and retrieval-augmentation strategies, including large, and potentially conflicting, collections of scientific articles. Our results show that with tailored augmentation and prompting, even relatively small LLMs can capture meaningful aspects of causal structure in biological systems. This supports the notion that LLMs could act as orchestration tools in biological discovery, by helping to distil current knowledge in ways amenable to downstream analysis. Our approach to assessing LLMs with respect to experimental data is relevant for a broad range of problems at the intersection of causal learning, LLMs and scientific discovery.

Can foundation models actively gather information in interactive environments to test hypotheses?

While problem solving is a standard evaluation task for foundation models, a crucial component of problem solving -- actively and strategically gathering information to test hypotheses -- has not been closely investigated. To assess the information gathering abilities of foundation models in interactive environments, we introduce a framework in which a model must determine the factors influencing a hidden reward function by iteratively reasoning about its previously gathered information and proposing its next exploratory action to maximize information gain at each step. We implement this framework in both a text-based environment, which offers a tightly controlled setting and enables high-throughput parameter sweeps, and in an embodied 3D environment, which requires addressing complexities of multi-modal interaction more relevant to real-world applications. We further investigate whether approaches such as self-correction and increased inference time improve information gathering efficiency. In a relatively simple task that requires identifying a single rewarding feature, we find that LLM's information gathering capability is close to optimal. However, when the model must identify a conjunction of rewarding features, performance is suboptimal. The hit in performance is due partly to the model translating task description to a policy and partly to the model's effectiveness in using its in-context memory. Performance is comparable in both text and 3D embodied environments, although imperfect visual object recognition reduces its accuracy in drawing conclusions from gathered information in the 3D embodied case. For single-feature-based rewards, we find that smaller models curiously perform better; for conjunction-based rewards, incorporating self correction into the model improves performance.

AI-Assisted Generation of Difficult Math Questions

Current LLM training positions mathematical reasoning as a core capability. With publicly available sources fully tapped, there is unmet demand for diverse and challenging math questions. Relying solely on human experts is both time-consuming and costly, while LLM-generated questions often lack the requisite diversity and difficulty. We present a design framework that combines the strengths of LLMs with a human-in-the-loop approach to generate a diverse array of challenging math questions. We leverage LLM metacognition skills [Didolkar et al., 2024] of a strong LLM to extract core "skills" from existing math datasets. These skills serve as the basis for generating novel and difficult questions by prompting the LLM with random pairs of core skills. The use of two different skills within each question makes finding such questions an "out of distribution" task for both LLMs and humans. Our pipeline employs LLMs to iteratively generate and refine questions and solutions through multiturn prompting. Human annotators then verify and further refine the questions, with their efficiency enhanced via further LLM interactions. Applying this pipeline on skills extracted from the MATH dataset [Hendrycks et al., 2021] resulted in MATH$^2$ - a dataset of higher-quality math questions, as evidenced by: (a) Lower performance of all models on MATH$^2$ than on MATH (b) Higher performance on MATH when using MATH$^2$ questions as in-context examples. Although focused on mathematics, our methodology seems applicable to other domains requiring structured reasoning, and potentially as a component of scalable oversight. Also of interest is a striking relationship observed between models' performance on the new dataset: the success rate on MATH$^2$ is the square on MATH, suggesting that successfully solving the question in MATH$^2$ requires a nontrivial combination of two distinct math skills.

Learning Beyond Pattern Matching? Assaying Mathematical Understanding in LLMs

We are beginning to see progress in language model assisted scientific discovery. Motivated by the use of LLMs as a general scientific assistant, this paper assesses the domain knowledge of LLMs through its understanding of different mathematical skills required to solve problems. In particular, we look at not just what the pre-trained model already knows, but how it learned to learn from information during in-context learning or instruction-tuning through exploiting the complex knowledge structure within mathematics. Motivated by the Neural Tangent Kernel (NTK), we propose \textit{NTKEval} to assess changes in LLM's probability distribution via training on different kinds of math data. Our systematic analysis finds evidence of domain understanding during in-context learning. By contrast, certain instruction-tuning leads to similar performance changes irrespective of training on different data, suggesting a lack of domain understanding across different skills.

Metacognitive Capabilities of LLMs: An Exploration in Mathematical Problem Solving

Metacognitive knowledge refers to humans' intuitive knowledge of their own thinking and reasoning processes. Today's best LLMs clearly possess some reasoning processes. The paper gives evidence that they also have metacognitive knowledge, including ability to name skills and procedures to apply given a task. We explore this primarily in context of math reasoning, developing a prompt-guided interaction procedure to get a powerful LLM to assign sensible skill labels to math questions, followed by having it perform semantic clustering to obtain coarser families of skill labels. These coarse skill labels look interpretable to humans. To validate that these skill labels are meaningful and relevant to the LLM's reasoning processes we perform the following experiments. (a) We ask GPT-4 to assign skill labels to training questions in math datasets GSM8K and MATH. (b) When using an LLM to solve the test questions, we present it with the full list of skill labels and ask it to identify the skill needed. Then it is presented with randomly selected exemplar solved questions associated with that skill label. This improves accuracy on GSM8k and MATH for several strong LLMs, including code-assisted models. The methodology presented is domain-agnostic, even though this article applies it to math problems.

DiscoGen: Learning to Discover Gene Regulatory Networks

Accurately inferring Gene Regulatory Networks (GRNs) is a critical and challenging task in biology. GRNs model the activatory and inhibitory interactions between genes and are inherently causal in nature. To accurately identify GRNs, perturbational data is required. However, most GRN discovery methods only operate on observational data. Recent advances in neural network-based causal discovery methods have significantly improved causal discovery, including handling interventional data, improvements in performance and scalability. However, applying state-of-the-art (SOTA) causal discovery methods in biology poses challenges, such as noisy data and a large number of samples. Thus, adapting the causal discovery methods is necessary to handle these challenges. In this paper, we introduce DiscoGen, a neural network-based GRN discovery method that can denoise gene expression measurements and handle interventional data. We demonstrate that our model outperforms SOTA neural network-based causal discovery methods.

Learning How to Infer Partial MDPs for In-Context Adaptation and Exploration

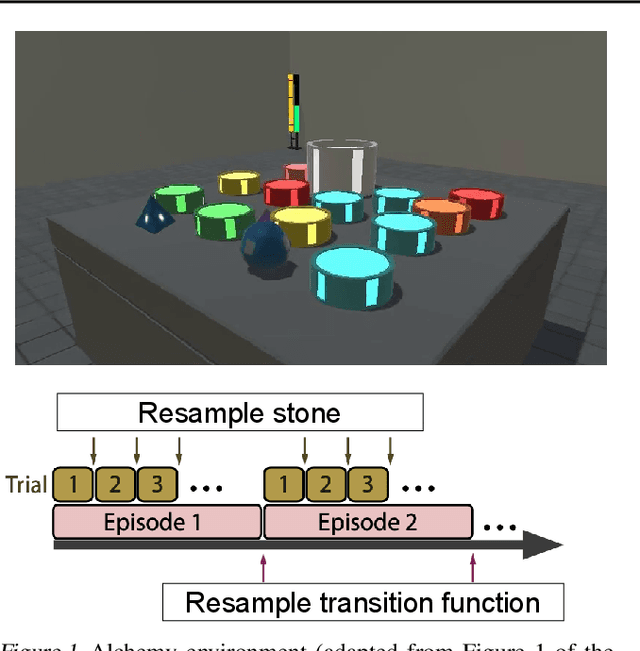
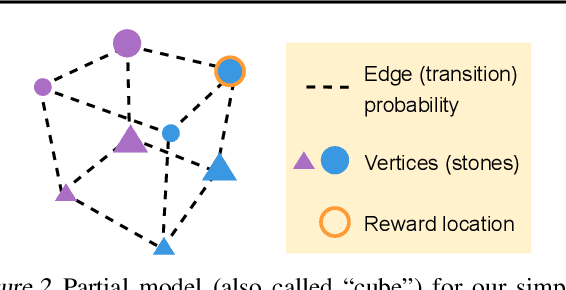
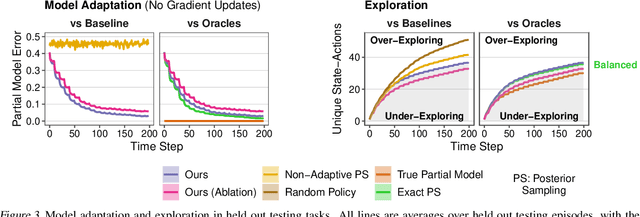
To generalize across tasks, an agent should acquire knowledge from past tasks that facilitate adaptation and exploration in future tasks. We focus on the problem of in-context adaptation and exploration, where an agent only relies on context, i.e., history of states, actions and/or rewards, rather than gradient-based updates. Posterior sampling (extension of Thompson sampling) is a promising approach, but it requires Bayesian inference and dynamic programming, which often involve unknowns (e.g., a prior) and costly computations. To address these difficulties, we use a transformer to learn an inference process from training tasks and consider a hypothesis space of partial models, represented as small Markov decision processes that are cheap for dynamic programming. In our version of the Symbolic Alchemy benchmark, our method's adaptation speed and exploration-exploitation balance approach those of an exact posterior sampling oracle. We also show that even though partial models exclude relevant information from the environment, they can nevertheless lead to good policies.

Learning Latent Structural Causal Models

Causal learning has long concerned itself with the accurate recovery of underlying causal mechanisms. Such causal modelling enables better explanations of out-of-distribution data. Prior works on causal learning assume that the high-level causal variables are given. However, in machine learning tasks, one often operates on low-level data like image pixels or high-dimensional vectors. In such settings, the entire Structural Causal Model (SCM) -- structure, parameters, \textit{and} high-level causal variables -- is unobserved and needs to be learnt from low-level data. We treat this problem as Bayesian inference of the latent SCM, given low-level data. For linear Gaussian additive noise SCMs, we present a tractable approximate inference method which performs joint inference over the causal variables, structure and parameters of the latent SCM from random, known interventions. Experiments are performed on synthetic datasets and a causally generated image dataset to demonstrate the efficacy of our approach. We also perform image generation from unseen interventions, thereby verifying out of distribution generalization for the proposed causal model.

Towards Understanding How Machines Can Learn Causal Overhypotheses

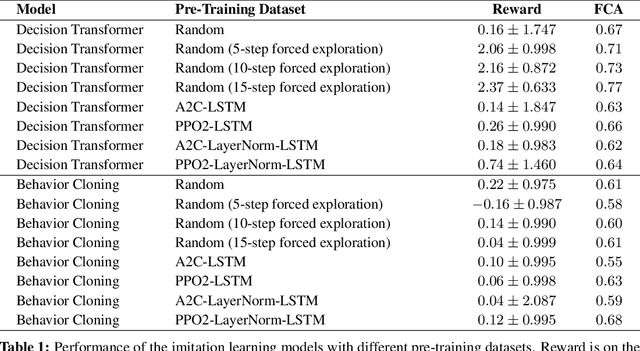
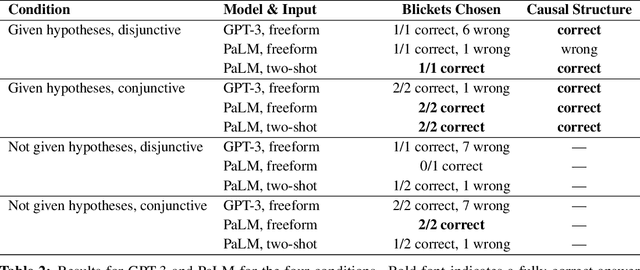
Recent work in machine learning and cognitive science has suggested that understanding causal information is essential to the development of intelligence. The extensive literature in cognitive science using the ``blicket detector'' environment shows that children are adept at many kinds of causal inference and learning. We propose to adapt that environment for machine learning agents. One of the key challenges for current machine learning algorithms is modeling and understanding causal overhypotheses: transferable abstract hypotheses about sets of causal relationships. In contrast, even young children spontaneously learn and use causal overhypotheses. In this work, we present a new benchmark -- a flexible environment which allows for the evaluation of existing techniques under variable causal overhypotheses -- and demonstrate that many existing state-of-the-art methods have trouble generalizing in this environment. The code and resources for this benchmark are available at https://github.com/CannyLab/casual_overhypotheses.

On the Generalization and Adaption Performance of Causal Models

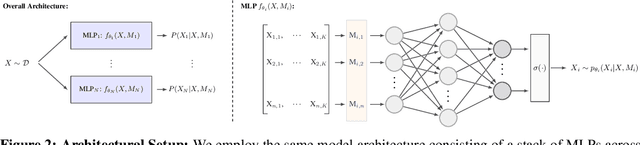
Learning models that offer robust out-of-distribution generalization and fast adaptation is a key challenge in modern machine learning. Modelling causal structure into neural networks holds the promise to accomplish robust zero and few-shot adaptation. Recent advances in differentiable causal discovery have proposed to factorize the data generating process into a set of modules, i.e. one module for the conditional distribution of every variable where only causal parents are used as predictors. Such a modular decomposition of knowledge enables adaptation to distributions shifts by only updating a subset of parameters. In this work, we systematically study the generalization and adaption performance of such modular neural causal models by comparing it to monolithic models and structured models where the set of predictors is not constrained to causal parents. Our analysis shows that the modular neural causal models outperform other models on both zero and few-shot adaptation in low data regimes and offer robust generalization. We also found that the effects are more significant for sparser graphs as compared to denser graphs.