On the Generalization and Adaption Performance of Causal Models
Paper and Code
Jun 09, 2022

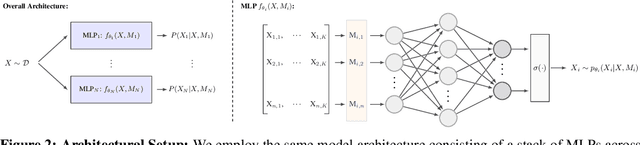

Learning models that offer robust out-of-distribution generalization and fast adaptation is a key challenge in modern machine learning. Modelling causal structure into neural networks holds the promise to accomplish robust zero and few-shot adaptation. Recent advances in differentiable causal discovery have proposed to factorize the data generating process into a set of modules, i.e. one module for the conditional distribution of every variable where only causal parents are used as predictors. Such a modular decomposition of knowledge enables adaptation to distributions shifts by only updating a subset of parameters. In this work, we systematically study the generalization and adaption performance of such modular neural causal models by comparing it to monolithic models and structured models where the set of predictors is not constrained to causal parents. Our analysis shows that the modular neural causal models outperform other models on both zero and few-shot adaptation in low data regimes and offer robust generalization. We also found that the effects are more significant for sparser graphs as compared to denser graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge