Large Language Models for Zero-shot Inference of Causal Structures in Biology

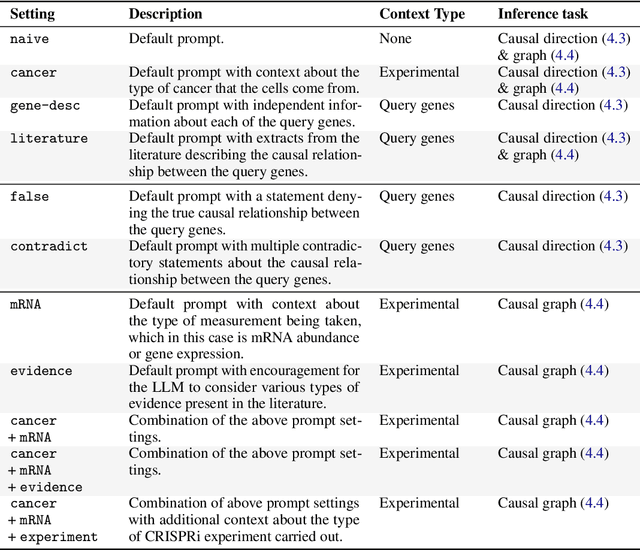
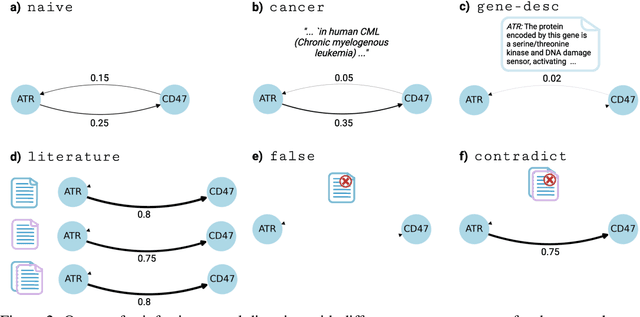
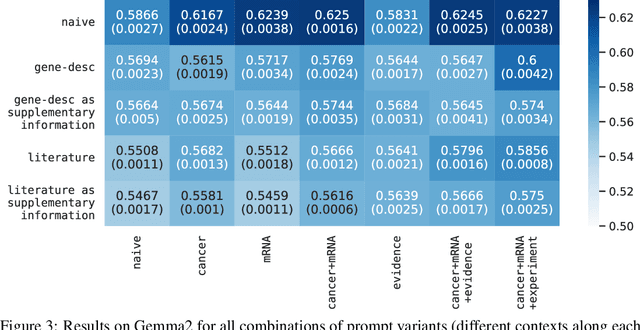
Genes, proteins and other biological entities influence one another via causal molecular networks. Causal relationships in such networks are mediated by complex and diverse mechanisms, through latent variables, and are often specific to cellular context. It remains challenging to characterise such networks in practice. Here, we present a novel framework to evaluate large language models (LLMs) for zero-shot inference of causal relationships in biology. In particular, we systematically evaluate causal claims obtained from an LLM using real-world interventional data. This is done over one hundred variables and thousands of causal hypotheses. Furthermore, we consider several prompting and retrieval-augmentation strategies, including large, and potentially conflicting, collections of scientific articles. Our results show that with tailored augmentation and prompting, even relatively small LLMs can capture meaningful aspects of causal structure in biological systems. This supports the notion that LLMs could act as orchestration tools in biological discovery, by helping to distil current knowledge in ways amenable to downstream analysis. Our approach to assessing LLMs with respect to experimental data is relevant for a broad range of problems at the intersection of causal learning, LLMs and scientific discovery.

Simulation-based Benchmarking for Causal Structure Learning in Gene Perturbation Experiments

Causal structure learning (CSL) refers to the task of learning causal relationships from data. Advances in CSL now allow learning of causal graphs in diverse application domains, which has the potential to facilitate data-driven causal decision-making. Real-world CSL performance depends on a number of $\textit{context-specific}$ factors, including context-specific data distributions and non-linear dependencies, that are important in practical use-cases. However, our understanding of how to assess and select CSL methods in specific contexts remains limited. To address this gap, we present $\textit{CausalRegNet}$, a multiplicative effect structural causal model that allows for generating observational and interventional data incorporating context-specific properties, with a focus on the setting of gene perturbation experiments. Using real-world gene perturbation data, we show that CausalRegNet generates accurate distributions and scales far better than current simulation frameworks. We illustrate the use of CausalRegNet in assessing CSL methods in the context of interventional experiments in biology.

Learning Latent Dynamics via Invariant Decomposition and (Spatio-)Temporal Transformers

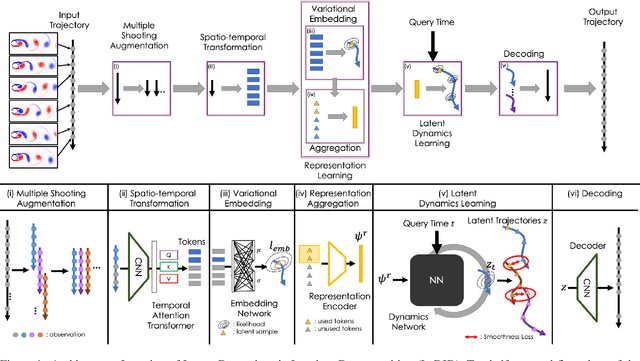
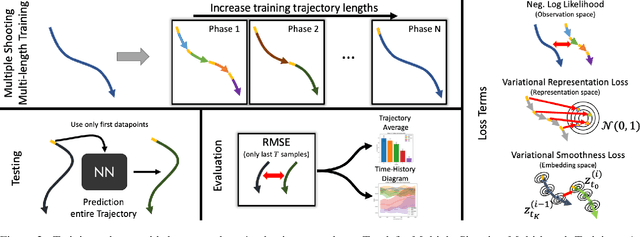
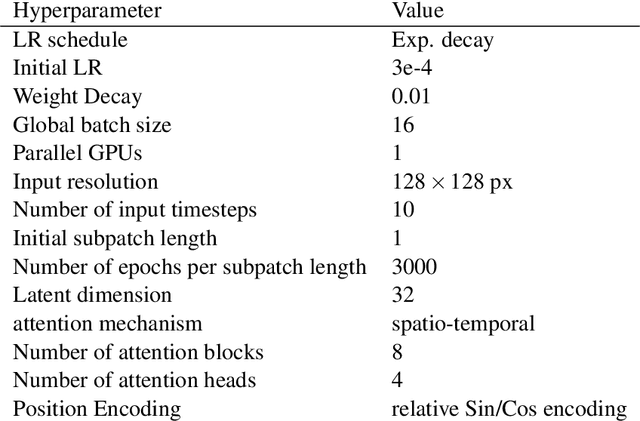
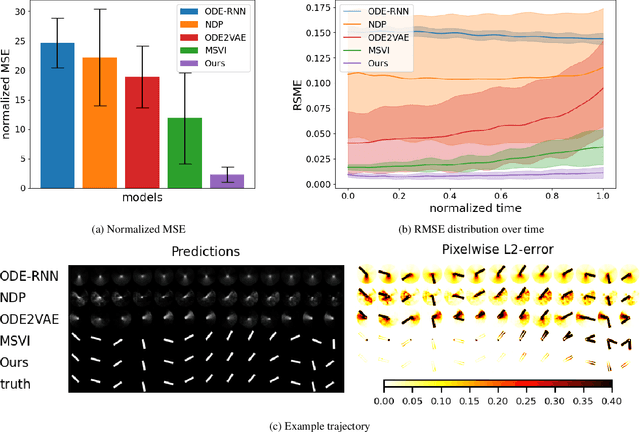
We propose a method for learning dynamical systems from high-dimensional empirical data that combines variational autoencoders and (spatio-)temporal attention within a framework designed to enforce certain scientifically-motivated invariances. We focus on the setting in which data are available from multiple different instances of a system whose underlying dynamical model is entirely unknown at the outset. The approach rests on a separation into an instance-specific encoding (capturing initial conditions, constants etc.) and a latent dynamics model that is itself universal across all instances/realizations of the system. The separation is achieved in an automated, data-driven manner and only empirical data are required as inputs to the model. The approach allows effective inference of system behaviour at any continuous time but does not require an explicit neural ODE formulation, which makes it efficient and highly scalable. We study behaviour through simple theoretical analyses and extensive experiments on synthetic and real-world datasets. The latter investigate learning the dynamics of complex systems based on finite data and show that the proposed approach can outperform state-of-the-art neural-dynamical models. We study also more general inductive bias in the context of transfer to data obtained under entirely novel system interventions. Overall, our results provide a promising new framework for efficiently learning dynamical models from heterogeneous data with potential applications in a wide range of fields including physics, medicine, biology and engineering.

Deep Learning of Causal Structures in High Dimensions

Recent years have seen rapid progress at the intersection between causality and machine learning. Motivated by scientific applications involving high-dimensional data, in particular in biomedicine, we propose a deep neural architecture for learning causal relationships between variables from a combination of empirical data and prior causal knowledge. We combine convolutional and graph neural networks within a causal risk framework to provide a flexible and scalable approach. Empirical results include linear and nonlinear simulations (where the underlying causal structures are known and can be directly compared against), as well as a real biological example where the models are applied to high-dimensional molecular data and their output compared against entirely unseen validation experiments. These results demonstrate the feasibility of using deep learning approaches to learn causal networks in large-scale problems spanning thousands of variables.

High-Dimensional Undirected Graphical Models for Arbitrary Mixed Data

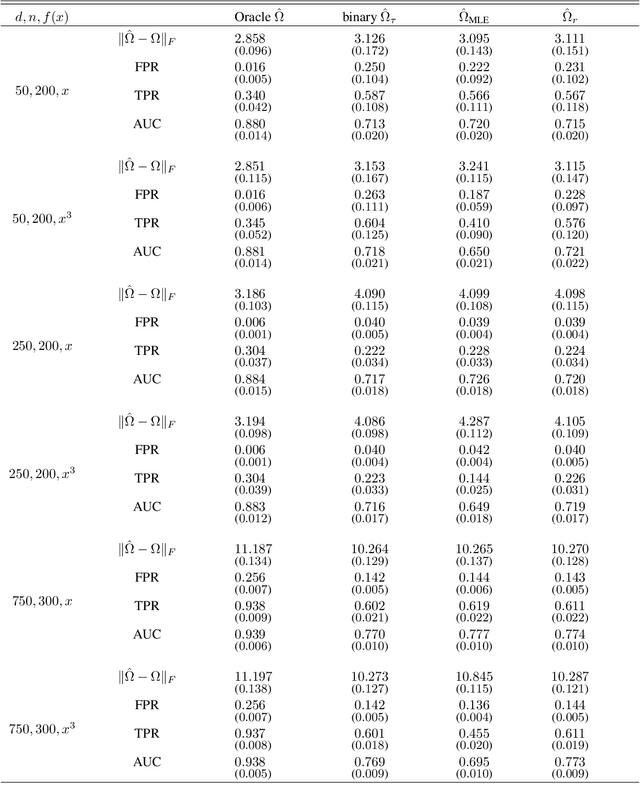
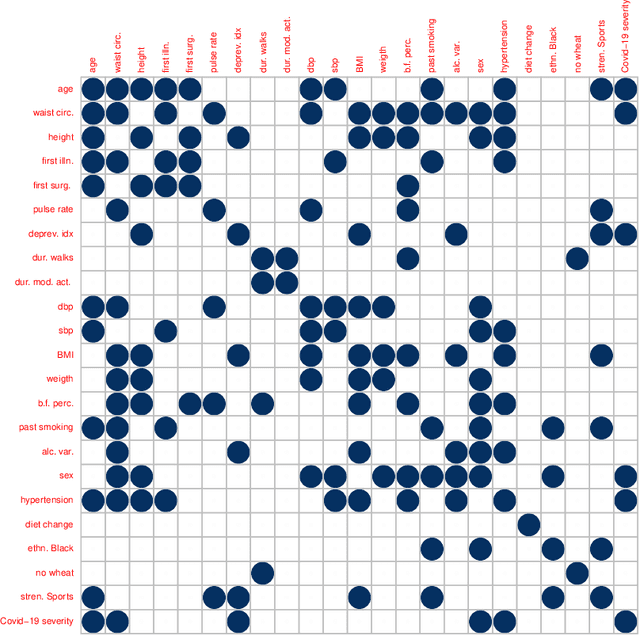
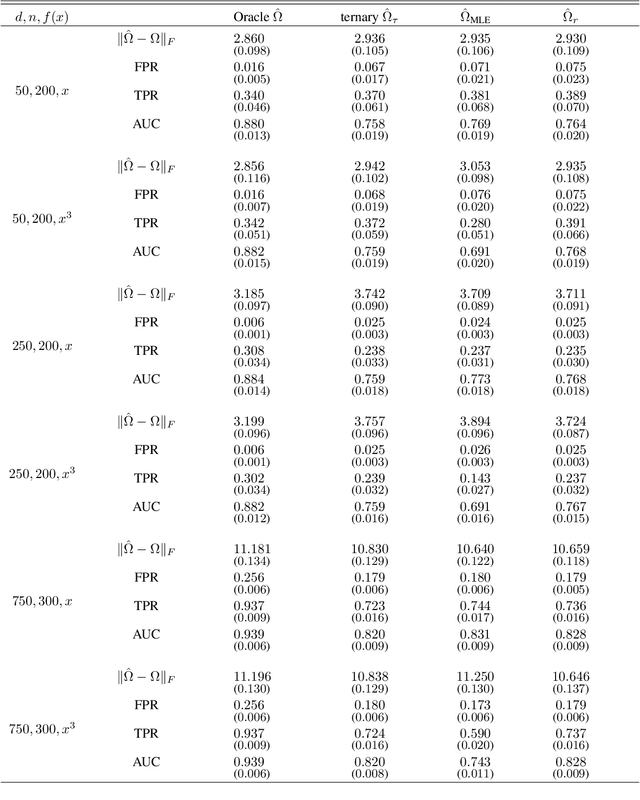
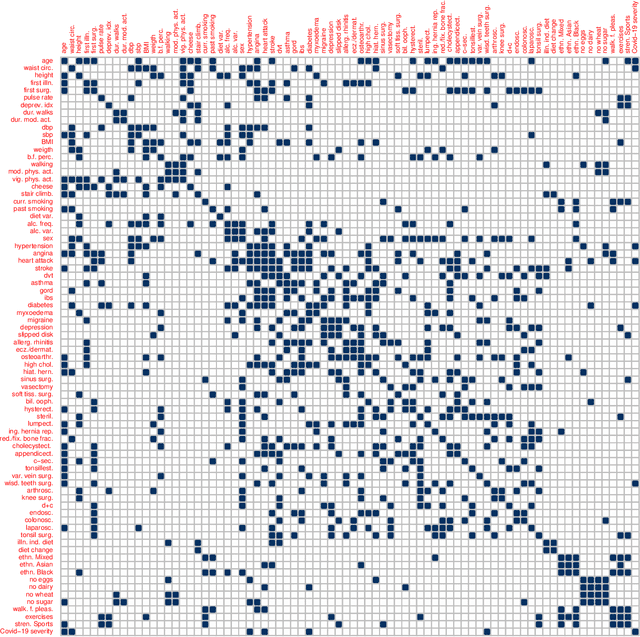
Graphical models are an important tool in exploring relationships between variables in complex, multivariate data. Methods for learning such graphical models are well developed in the case where all variables are either continuous or discrete, including in high-dimensions. However, in many applications data span variables of different types (e.g. continuous, count, binary, ordinal, etc.), whose principled joint analysis is nontrivial. Latent Gaussian copula models, in which all variables are modeled as transformations of underlying jointly Gaussian variables, represent a useful approach. Recent advances have shown how the binary-continuous case can be tackled, but the general mixed variable type regime remains challenging. In this work, we make the simple yet useful observation that classical ideas concerning polychoric and polyserial correlations can be leveraged in a latent Gaussian copula framework. Building on this observation we propose flexible and scalable methodology for data with variables of entirely general mixed type. We study the key properties of the approaches theoretically and empirically, via extensive simulations as well an illustrative application to data from the UK Biobank concerning COVID-19 risk factors.

Scalable Regularised Joint Mixture Models

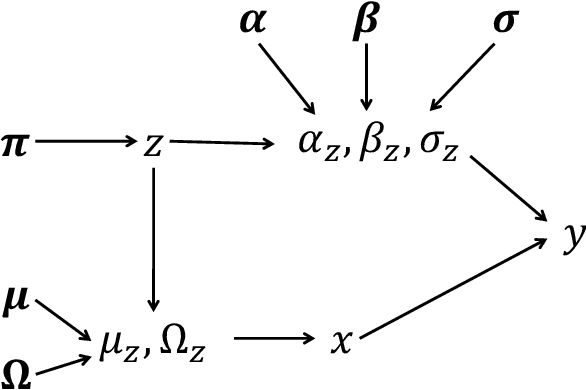
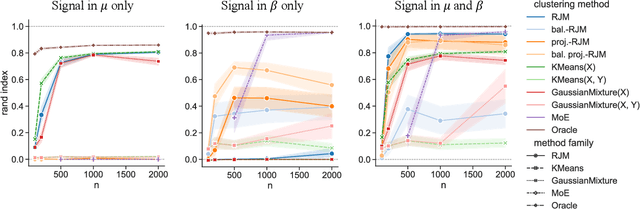
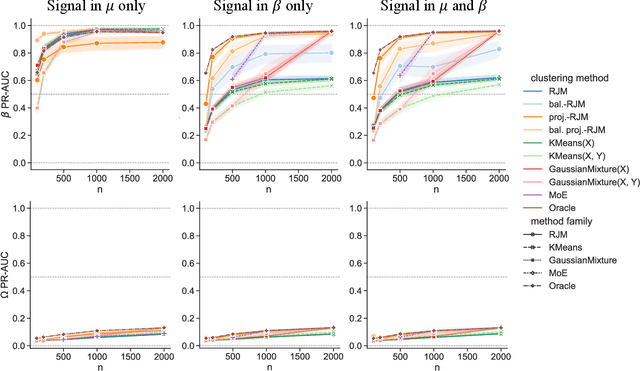
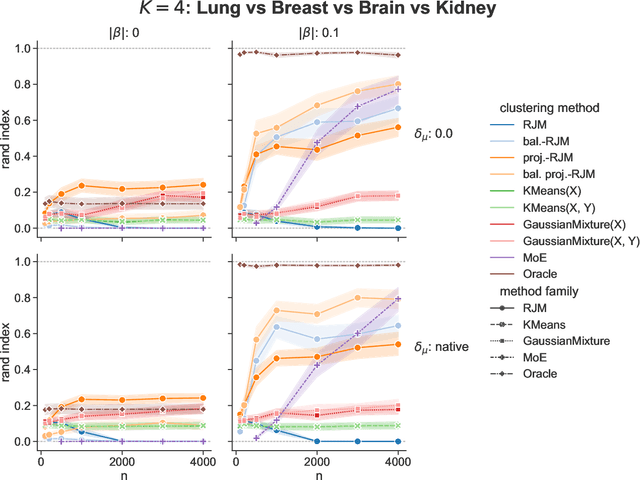
In many applications, data can be heterogeneous in the sense of spanning latent groups with different underlying distributions. When predictive models are applied to such data the heterogeneity can affect both predictive performance and interpretability. Building on developments at the intersection of unsupervised learning and regularised regression, we propose an approach for heterogeneous data that allows joint learning of (i) explicit multivariate feature distributions, (ii) high-dimensional regression models and (iii) latent group labels, with both (i) and (ii) specific to latent groups and both elements informing (iii). The approach is demonstrably effective in high dimensions, combining data reduction for computational efficiency with a re-weighting scheme that retains key signals even when the number of features is large. We discuss in detail these aspects and their impact on modelling and computation, including EM convergence. The approach is modular and allows incorporation of data reductions and high-dimensional estimators that are suitable for specific applications. We show results from extensive simulations and real data experiments, including highly non-Gaussian data. Our results allow efficient, effective analysis of high-dimensional data in settings, such as biomedicine, where both interpretable prediction and explicit feature space models are needed but hidden heterogeneity may be a concern.

On unsupervised projections and second order signals

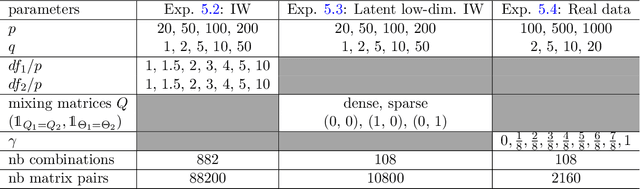
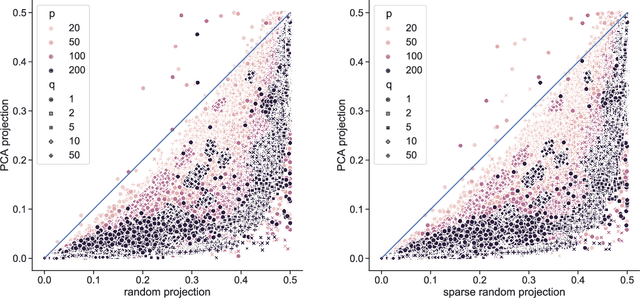
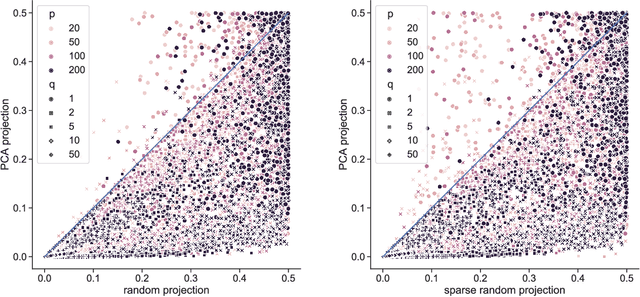
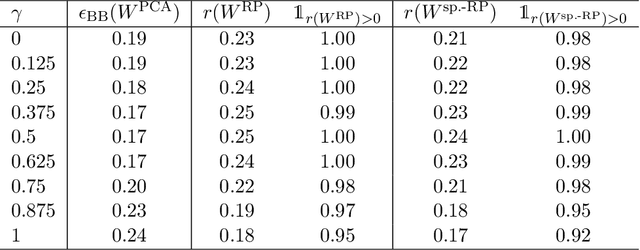
Linear projections are widely used in the analysis of high-dimensional data. In unsupervised settings where the data harbour latent classes/clusters, the question of whether class discriminatory signals are retained under projection is crucial. In the case of mean differences between classes, this question has been well studied. However, in many contemporary applications, notably in biomedicine, group differences at the level of covariance or graphical model structure are important. Motivated by such applications, in this paper we ask whether linear projections can preserve differences in second order structure between latent groups. We focus on unsupervised projections, which can be computed without knowledge of class labels. We discuss a simple theoretical framework to study the behaviour of such projections which we use to inform an analysis via quasi-exhaustive enumeration. This allows us to consider the performance, over more than a hundred thousand sets of data-generating population parameters, of two popular projections, namely random projections (RP) and Principal Component Analysis (PCA). Across this broad range of regimes, PCA turns out to be more effective at retaining second order signals than RP and is often even competitive with supervised projection. We complement these results with fully empirical experiments showing 0-1 loss using simulated and real data. We study also the effect of projection dimension, drawing attention to a bias-variance trade-off in this respect. Our results show that PCA can indeed be a suitable first-step for unsupervised analysis, including in cases where differential covariance or graphical model structure are of interest.

Ancestral causal learning in high dimensions with a human genome-wide application

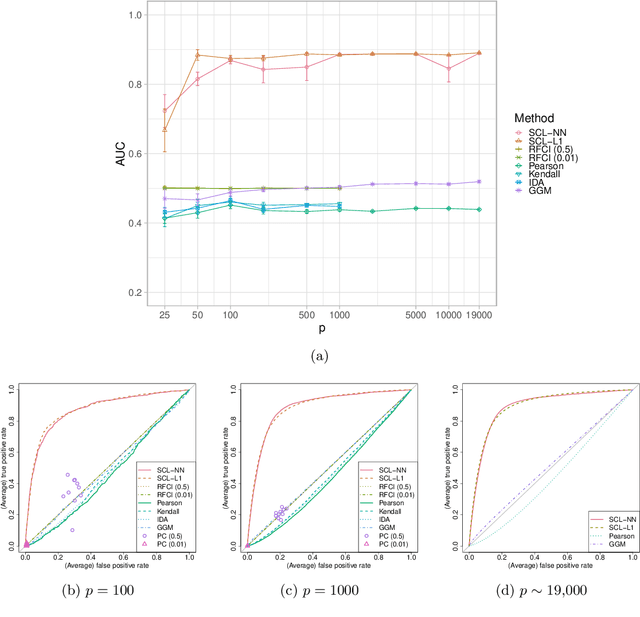
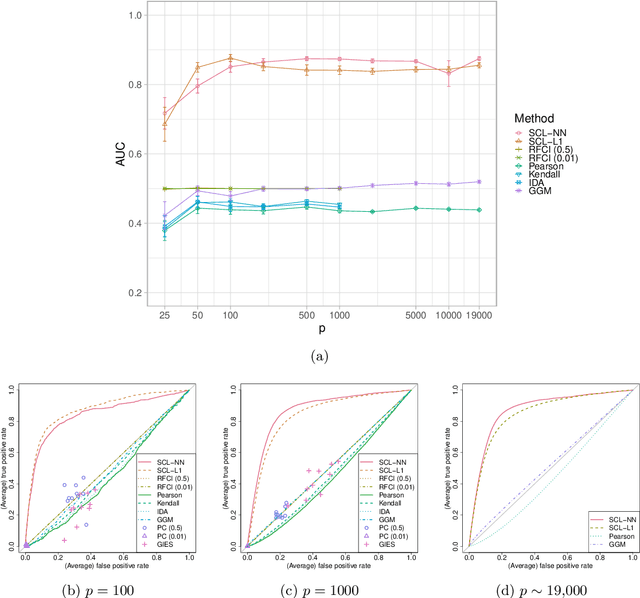
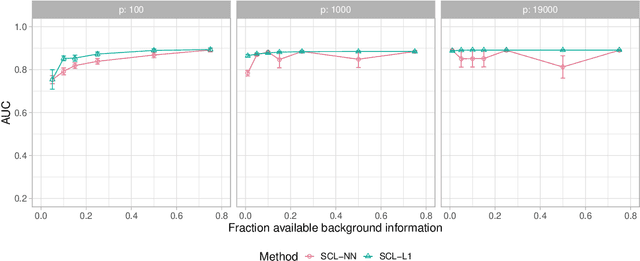
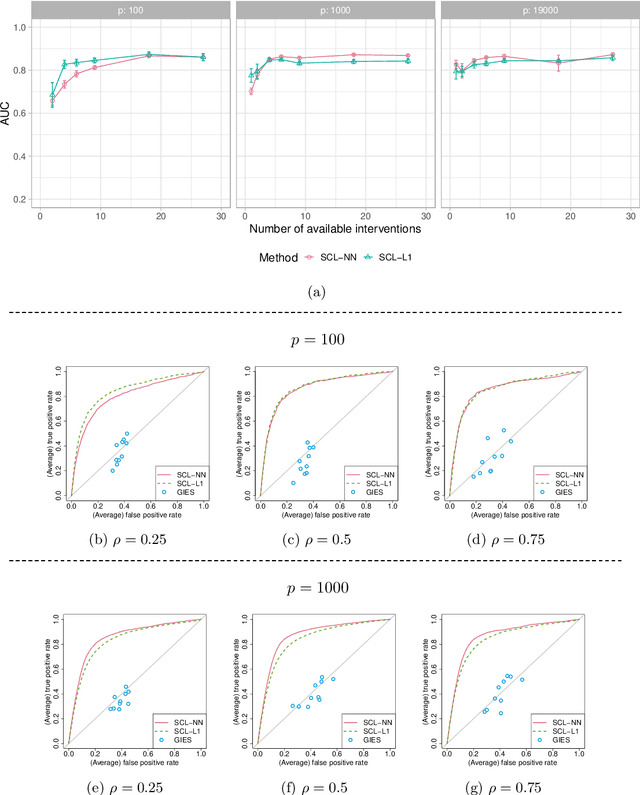
We consider learning ancestral causal relationships in high dimensions. Our approach is driven by a supervised learning perspective, with discrete indicators of causal relationships treated as labels to be learned from available data. We focus on the setting in which some causal (ancestral) relationships are known (via background knowledge or experimental data) and put forward a general approach that scales to large problems. This is motivated by problems in human biology which are characterized by high dimensionality and potentially many latent variables. We present a case study involving interventional data from human cells with total dimension $p \! \sim \! 19{,}000$. Performance is assessed empirically by testing model output against previously unseen interventional data. The proposed approach is highly effective and demonstrably scalable to the human genome-wide setting. We consider sensitivity to background knowledge and find that results are robust to nontrivial perturbations of the input information. We consider also the case, relevant to some applications, where the only prior information available concerns a small number of known ancestral relationships.

Model-based clustering in very high dimensions via adaptive projections

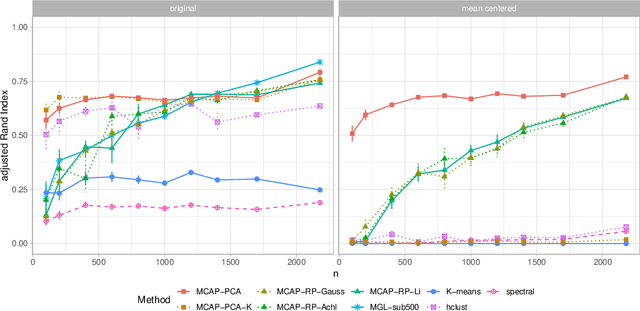
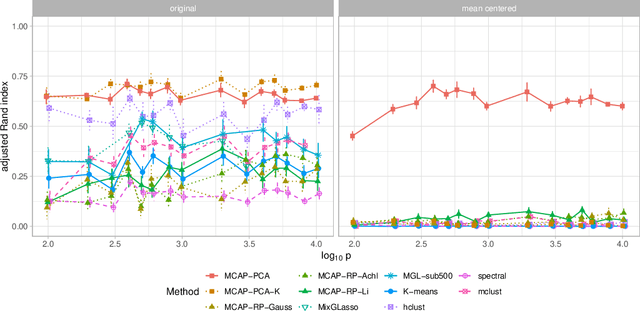
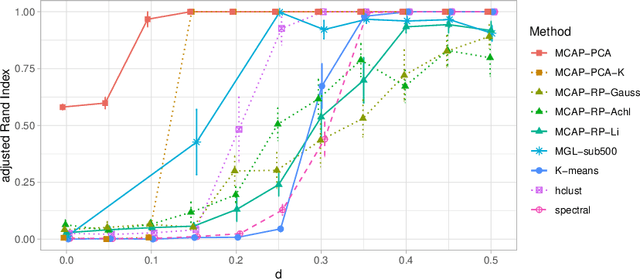
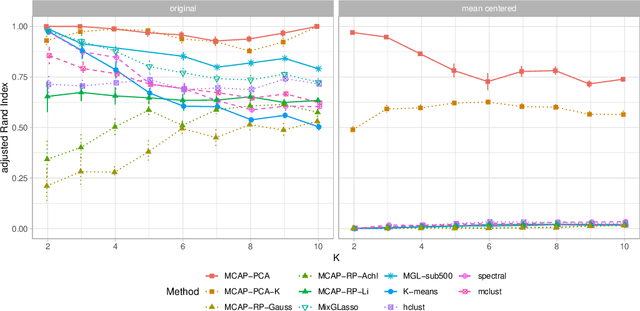
Mixture models are a standard approach to dealing with heterogeneous data with non-i.i.d. structure. However, when the dimension $p$ is large relative to sample size $n$ and where either or both of means and covariances/graphical models may differ between the latent groups, mixture models face statistical and computational difficulties and currently available methods cannot realistically go beyond $p \! \sim \! 10^4$ or so. We propose an approach called Model-based Clustering via Adaptive Projections (MCAP). Instead of estimating mixtures in the original space, we work with a low-dimensional representation obtained by linear projection. The projection dimension itself plays an important role and governs a type of bias-variance tradeoff with respect to recovery of the relevant signals. MCAP sets the projection dimension automatically in a data-adaptive manner, using a proxy for the assignment risk. Combining a full covariance formulation with the adaptive projection allows detection of both mean and covariance signals in very high dimensional problems. We show real-data examples in which covariance signals are reliably detected in problems with $p \! \sim \! 10^4$ or more, and simulations going up to $p = 10^6$. In some examples, MCAP performs well even when the mean signal is entirely removed, leaving differential covariance structure in the high-dimensional space as the only signal. Across a number of regimes, MCAP performs as well or better than a range of existing methods, including a recently-proposed $\ell_1$-penalized approach; and performance remains broadly stable with increasing dimension. MCAP can be run "out of the box" and is fast enough for interactive use on large-$p$ problems using standard desktop computing resources.

High-dimensional regression in practice: an empirical study of finite-sample prediction, variable selection and ranking

Penalized likelihood methods are widely used for high-dimensional regression. Although many methods have been proposed and the associated theory is now well-developed, the relative efficacy of different methods in finite-sample settings, as encountered in practice, remains incompletely understood. There is therefore a need for empirical investigations in this area that can offer practical insight and guidance to users of these methods. In this paper we present a large-scale comparison of penalized regression methods. We distinguish between three related goals: prediction, variable selection and variable ranking. Our results span more than 1,800 data-generating scenarios, allowing us to systematically consider the influence of various factors (sample size, dimensionality, sparsity, signal strength and multicollinearity). We consider several widely-used methods (Lasso, Elastic Net, Ridge Regression, SCAD, the Dantzig Selector as well as Stability Selection). We find considerable variation in performance between methods, with results dependent on details of the data-generating scenario and the specific goal. Our results support a `no panacea' view, with no unambiguous winner across all scenarios, even in this restricted setting where all data align well with the assumptions underlying the methods. Lasso is well-behaved, performing competitively in many scenarios, while SCAD is highly variable. Substantial benefits from a Ridge-penalty are only seen in the most challenging scenarios with strong multi-collinearity. The results are supported by semi-synthetic analyzes using gene expression data from cancer samples. Our empirical results complement existing theory and provide a resource to compare methods across a range of scenarios and metrics.