Scalable Regularised Joint Mixture Models

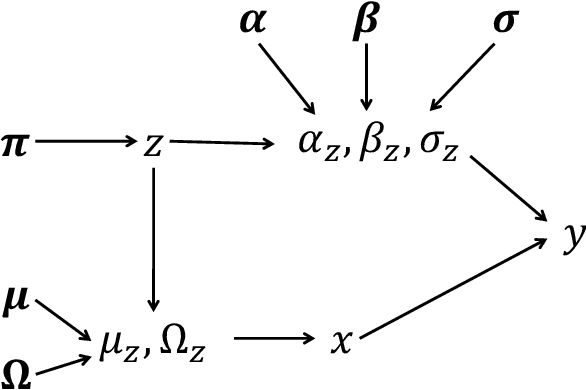
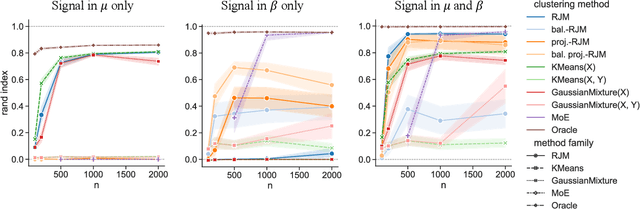
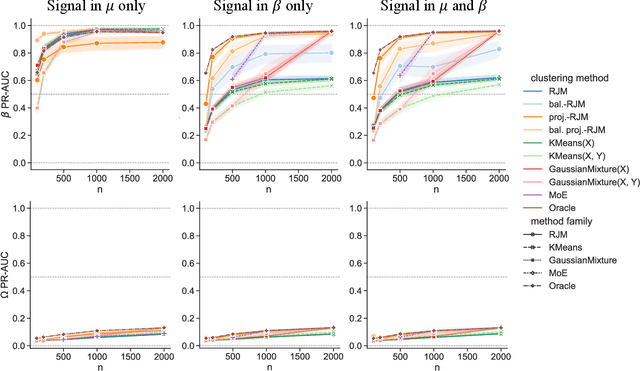
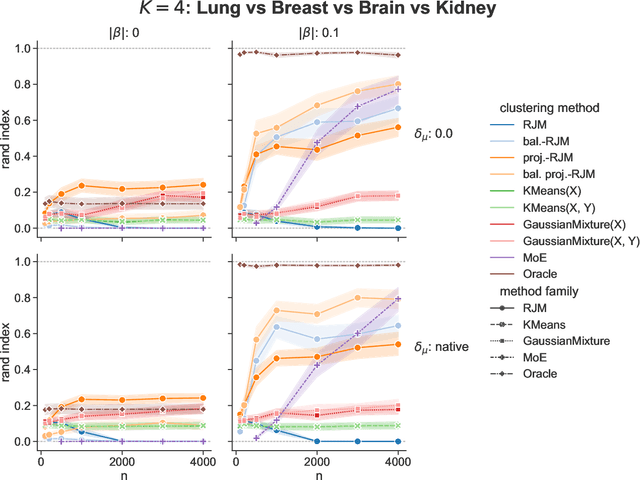
In many applications, data can be heterogeneous in the sense of spanning latent groups with different underlying distributions. When predictive models are applied to such data the heterogeneity can affect both predictive performance and interpretability. Building on developments at the intersection of unsupervised learning and regularised regression, we propose an approach for heterogeneous data that allows joint learning of (i) explicit multivariate feature distributions, (ii) high-dimensional regression models and (iii) latent group labels, with both (i) and (ii) specific to latent groups and both elements informing (iii). The approach is demonstrably effective in high dimensions, combining data reduction for computational efficiency with a re-weighting scheme that retains key signals even when the number of features is large. We discuss in detail these aspects and their impact on modelling and computation, including EM convergence. The approach is modular and allows incorporation of data reductions and high-dimensional estimators that are suitable for specific applications. We show results from extensive simulations and real data experiments, including highly non-Gaussian data. Our results allow efficient, effective analysis of high-dimensional data in settings, such as biomedicine, where both interpretable prediction and explicit feature space models are needed but hidden heterogeneity may be a concern.

On unsupervised projections and second order signals

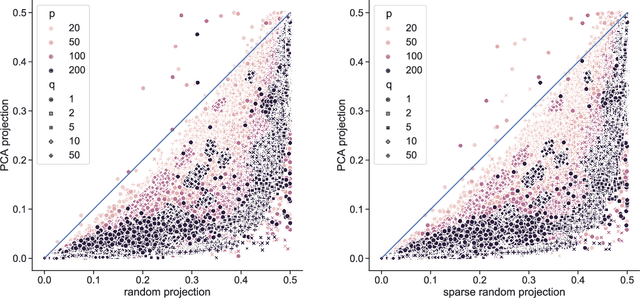
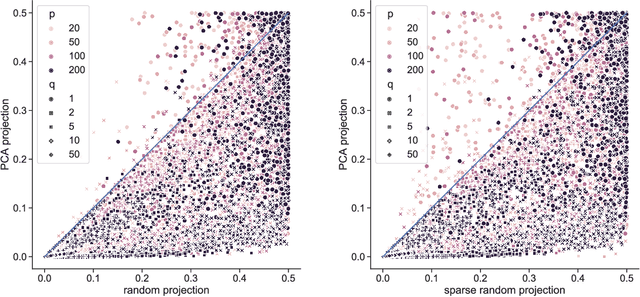
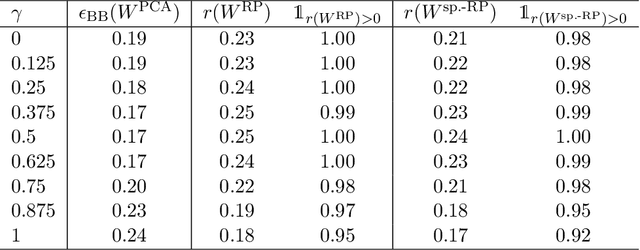
Linear projections are widely used in the analysis of high-dimensional data. In unsupervised settings where the data harbour latent classes/clusters, the question of whether class discriminatory signals are retained under projection is crucial. In the case of mean differences between classes, this question has been well studied. However, in many contemporary applications, notably in biomedicine, group differences at the level of covariance or graphical model structure are important. Motivated by such applications, in this paper we ask whether linear projections can preserve differences in second order structure between latent groups. We focus on unsupervised projections, which can be computed without knowledge of class labels. We discuss a simple theoretical framework to study the behaviour of such projections which we use to inform an analysis via quasi-exhaustive enumeration. This allows us to consider the performance, over more than a hundred thousand sets of data-generating population parameters, of two popular projections, namely random projections (RP) and Principal Component Analysis (PCA). Across this broad range of regimes, PCA turns out to be more effective at retaining second order signals than RP and is often even competitive with supervised projection. We complement these results with fully empirical experiments showing 0-1 loss using simulated and real data. We study also the effect of projection dimension, drawing attention to a bias-variance trade-off in this respect. Our results show that PCA can indeed be a suitable first-step for unsupervised analysis, including in cases where differential covariance or graphical model structure are of interest.

Mixture of Conditional Gaussian Graphical Models for unlabelled heterogeneous populations in the presence of co-factors

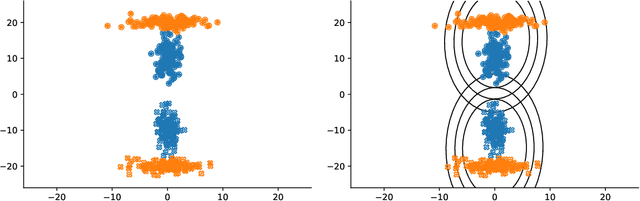
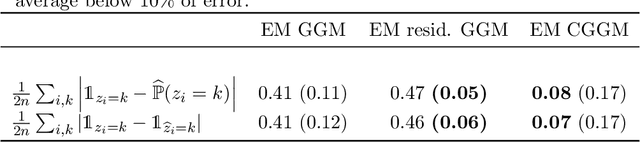
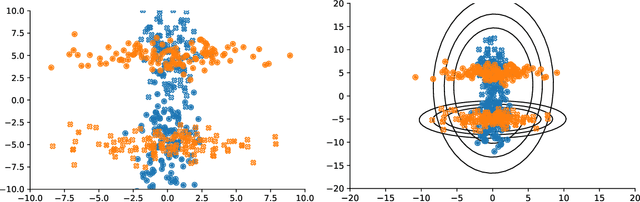
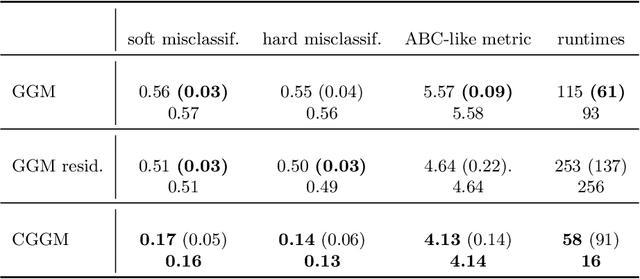
Conditional correlation networks, within Gaussian Graphical Models (GGM), are widely used to describe the direct interactions between the components of a random vector. In the case of an unlabelled Heterogeneous population, Expectation Maximisation (EM) algorithms for Mixtures of GGM have been proposed to estimate both each sub-population's graph and the class labels. However, we argue that, with most real data, class affiliation cannot be described with a Mixture of Gaussian, which mostly groups data points according to their geometrical proximity. In particular, there often exists external co-features whose values affect the features' average value, scattering across the feature space data points belonging to the same sub-population. Additionally, if the co-features' effect on the features is Heterogeneous, then the estimation of this effect cannot be separated from the sub-population identification. In this article, we propose a Mixture of Conditional GGM (CGGM) that subtracts the heterogeneous effects of the co-features to regroup the data points into sub-population corresponding clusters. We develop a penalised EM algorithm to estimate graph-sparse model parameters. We demonstrate on synthetic and real data how this method fulfils its goal and succeeds in identifying the sub-populations where the Mixtures of GGM are disrupted by the effect of the co-features.

Deterministic Approximate EM Algorithm; Application to the Riemann Approximation EM and the Tempered EM

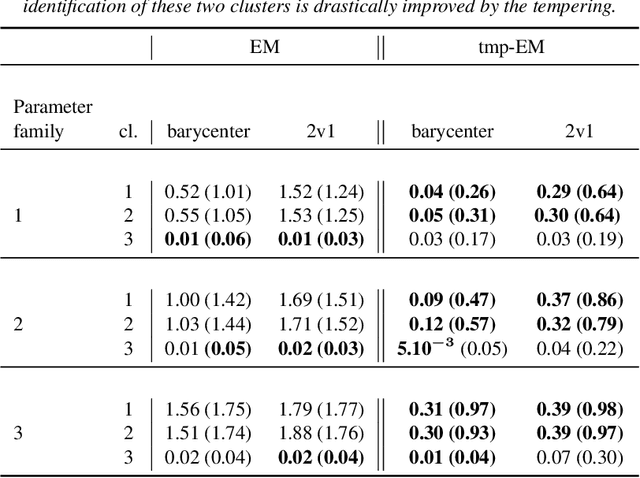
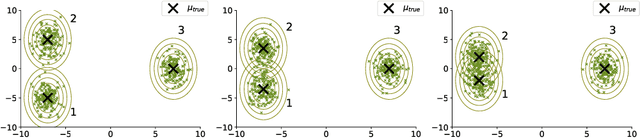
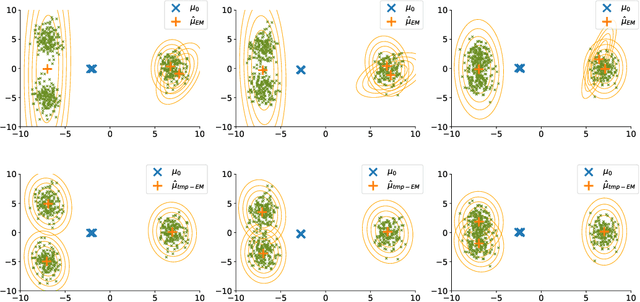
The Expectation Maximisation (EM) algorithm is widely used to optimise non-convex likelihood functions with hidden variables. Many authors modified its simple design to fit more specific situations. For instance the Expectation (E) step has been replaced by Monte Carlo (MC) approximations, Markov Chain Monte Carlo approximations, tempered approximations... Most of the well studied approximations belong to the stochastic class. By comparison, the literature is lacking when it comes to deterministic approximations. In this paper, we introduce a theoretical framework, with state of the art convergence guarantees, for any deterministic approximation of the E step. We analyse theoretically and empirically several approximations that fit into this framework. First, for cases with intractable E steps, we introduce a deterministic alternative to the MC-EM, using Riemann sums. This method is easy to implement and does not require the tuning of hyper-parameters. Then, we consider the tempered approximation, borrowed from the Simulated Annealing optimisation technique and meant to improve the EM solution. We prove that the the tempered EM verifies the convergence guarantees for a wide range of temperature profiles. We showcase empirically how it is able to escape adversarial initialisations. Finally, we combine the Riemann and tempered approximations to accomplish both their purposes.

Gaussian Graphical Model exploration and selection in high dimension low sample size setting

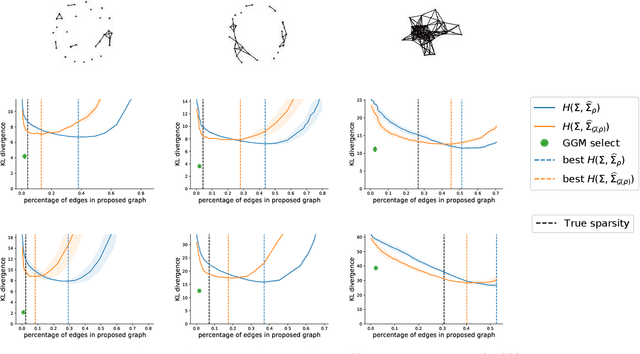
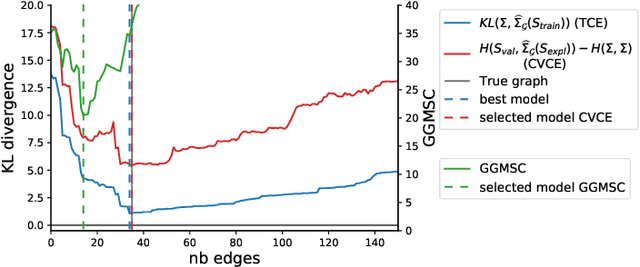
Gaussian Graphical Models (GGM) are often used to describe the conditional correlations between the components of a random vector. In this article, we compare two families of GGM inference methods: nodewise edge selection and penalised likelihood maximisation. We demonstrate on synthetic data that, when the sample size is small, the two methods produce graphs with either too few or too many edges when compared to the real one. As a result, we propose a composite procedure that explores a family of graphs with an nodewise numerical scheme and selects a candidate among them with an overall likelihood criterion. We demonstrate that, when the number of observations is small, this selection method yields graphs closer to the truth and corresponding to distributions with better KL divergence with regards to the real distribution than the other two. Finally, we show the interest of our algorithm on two concrete cases: first on brain imaging data, then on biological nephrology data. In both cases our results are more in line with current knowledge in each field.