T-Rep: Representation Learning for Time Series using Time-Embeddings

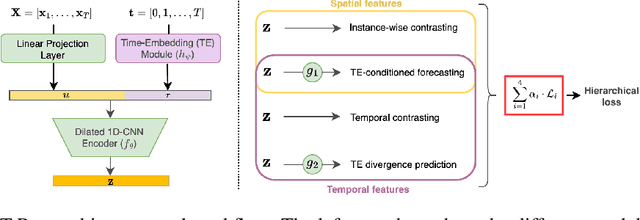
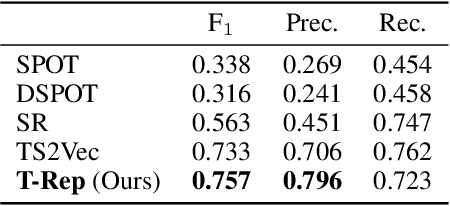
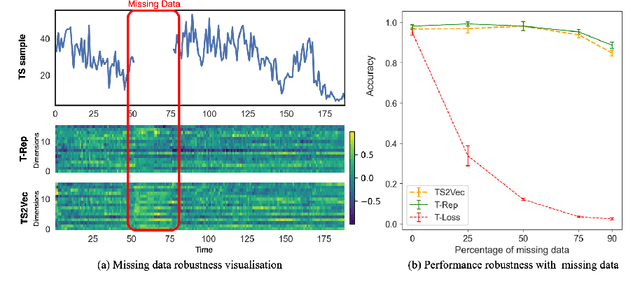
Multivariate time series present challenges to standard machine learning techniques, as they are often unlabeled, high dimensional, noisy, and contain missing data. To address this, we propose T-Rep, a self-supervised method to learn time series representations at a timestep granularity. T-Rep learns vector embeddings of time alongside its feature extractor, to extract temporal features such as trend, periodicity, or distribution shifts from the signal. These time-embeddings are leveraged in pretext tasks, to incorporate smooth and fine-grained temporal dependencies in the representations, as well as reinforce robustness to missing data. We evaluate T-Rep on downstream classification, forecasting, and anomaly detection tasks. It is compared to existing self-supervised algorithms for time series, which it outperforms in all three tasks. We test T-Rep in missing data regimes, where it proves more resilient than its counterparts. Finally, we provide latent space visualisation experiments, highlighting the interpretability of the learned representations.

Improving Multimodal Joint Variational Autoencoders through Normalizing Flows and Correlation Analysis

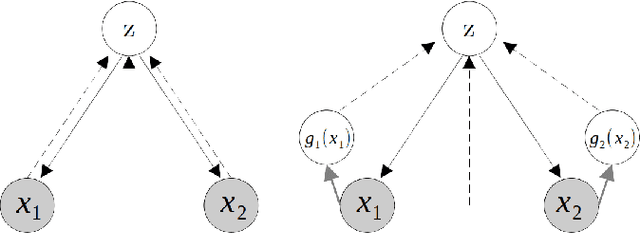
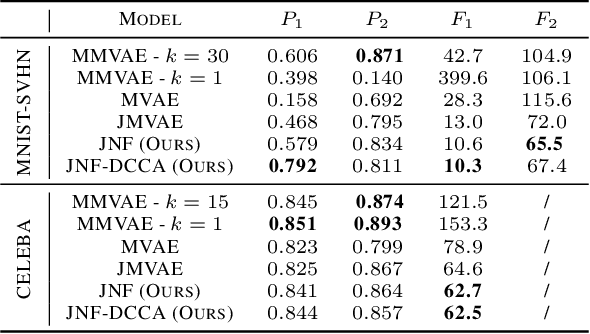
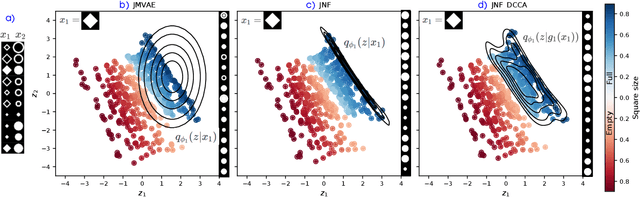
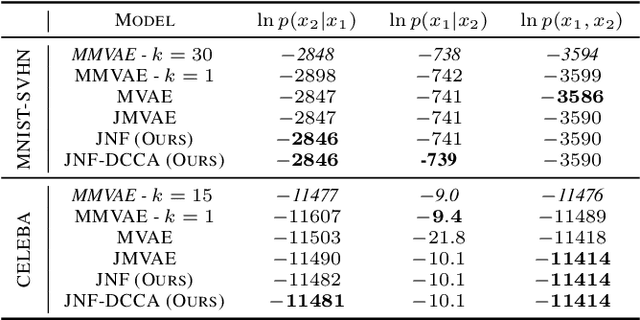
We propose a new multimodal variational autoencoder that enables to generate from the joint distribution and conditionally to any number of complex modalities. The unimodal posteriors are conditioned on the Deep Canonical Correlation Analysis embeddings which preserve the shared information across modalities leading to more coherent cross-modal generations. Furthermore, we use Normalizing Flows to enrich the unimodal posteriors and achieve more diverse data generation. Finally, we propose to use a Product of Experts for inferring one modality from several others which makes the model scalable to any number of modalities. We demonstrate that our method improves likelihood estimates, diversity of the generations and in particular coherence metrics in the conditional generations on several datasets.

Variational Inference for Longitudinal Data Using Normalizing Flows

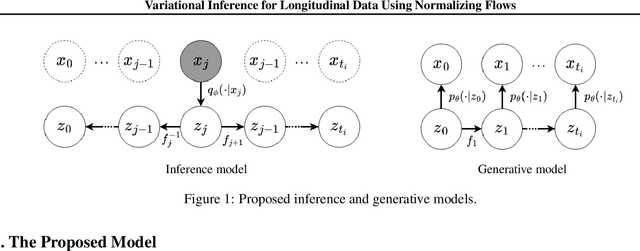
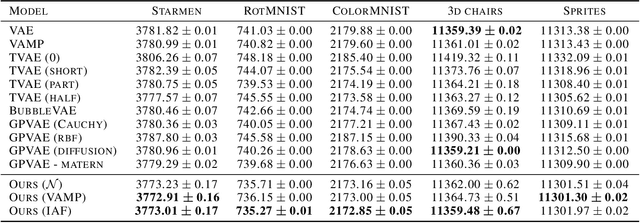
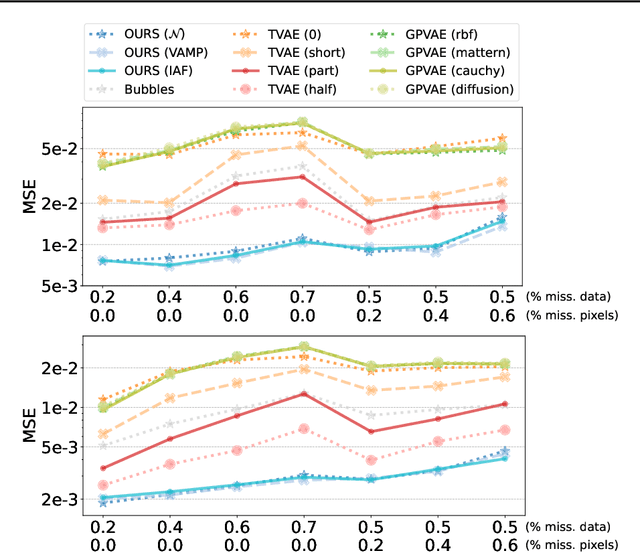
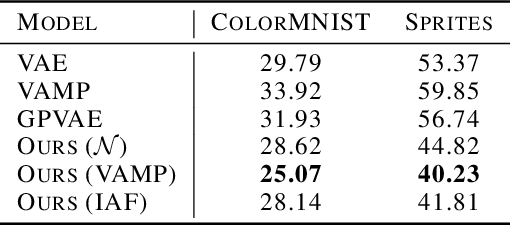
This paper introduces a new latent variable generative model able to handle high dimensional longitudinal data and relying on variational inference. The time dependency between the observations of an input sequence is modelled using normalizing flows over the associated latent variables. The proposed method can be used to generate either fully synthetic longitudinal sequences or trajectories that are conditioned on several data in a sequence and demonstrates good robustness properties to missing data. We test the model on 6 datasets of different complexity and show that it can achieve better likelihood estimates than some competitors as well as more reliable missing data imputation. A code is made available at \url{https://github.com/clementchadebec/variational_inference_for_longitudinal_data}.

A Geometric Perspective on Variational Autoencoders

This paper introduces a new interpretation of the Variational Autoencoder framework by taking a fully geometric point of view. We argue that vanilla VAE models unveil naturally a Riemannian structure in their latent space and that taking into consideration those geometrical aspects can lead to better interpolations and an improved generation procedure. This new proposed sampling method consists in sampling from the uniform distribution deriving intrinsically from the learned Riemannian latent space and we show that using this scheme can make a vanilla VAE competitive and even better than more advanced versions on several benchmark datasets. Since generative models are known to be sensitive to the number of training samples we also stress the method's robustness in the low data regime.

Pythae: Unifying Generative Autoencoders in Python -- A Benchmarking Use Case

In recent years, deep generative models have attracted increasing interest due to their capacity to model complex distributions. Among those models, variational autoencoders have gained popularity as they have proven both to be computationally efficient and yield impressive results in multiple fields. Following this breakthrough, extensive research has been done in order to improve the original publication, resulting in a variety of different VAE models in response to different tasks. In this paper we present Pythae, a versatile open-source Python library providing both a unified implementation and a dedicated framework allowing straightforward, reproducible and reliable use of generative autoencoder models. We then propose to use this library to perform a case study benchmark where we present and compare 19 generative autoencoder models representative of some of the main improvements on downstream tasks such as image reconstruction, generation, classification, clustering and interpolation. The open-source library can be found at https://github.com/clementchadebec/benchmark_VAE.

Data Augmentation in High Dimensional Low Sample Size Setting Using a Geometry-Based Variational Autoencoder

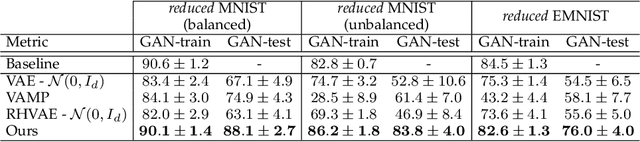
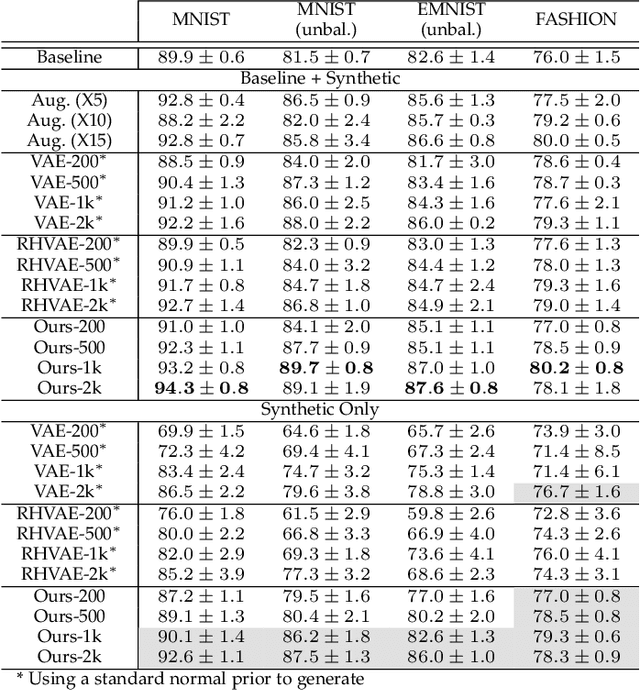
In this paper, we propose a new method to perform data augmentation in a reliable way in the High Dimensional Low Sample Size (HDLSS) setting using a geometry-based variational autoencoder. Our approach combines a proper latent space modeling of the VAE seen as a Riemannian manifold with a new generation scheme which produces more meaningful samples especially in the context of small data sets. The proposed method is tested through a wide experimental study where its robustness to data sets, classifiers and training samples size is stressed. It is also validated on a medical imaging classification task on the challenging ADNI database where a small number of 3D brain MRIs are considered and augmented using the proposed VAE framework. In each case, the proposed method allows for a significant and reliable gain in the classification metrics. For instance, balanced accuracy jumps from 66.3% to 74.3% for a state-of-the-art CNN classifier trained with 50 MRIs of cognitively normal (CN) and 50 Alzheimer disease (AD) patients and from 77.7% to 86.3% when trained with 243 CN and 210 AD while improving greatly sensitivity and specificity metrics.

Data Generation in Low Sample Size Setting Using Manifold Sampling and a Geometry-Aware VAE

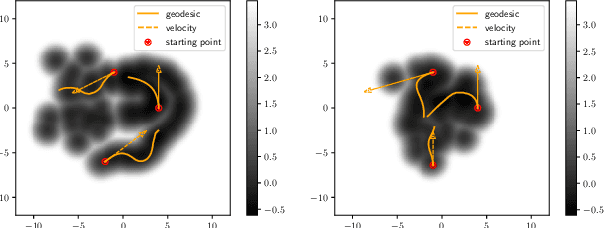
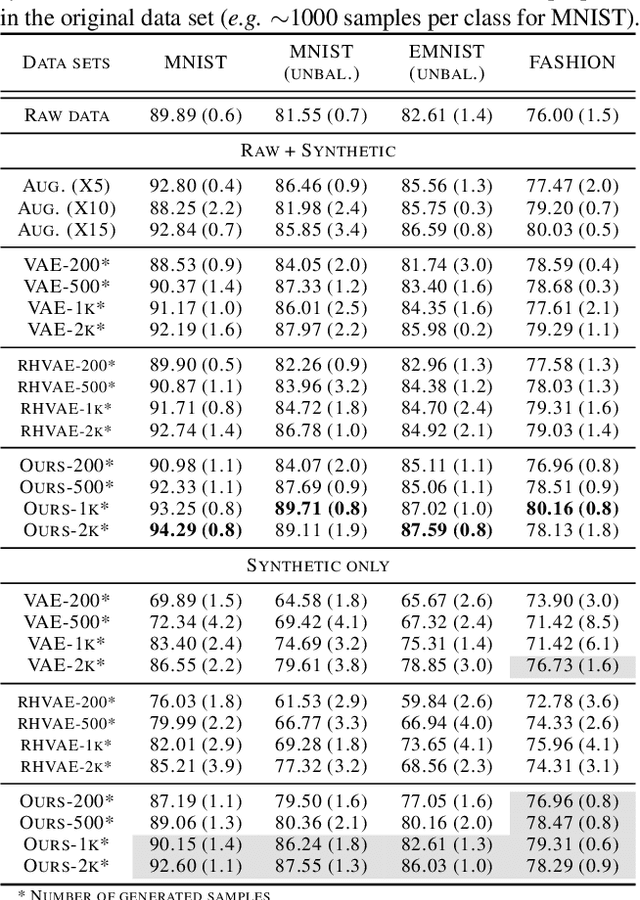
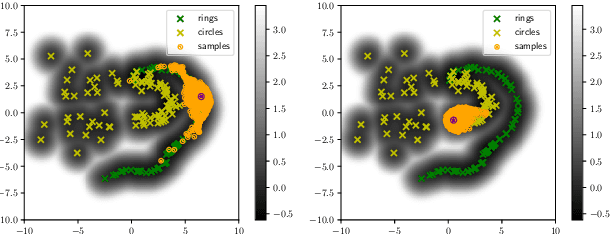
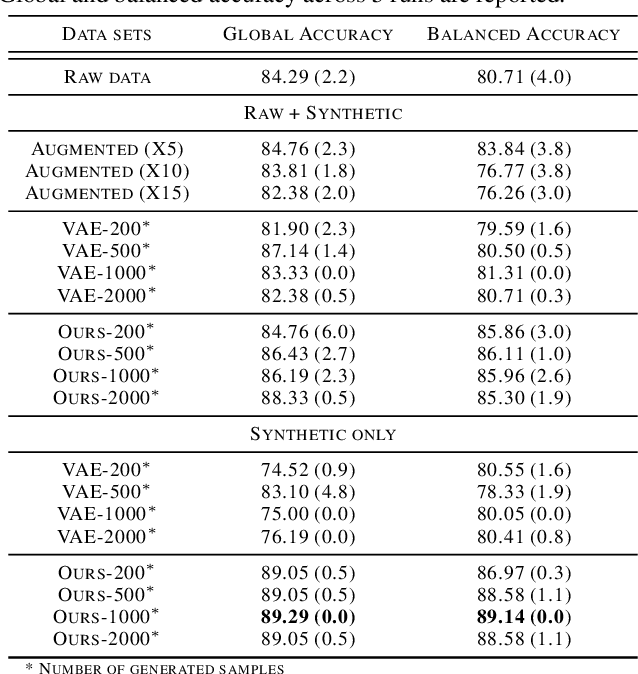
While much efforts have been focused on improving Variational Autoencoders through richer posterior and prior distributions, little interest was shown in amending the way we generate the data. In this paper, we develop two non \emph{prior-dependent} generation procedures based on the geometry of the latent space seen as a Riemannian manifold. The first one consists in sampling along geodesic paths which is a natural way to explore the latent space while the second one consists in sampling from the inverse of the metric volume element which is easier to use in practice. Both methods are then compared to \emph{prior-based} methods on various data sets and appear well suited for a limited data regime. Finally, the latter method is used to perform data augmentation in a small sample size setting and is validated across various standard and \emph{real-life} data sets. In particular, this scheme allows to greatly improve classification results on the OASIS database where balanced accuracy jumps from 80.7% for a classifier trained with the raw data to 89.1% when trained only with the synthetic data generated by our method. Such results were also observed on 4 standard data sets.

Optimisation des parcours patients pour lutter contre l'errance de diagnostic des patients atteints de maladies rares

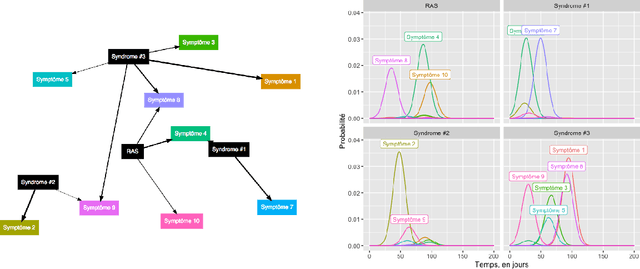
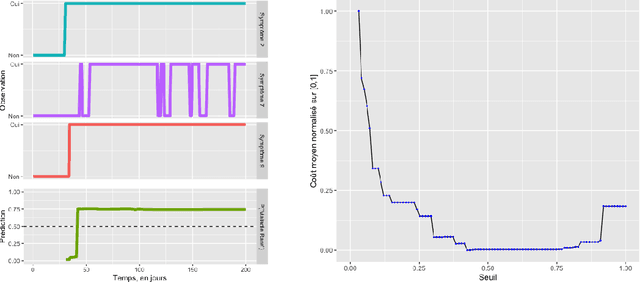
A patient suffering from a rare disease in France has to wait an average of two years before being diagnosed. This medical wandering is highly detrimental both for the health system and for patients whose pathology may worsen. There exists an efficient network of Centres of Reference for Rare Diseases (CRMR), but patients are often referred to these structures too late. We are considering a probabilistic modelling of the patient pathway in order to create a simulator that will allow us to create an alert system that detects wandering patients and refers them to a CRMR while considering the potential additional costs associated with these decisions.

Geometry-Aware Hamiltonian Variational Auto-Encoder

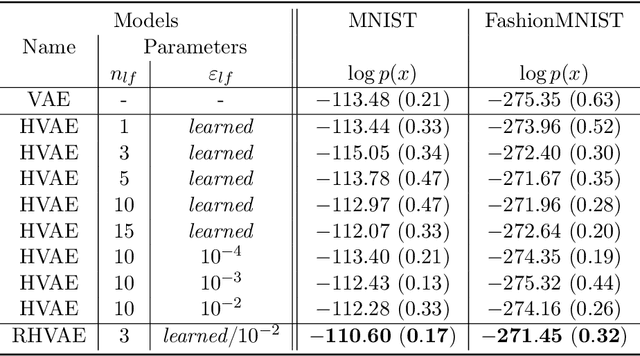
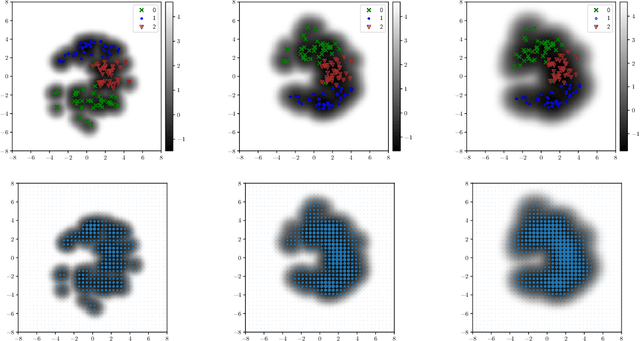
Variational auto-encoders (VAEs) have proven to be a well suited tool for performing dimensionality reduction by extracting latent variables lying in a potentially much smaller dimensional space than the data. Their ability to capture meaningful information from the data can be easily apprehended when considering their capability to generate new realistic samples or perform potentially meaningful interpolations in a much smaller space. However, such generative models may perform poorly when trained on small data sets which are abundant in many real-life fields such as medicine. This may, among others, come from the lack of structure of the latent space, the geometry of which is often under-considered. We thus propose in this paper to see the latent space as a Riemannian manifold endowed with a parametrized metric learned at the same time as the encoder and decoder networks. This metric is then used in what we called the Riemannian Hamiltonian VAE which extends the Hamiltonian VAE introduced by arXiv:1805.11328 to better exploit the underlying geometry of the latent space. We argue that such latent space modelling provides useful information about its underlying structure leading to far more meaningful interpolations, more realistic data-generation and more reliable clustering.

Mixture of Conditional Gaussian Graphical Models for unlabelled heterogeneous populations in the presence of co-factors

Conditional correlation networks, within Gaussian Graphical Models (GGM), are widely used to describe the direct interactions between the components of a random vector. In the case of an unlabelled Heterogeneous population, Expectation Maximisation (EM) algorithms for Mixtures of GGM have been proposed to estimate both each sub-population's graph and the class labels. However, we argue that, with most real data, class affiliation cannot be described with a Mixture of Gaussian, which mostly groups data points according to their geometrical proximity. In particular, there often exists external co-features whose values affect the features' average value, scattering across the feature space data points belonging to the same sub-population. Additionally, if the co-features' effect on the features is Heterogeneous, then the estimation of this effect cannot be separated from the sub-population identification. In this article, we propose a Mixture of Conditional GGM (CGGM) that subtracts the heterogeneous effects of the co-features to regroup the data points into sub-population corresponding clusters. We develop a penalised EM algorithm to estimate graph-sparse model parameters. We demonstrate on synthetic and real data how this method fulfils its goal and succeeds in identifying the sub-populations where the Mixtures of GGM are disrupted by the effect of the co-features.