High-dimensional regression in practice: an empirical study of finite-sample prediction, variable selection and ranking

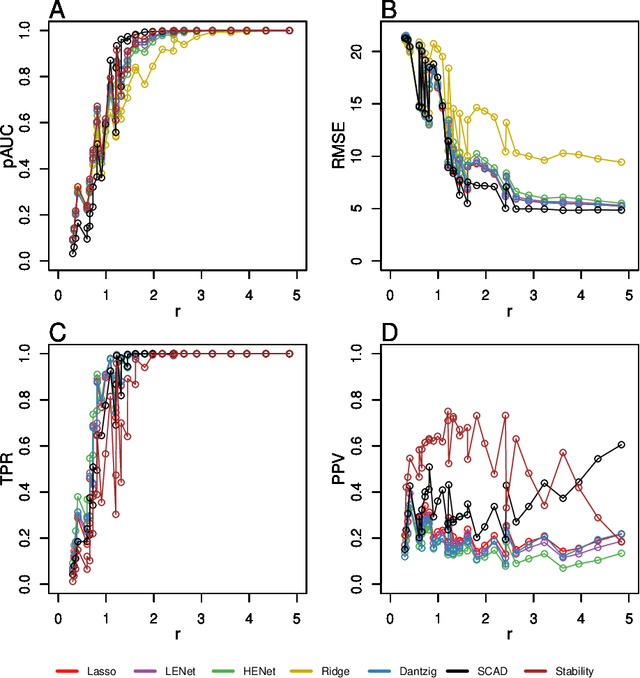
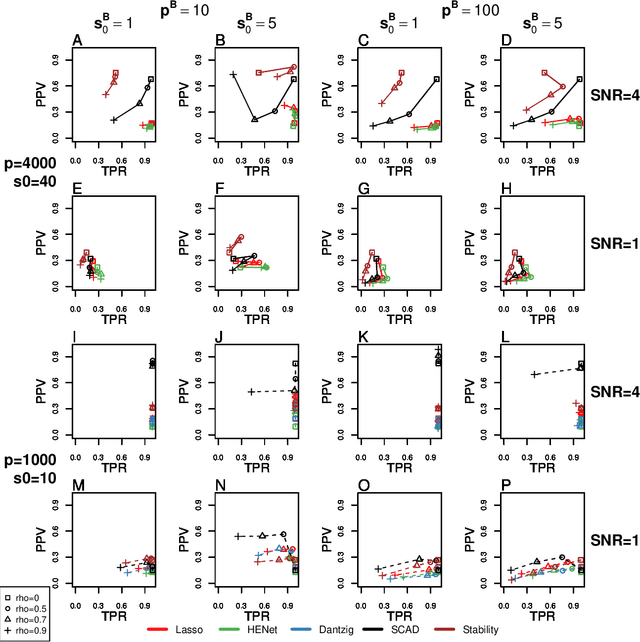
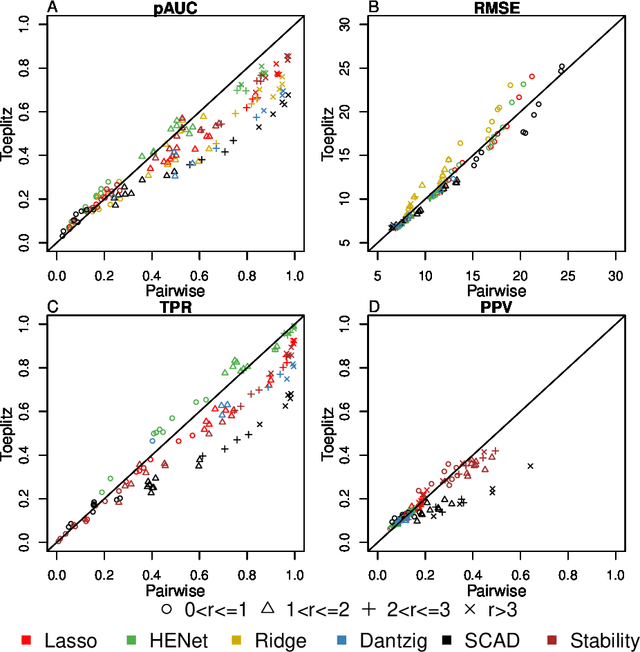
Penalized likelihood methods are widely used for high-dimensional regression. Although many methods have been proposed and the associated theory is now well-developed, the relative efficacy of different methods in finite-sample settings, as encountered in practice, remains incompletely understood. There is therefore a need for empirical investigations in this area that can offer practical insight and guidance to users of these methods. In this paper we present a large-scale comparison of penalized regression methods. We distinguish between three related goals: prediction, variable selection and variable ranking. Our results span more than 1,800 data-generating scenarios, allowing us to systematically consider the influence of various factors (sample size, dimensionality, sparsity, signal strength and multicollinearity). We consider several widely-used methods (Lasso, Elastic Net, Ridge Regression, SCAD, the Dantzig Selector as well as Stability Selection). We find considerable variation in performance between methods, with results dependent on details of the data-generating scenario and the specific goal. Our results support a `no panacea' view, with no unambiguous winner across all scenarios, even in this restricted setting where all data align well with the assumptions underlying the methods. Lasso is well-behaved, performing competitively in many scenarios, while SCAD is highly variable. Substantial benefits from a Ridge-penalty are only seen in the most challenging scenarios with strong multi-collinearity. The results are supported by semi-synthetic analyzes using gene expression data from cancer samples. Our empirical results complement existing theory and provide a resource to compare methods across a range of scenarios and metrics.

Causal Discovery as Semi-Supervised Learning

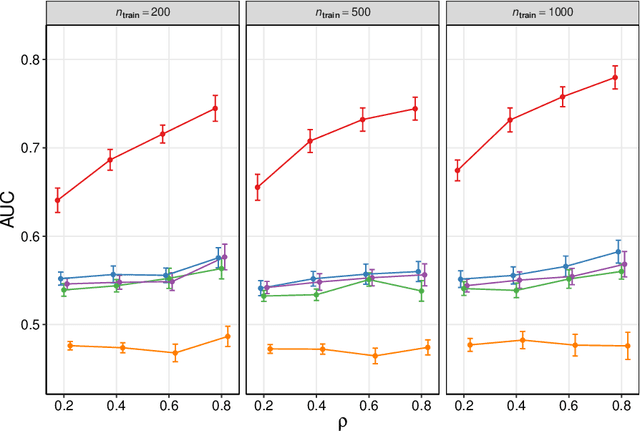
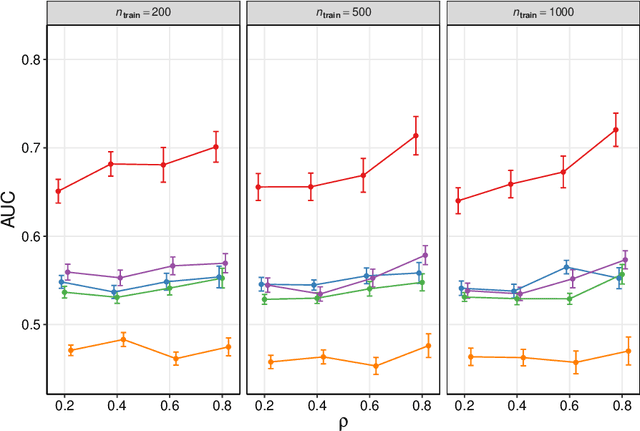
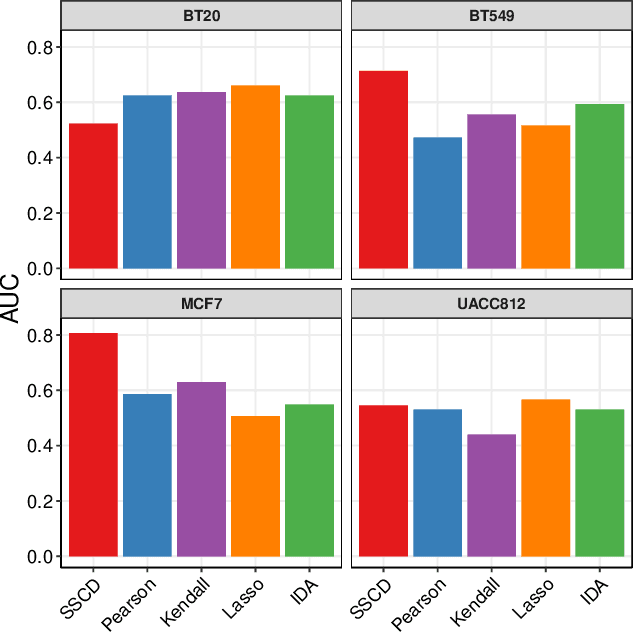
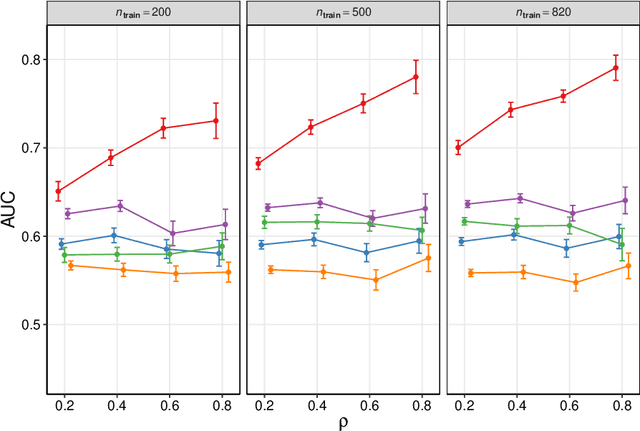
We frame causal discovery as a semi-supervised machine learning task. The idea is to allow direct learning of a causal graph by treating indicators of causal influence between variables as "labels". Available data on the variables of interest are used to provide features for the labelling task. Background knowledge or any available interventional data provide labels on some edges in the graph and the remaining edges are treated as unlabelled. To illustrate the key ideas, we develop a distance-based approach (based on simple bivariate histograms) within a semi-supervised manifold regularization framework. We present empirical results on three different biological datasets (including data where causal effects can be verified by experimental intervention), which demonstrate the efficacy and highly general nature of the approach as well as its simplicity from a user's point of view.

Network-based clustering with mixtures of L1-penalized Gaussian graphical models: an empirical investigation

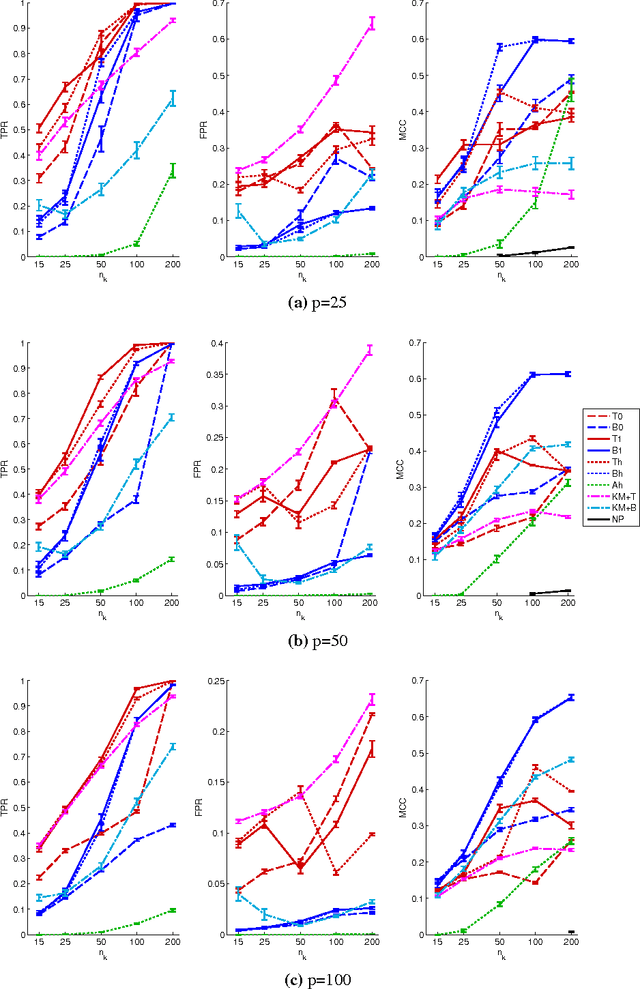
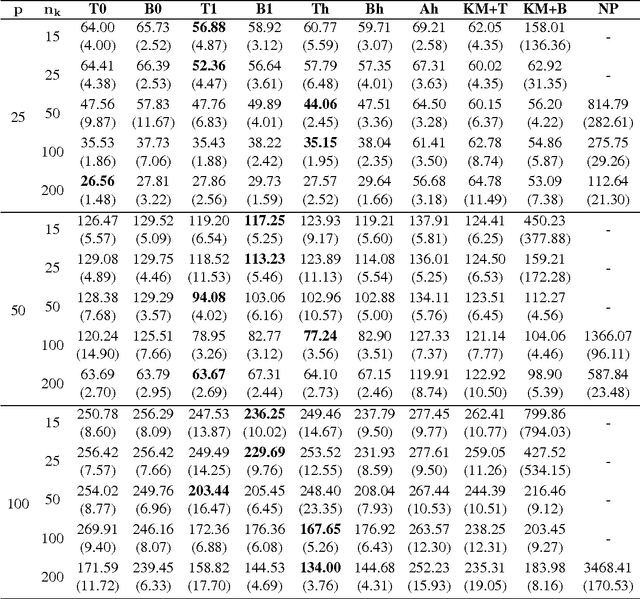
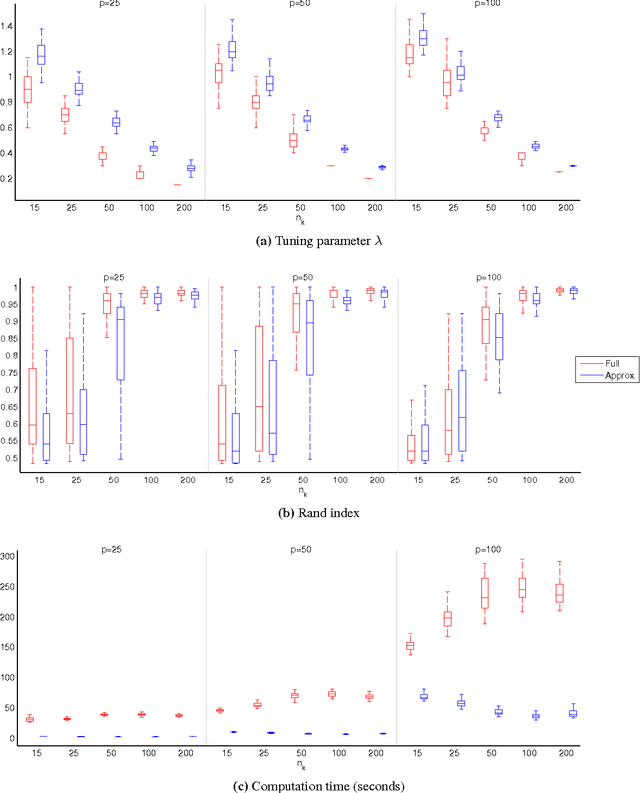
In many applications, multivariate samples may harbor previously unrecognized heterogeneity at the level of conditional independence or network structure. For example, in cancer biology, disease subtypes may differ with respect to subtype-specific interplay between molecular components. Then, both subtype discovery and estimation of subtype-specific networks present important and related challenges. To enable such analyses, we put forward a mixture model whose components are sparse Gaussian graphical models. This brings together model-based clustering and graphical modeling to permit simultaneous estimation of cluster assignments and cluster-specific networks. We carry out estimation within an L1-penalized framework, and investigate several specific penalization regimes. We present empirical results on simulated data and provide general recommendations for the formulation and use of mixtures of L1-penalized Gaussian graphical models.