Network-based clustering with mixtures of L1-penalized Gaussian graphical models: an empirical investigation

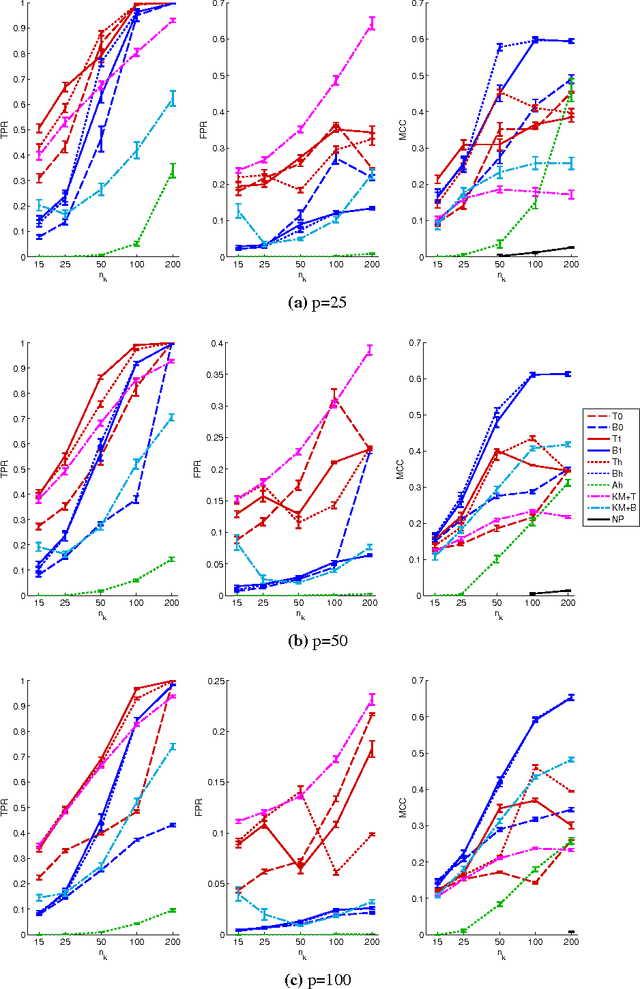
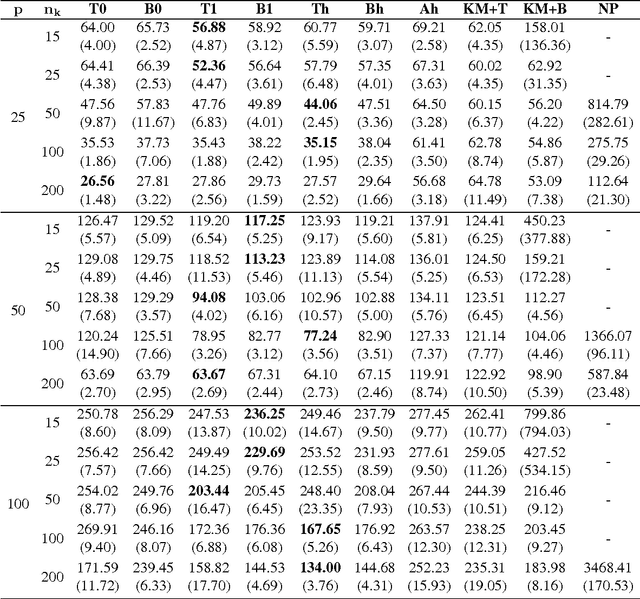
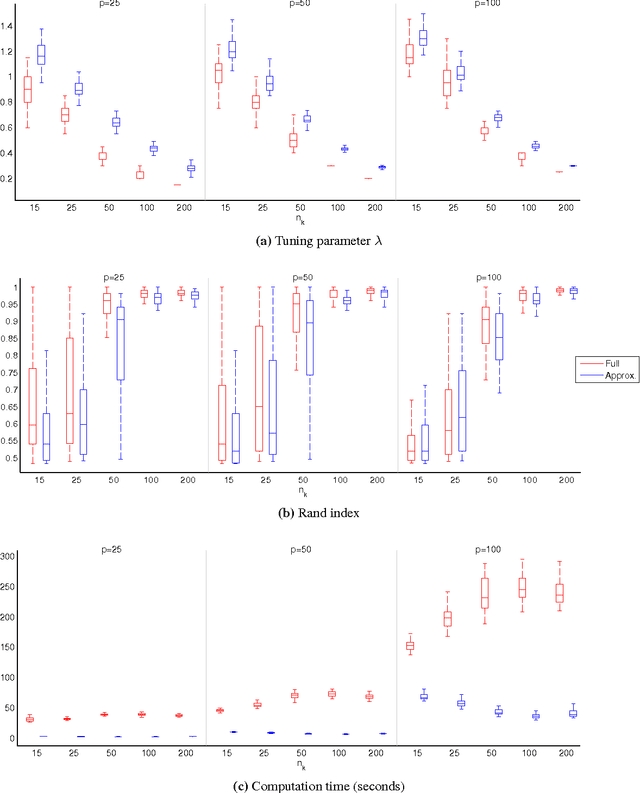
In many applications, multivariate samples may harbor previously unrecognized heterogeneity at the level of conditional independence or network structure. For example, in cancer biology, disease subtypes may differ with respect to subtype-specific interplay between molecular components. Then, both subtype discovery and estimation of subtype-specific networks present important and related challenges. To enable such analyses, we put forward a mixture model whose components are sparse Gaussian graphical models. This brings together model-based clustering and graphical modeling to permit simultaneous estimation of cluster assignments and cluster-specific networks. We carry out estimation within an L1-penalized framework, and investigate several specific penalization regimes. We present empirical results on simulated data and provide general recommendations for the formulation and use of mixtures of L1-penalized Gaussian graphical models.