Chris. J. Oates
Stationary MMD Points for Cubature
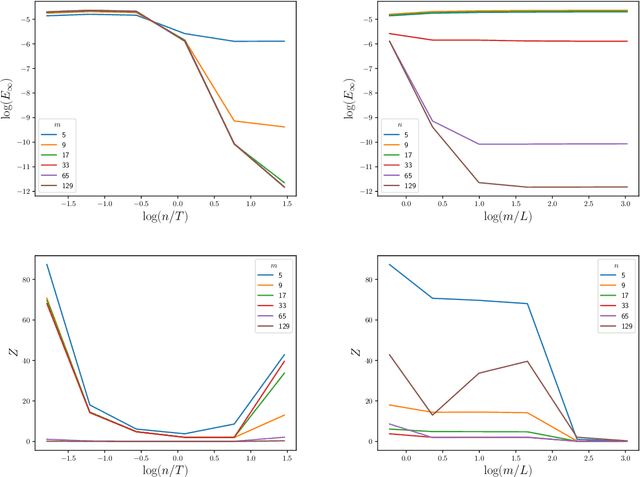
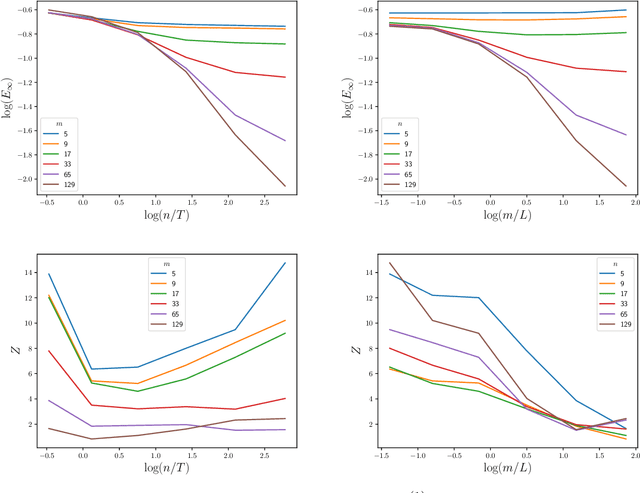
May 27, 2025Abstract:Approximation of a target probability distribution using a finite set of points is a problem of fundamental importance, arising in cubature, data compression, and optimisation. Several authors have proposed to select points by minimising a maximum mean discrepancy (MMD), but the non-convexity of this objective precludes global minimisation in general. Instead, we consider \emph{stationary} points of the MMD which, in contrast to points globally minimising the MMD, can be accurately computed. Our main theoretical contribution is the (perhaps surprising) result that, for integrands in the associated reproducing kernel Hilbert space, the cubature error of stationary MMD points vanishes \emph{faster} than the MMD. Motivated by this \emph{super-convergence} property, we consider discretised gradient flows as a practical strategy for computing stationary points of the MMD, presenting a refined convergence analysis that establishes a novel non-asymptotic finite-particle error bound, which may be of independent interest.
Reinforcement Learning for Adaptive MCMC
May 22, 2024



Abstract:An informal observation, made by several authors, is that the adaptive design of a Markov transition kernel has the flavour of a reinforcement learning task. Yet, to-date it has remained unclear how to actually exploit modern reinforcement learning technologies for adaptive MCMC. The aim of this paper is to set out a general framework, called Reinforcement Learning Metropolis--Hastings, that is theoretically supported and empirically validated. Our principal focus is on learning fast-mixing Metropolis--Hastings transition kernels, which we cast as deterministic policies and optimise via a policy gradient. Control of the learning rate provably ensures conditions for ergodicity are satisfied. The methodology is used to construct a gradient-free sampler that out-performs a popular gradient-free adaptive Metropolis--Hastings algorithm on $\approx 90 \%$ of tasks in the PosteriorDB benchmark.
Sobolev Spaces, Kernels and Discrepancies over Hyperspheres
Nov 16, 2022Abstract:This work provides theoretical foundations for kernel methods in the hyperspherical context. Specifically, we characterise the native spaces (reproducing kernel Hilbert spaces) and the Sobolev spaces associated with kernels defined over hyperspheres. Our results have direct consequences for kernel cubature, determining the rate of convergence of the worst case error, and expanding the applicability of cubature algorithms based on Stein's method. We first introduce a suitable characterisation on Sobolev spaces on the $d$-dimensional hypersphere embedded in $(d+1)$-dimensional Euclidean spaces. Our characterisation is based on the Fourier--Schoenberg sequences associated with a given kernel. Such sequences are hard (if not impossible) to compute analytically on $d$-dimensional spheres, but often feasible over Hilbert spheres. We circumvent this problem by finding a projection operator that allows to Fourier mapping from Hilbert into finite dimensional hyperspheres. We illustrate our findings through some parametric families of kernels.
Generalised Bayesian Inference for Discrete Intractable Likelihood
Jun 16, 2022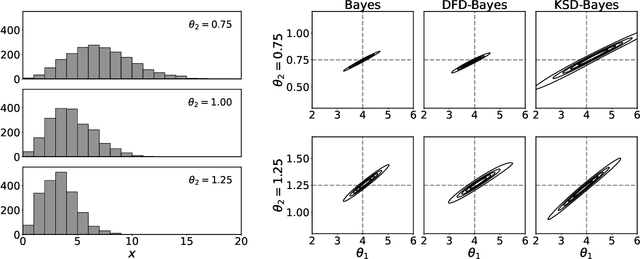
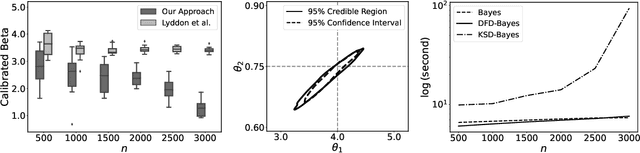
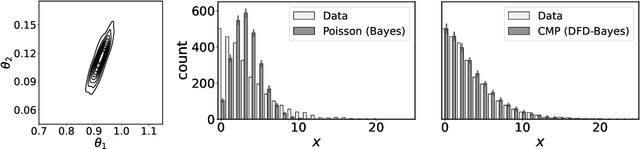
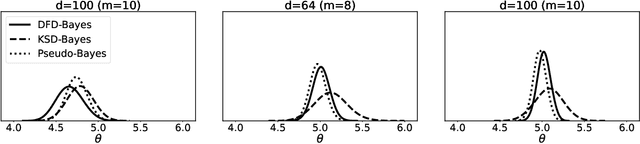
Abstract:Discrete state spaces represent a major computational challenge to statistical inference, since the computation of normalisation constants requires summation over large or possibly infinite sets, which can be impractical. This paper addresses this computational challenge through the development of a novel generalised Bayesian inference procedure suitable for discrete intractable likelihood. Inspired by recent methodological advances for continuous data, the main idea is to update beliefs about model parameters using a discrete Fisher divergence, in lieu of the problematic intractable likelihood. The result is a generalised posterior that can be sampled using standard computational tools, such as Markov chain Monte Carlo, circumventing the intractable normalising constant. The statistical properties of the generalised posterior are analysed, with sufficient conditions for posterior consistency and asymptotic normality established. In addition, a novel and general approach to calibration of generalised posteriors is proposed. Applications are presented on lattice models for discrete spatial data and on multivariate models for count data, where in each case the methodology facilitates generalised Bayesian inference at low computational cost.
Black Box Probabilistic Numerics
Jun 15, 2021

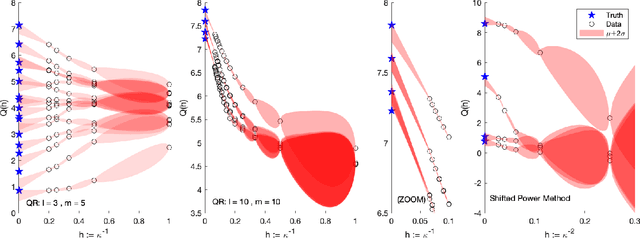
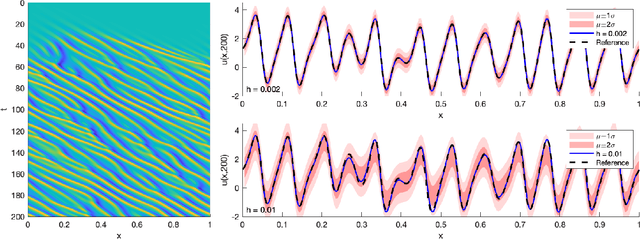
Abstract:Probabilistic numerics casts numerical tasks, such the numerical solution of differential equations, as inference problems to be solved. One approach is to model the unknown quantity of interest as a random variable, and to constrain this variable using data generated during the course of a traditional numerical method. However, data may be nonlinearly related to the quantity of interest, rendering the proper conditioning of random variables difficult and limiting the range of numerical tasks that can be addressed. Instead, this paper proposes to construct probabilistic numerical methods based only on the final output from a traditional method. A convergent sequence of approximations to the quantity of interest constitute a dataset, from which the limiting quantity of interest can be extrapolated, in a probabilistic analogue of Richardson's deferred approach to the limit. This black box approach (1) massively expands the range of tasks to which probabilistic numerics can be applied, (2) inherits the features and performance of state-of-the-art numerical methods, and (3) enables provably higher orders of convergence to be achieved. Applications are presented for nonlinear ordinary and partial differential equations, as well as for eigenvalue problems-a setting for which no probabilistic numerical methods have yet been developed.
Bayesian Numerical Methods for Nonlinear Partial Differential Equations
May 03, 2021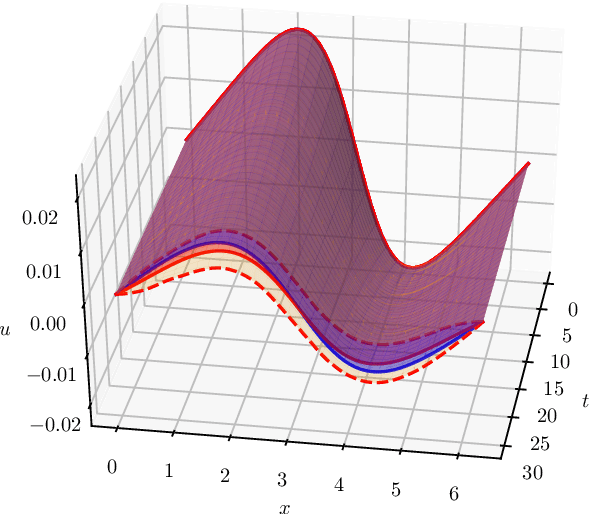
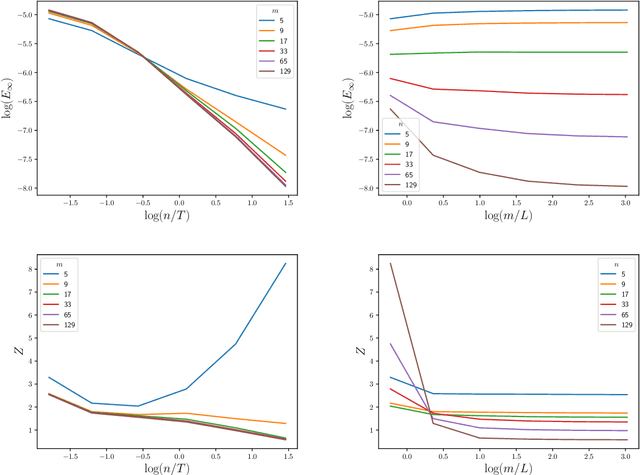
Abstract:The numerical solution of differential equations can be formulated as an inference problem to which formal statistical approaches can be applied. However, nonlinear partial differential equations (PDEs) pose substantial challenges from an inferential perspective, most notably the absence of explicit conditioning formula. This paper extends earlier work on linear PDEs to a general class of initial value problems specified by nonlinear PDEs, motivated by problems for which evaluations of the right-hand-side, initial conditions, or boundary conditions of the PDE have a high computational cost. The proposed method can be viewed as exact Bayesian inference under an approximate likelihood, which is based on discretisation of the nonlinear differential operator. Proof-of-concept experimental results demonstrate that meaningful probabilistic uncertainty quantification for the unknown solution of the PDE can be performed, while controlling the number of times the right-hand-side, initial and boundary conditions are evaluated. A suitable prior model for the solution of the PDE is identified using novel theoretical analysis of the sample path properties of Mat\'{e}rn processes, which may be of independent interest.
Robust Generalised Bayesian Inference for Intractable Likelihoods
Apr 15, 2021



Abstract:Generalised Bayesian inference updates prior beliefs using a loss function, rather than a likelihood, and can therefore be used to confer robustness against possible misspecification of the likelihood. Here we consider generalised Bayesian inference with a Stein discrepancy as a loss function, motivated by applications in which the likelihood contains an intractable normalisation constant. In this context, the Stein discrepancy circumvents evaluation of the normalisation constant and produces generalised posteriors that are either closed form or accessible using standard Markov chain Monte Carlo. On a theoretical level, we show consistency, asymptotic normality, and bias-robustness of the generalised posterior, highlighting how these properties are impacted by the choice of Stein discrepancy. Then, we provide numerical experiments on a range of intractable distributions, including applications to kernel-based exponential family models and non-Gaussian graphical models.
Optimal quantisation of probability measures using maximum mean discrepancy
Nov 03, 2020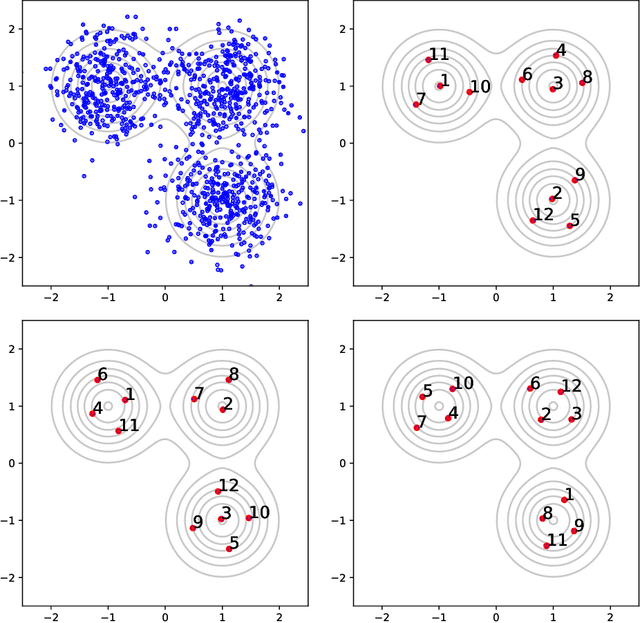
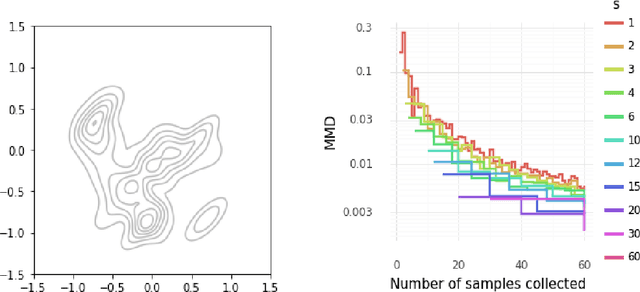
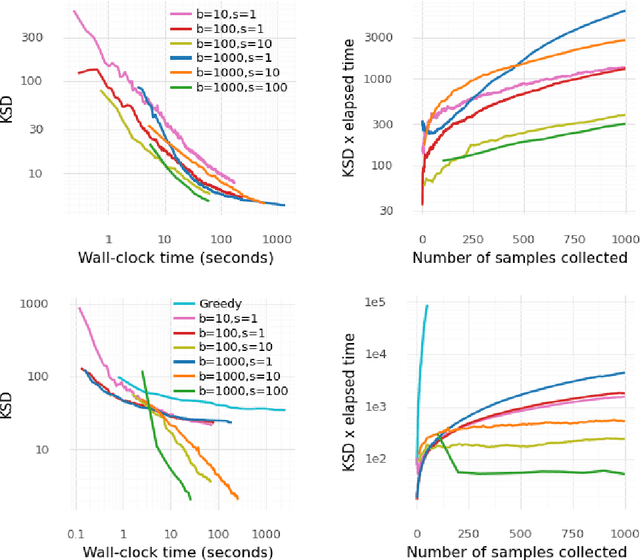
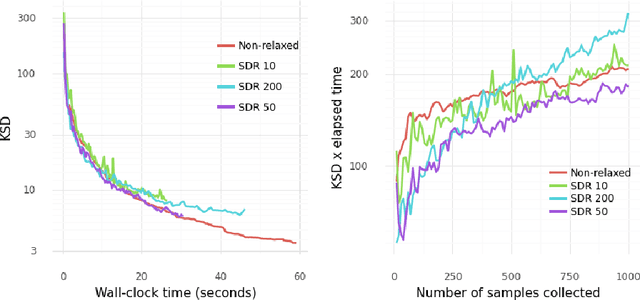
Abstract:Several researchers have proposed minimisation of maximum mean discrepancy (MMD) as a method to quantise probability measures, i.e., to approximate a target distribution by a representative point set. Here we consider sequential algorithms that greedily minimise MMD over a discrete candidate set. We propose a novel non-myopic algorithm and, in order to both improve statistical efficiency and reduce computational cost, we investigate a variant that applies this technique to a mini-batch of the candidate set at each iteration. When the candidate points are sampled from the target, the consistency of these new algorithm - and their mini-batch variants - is established. We demonstrate the algorithms on a range of important computational problems, including optimisation of nodes in Bayesian cubature and the thinning of Markov chain output.
Scalable Control Variates for Monte Carlo Methods via Stochastic Optimization
Jun 12, 2020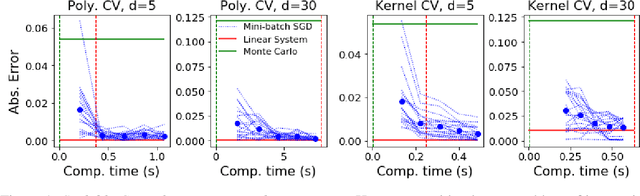
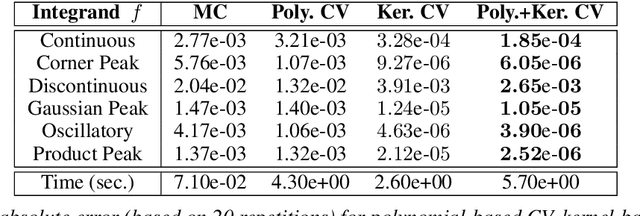
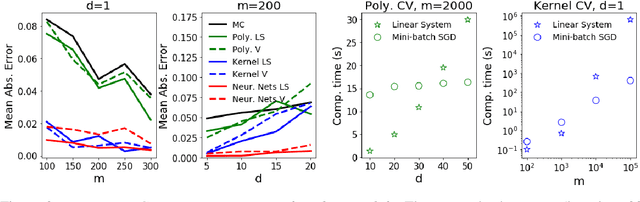
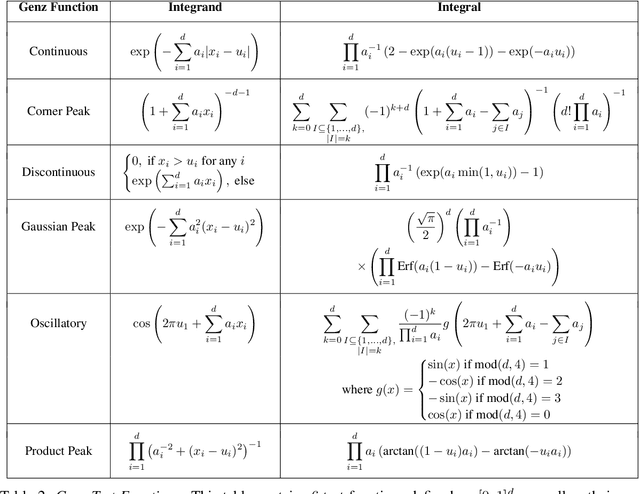
Abstract:Control variates are a well-established tool to reduce the variance of Monte Carlo estimators. However, for large-scale problems including high-dimensional and large-sample settings, their advantages can be outweighed by a substantial computational cost. This paper considers control variates based on Stein operators, presenting a framework that encompasses and generalizes existing approaches that use polynomials, kernels and neural networks. A learning strategy based on minimising a variational objective through stochastic optimization is proposed, leading to scalable and effective control variates. Our results are both empirical, based on a range of test functions and problems in Bayesian inference, and theoretical, based on an analysis of the variance reduction that can be achieved.
Optimal Thinning of MCMC Output
May 08, 2020



Abstract:The use of heuristics to assess the convergence and compress the output of Markov chain Monte Carlo can be sub-optimal in terms of the empirical approximations that are produced. Typically a number of the initial states are attributed to "burn in" and removed, whilst the chain can be "thinned" if compression is also required. In this paper we consider the problem of selecting a subset of states, of fixed cardinality, such that the approximation provided by their empirical distribution is close to optimal. A novel method is proposed, based on greedy minimisation of a kernel Stein discrepancy, that is suitable for problems where heavy compression is required. Theoretical results guarantee consistency of the method and its effectiveness is demonstrated in the challenging context of parameter inference for ordinary differential equations. Software is available in the "Stein Thinning" package in both Python and MATLAB, and example code is included.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge