Optimal quantisation of probability measures using maximum mean discrepancy

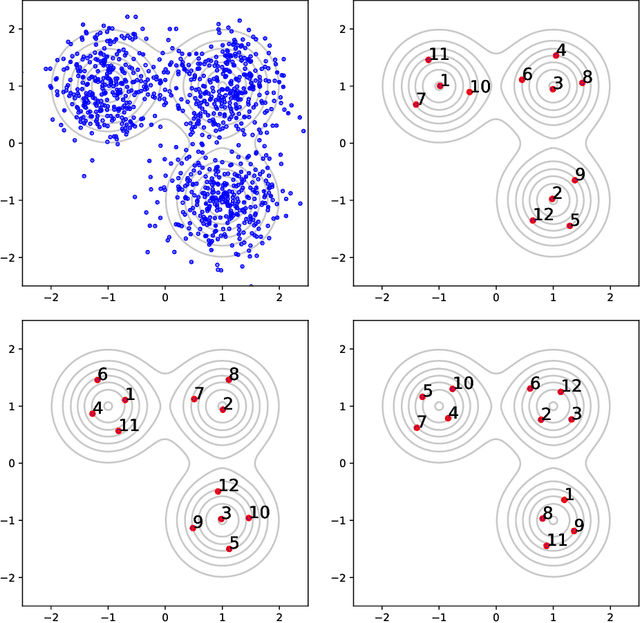
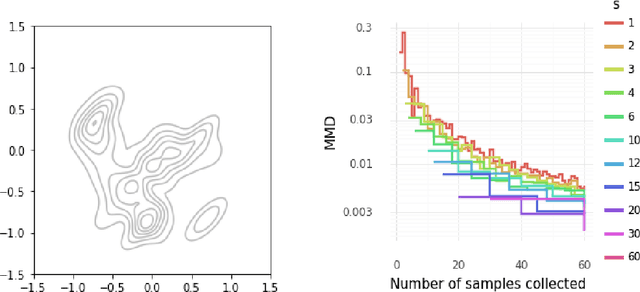
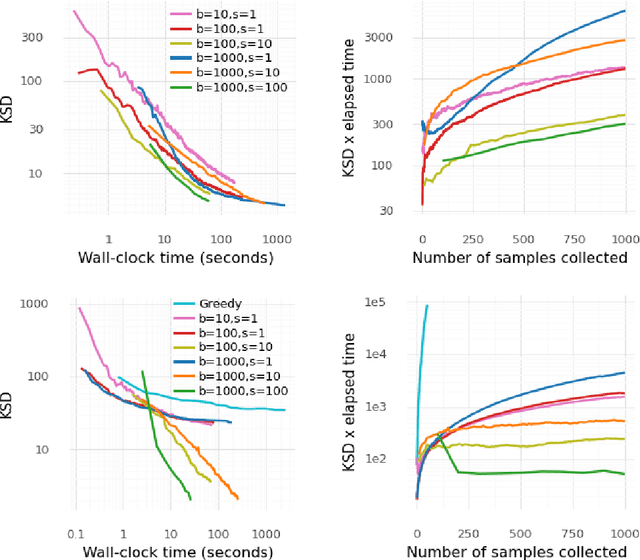
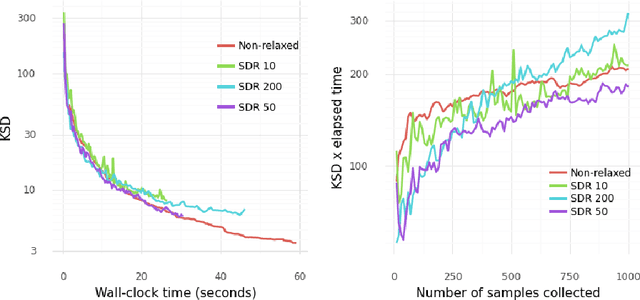
Several researchers have proposed minimisation of maximum mean discrepancy (MMD) as a method to quantise probability measures, i.e., to approximate a target distribution by a representative point set. Here we consider sequential algorithms that greedily minimise MMD over a discrete candidate set. We propose a novel non-myopic algorithm and, in order to both improve statistical efficiency and reduce computational cost, we investigate a variant that applies this technique to a mini-batch of the candidate set at each iteration. When the candidate points are sampled from the target, the consistency of these new algorithm - and their mini-batch variants - is established. We demonstrate the algorithms on a range of important computational problems, including optimisation of nodes in Bayesian cubature and the thinning of Markov chain output.

Stochastic Stein Discrepancies

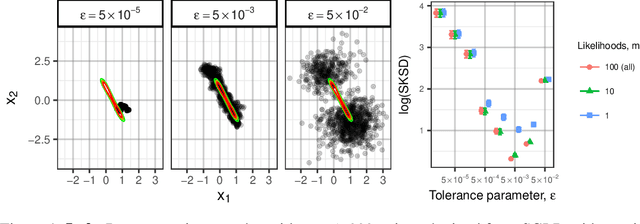
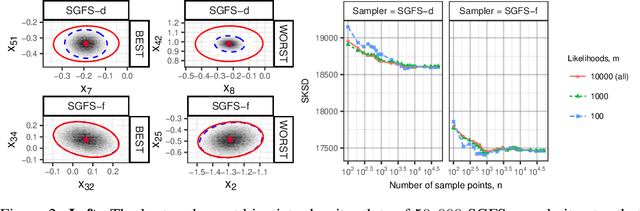
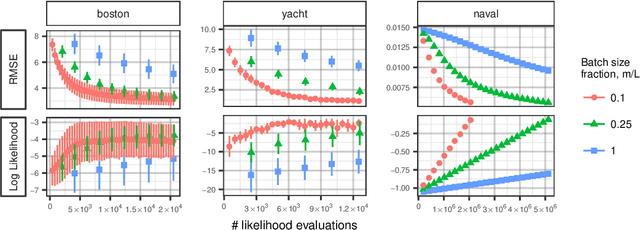
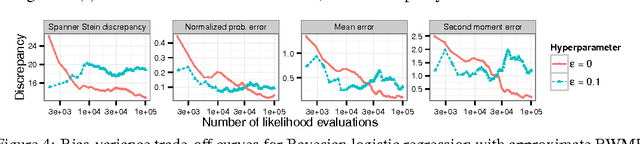
Stein discrepancies (SDs) monitor convergence and non-convergence in approximate inference when exact integration and sampling are intractable. However, the computation of a Stein discrepancy can be prohibitive if the Stein operator - often a sum over likelihood terms or potentials - is expensive to evaluate. To address this deficiency, we show that stochastic Stein discrepancies (SSDs) based on subsampled approximations of the Stein operator inherit the convergence control properties of standard SDs with probability 1. In our experiments with biased Markov chain Monte Carlo (MCMC) hyperparameter tuning, approximate MCMC sampler selection, and stochastic Stein variational gradient descent, SSDs deliver comparable inferences to standard SDs with orders of magnitude fewer likelihood evaluations.

Stein Point Markov Chain Monte Carlo

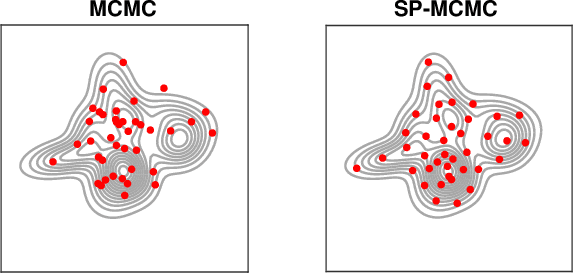
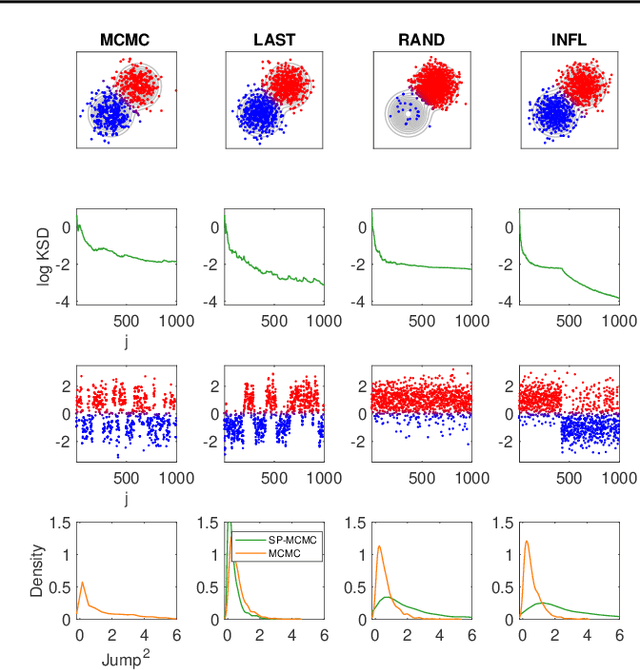
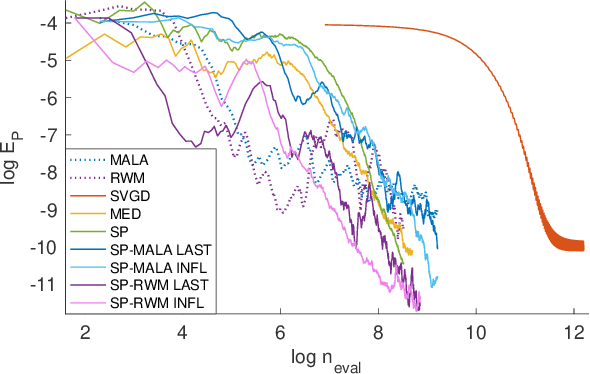
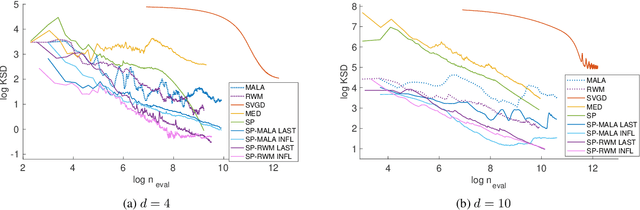
An important task in machine learning and statistics is the approximation of a probability measure by an empirical measure supported on a discrete point set. Stein Points are a class of algorithms for this task, which proceed by sequentially minimising a Stein discrepancy between the empirical measure and the target and, hence, require the solution of a non-convex optimisation problem to obtain each new point. This paper removes the need to solve this optimisation problem by, instead, selecting each new point based on a Markov chain sample path. This significantly reduces the computational cost of Stein Points and leads to a suite of algorithms that are straightforward to implement. The new algorithms are illustrated on a set of challenging Bayesian inference problems, and rigorous theoretical guarantees of consistency are established.

Stein Points

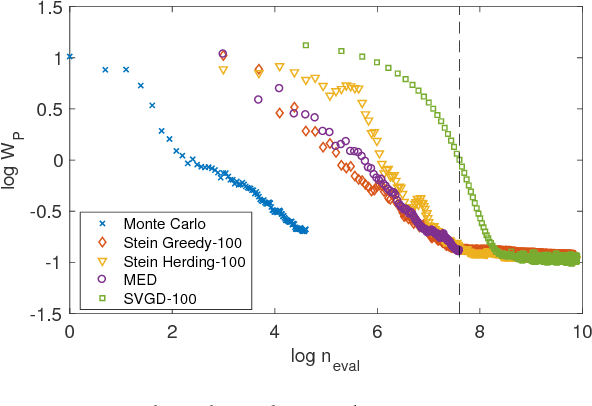
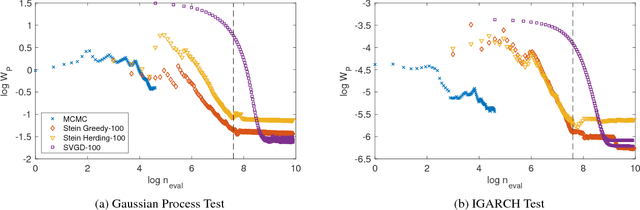
An important task in computational statistics and machine learning is to approximate a posterior distribution $p(x)$ with an empirical measure supported on a set of representative points $\{x_i\}_{i=1}^n$. This paper focuses on methods where the selection of points is essentially deterministic, with an emphasis on achieving accurate approximation when $n$ is small. To this end, we present `Stein Points'. The idea is to exploit either a greedy or a conditional gradient method to iteratively minimise a kernel Stein discrepancy between the empirical measure and $p(x)$. Our empirical results demonstrate that Stein Points enable accurate approximation of the posterior at modest computational cost. In addition, theoretical results are provided to establish convergence of the method.

Measuring Sample Quality with Diffusions

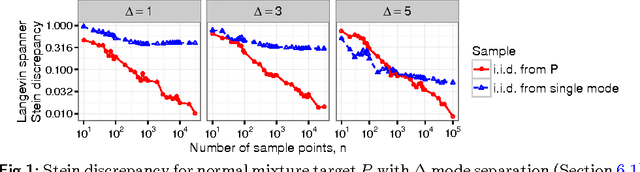
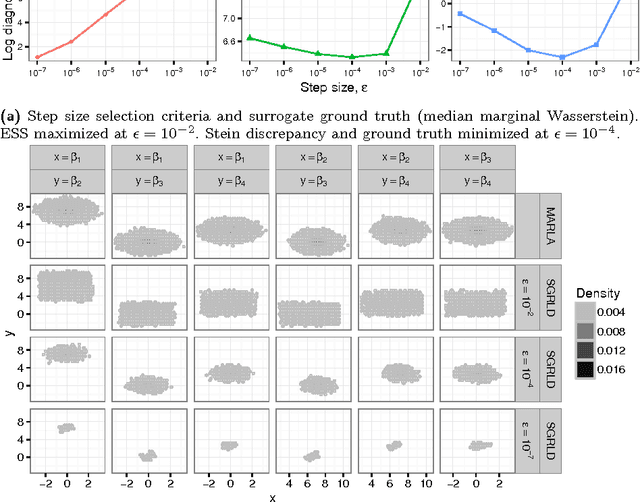
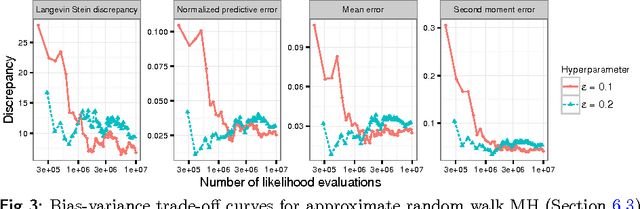
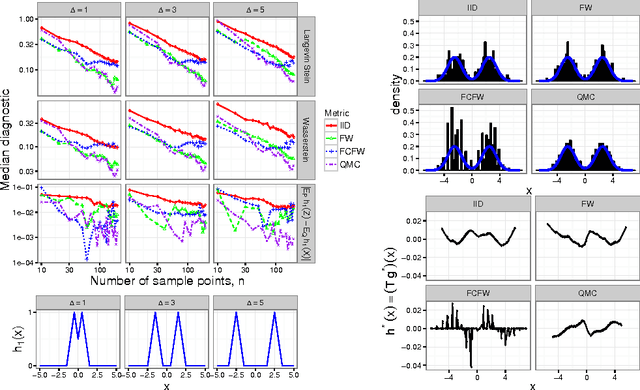
Stein's method for measuring convergence to a continuous target distribution relies on an operator characterizing the target and Stein factor bounds on the solutions of an associated differential equation. While such operators and bounds are readily available for a diversity of univariate targets, few multivariate targets have been analyzed. We introduce a new class of characterizing operators based on Ito diffusions and develop explicit multivariate Stein factor bounds for any target with a fast-coupling Ito diffusion. As example applications, we develop computable and convergence-determining diffusion Stein discrepancies for log-concave, heavy-tailed, and multimodal targets and use these quality measures to select the hyperparameters of biased Markov chain Monte Carlo (MCMC) samplers, compare random and deterministic quadrature rules, and quantify bias-variance tradeoffs in approximate MCMC. Our results establish a near-linear relationship between diffusion Stein discrepancies and Wasserstein distances, improving upon past work even for strongly log-concave targets. The exposed relationship between Stein factors and Markov process coupling may be of independent interest.

Measuring Sample Quality with Kernels

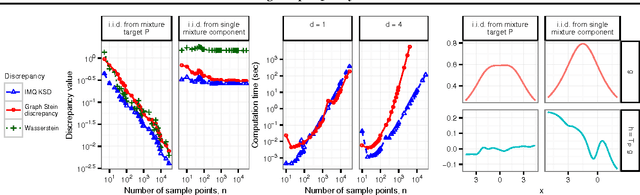
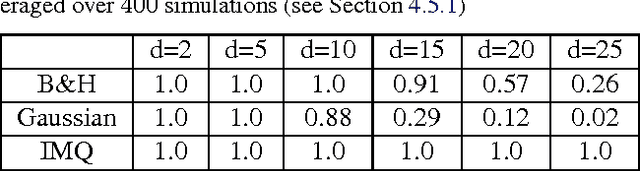
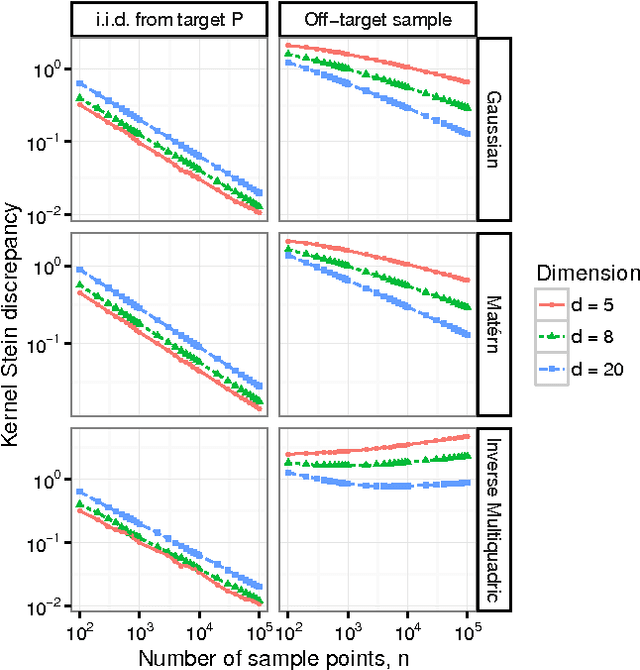
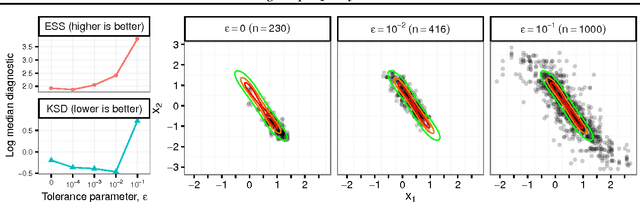
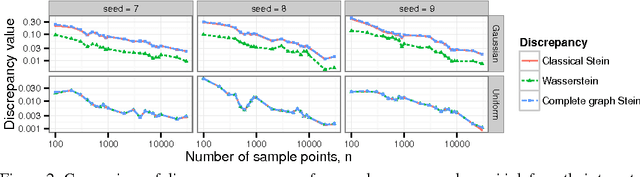
Approximate Markov chain Monte Carlo (MCMC) offers the promise of more rapid sampling at the cost of more biased inference. Since standard MCMC diagnostics fail to detect these biases, researchers have developed computable Stein discrepancy measures that provably determine the convergence of a sample to its target distribution. This approach was recently combined with the theory of reproducing kernels to define a closed-form kernel Stein discrepancy (KSD) computable by summing kernel evaluations across pairs of sample points. We develop a theory of weak convergence for KSDs based on Stein's method, demonstrate that commonly used KSDs fail to detect non-convergence even for Gaussian targets, and show that kernels with slowly decaying tails provably determine convergence for a large class of target distributions. The resulting convergence-determining KSDs are suitable for comparing biased, exact, and deterministic sample sequences and simpler to compute and parallelize than alternative Stein discrepancies. We use our tools to compare biased samplers, select sampler hyperparameters, and improve upon existing KSD approaches to one-sample hypothesis testing and sample quality improvement.

Measuring Sample Quality with Stein's Method

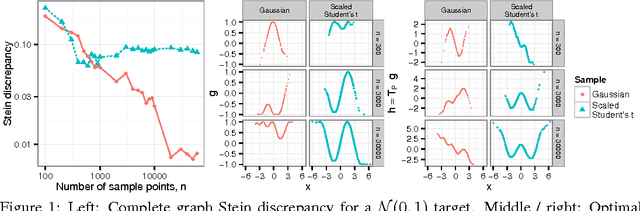
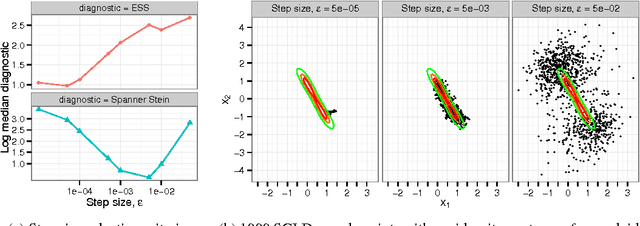
To improve the efficiency of Monte Carlo estimation, practitioners are turning to biased Markov chain Monte Carlo procedures that trade off asymptotic exactness for computational speed. The reasoning is sound: a reduction in variance due to more rapid sampling can outweigh the bias introduced. However, the inexactness creates new challenges for sampler and parameter selection, since standard measures of sample quality like effective sample size do not account for asymptotic bias. To address these challenges, we introduce a new computable quality measure based on Stein's method that quantifies the maximum discrepancy between sample and target expectations over a large class of test functions. We use our tool to compare exact, biased, and deterministic sample sequences and illustrate applications to hyperparameter selection, convergence rate assessment, and quantifying bias-variance tradeoffs in posterior inference.

Computational topology for configuration spaces of hard disks

We explore the topology of configuration spaces of hard disks experimentally, and show that several changes in the topology can already be observed with a small number of particles. The results illustrate a theorem of Baryshnikov, Bubenik, and Kahle that critical points correspond to configurations of disks with balanced mechanical stresses, and suggest conjectures about the asymptotic topology as the number of disks tends to infinity.