Black Box Probabilistic Numerics

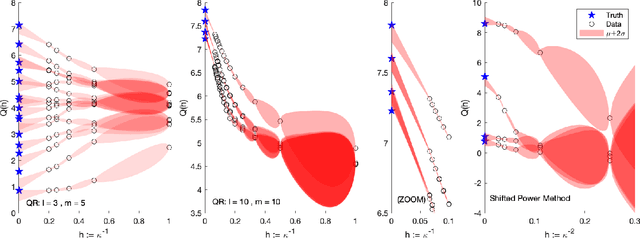
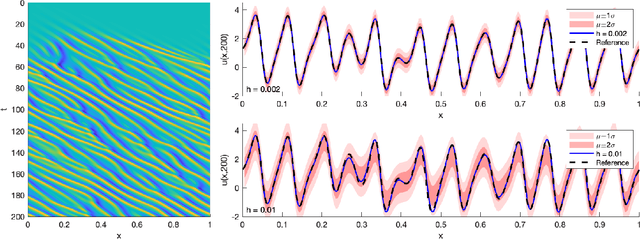
Probabilistic numerics casts numerical tasks, such the numerical solution of differential equations, as inference problems to be solved. One approach is to model the unknown quantity of interest as a random variable, and to constrain this variable using data generated during the course of a traditional numerical method. However, data may be nonlinearly related to the quantity of interest, rendering the proper conditioning of random variables difficult and limiting the range of numerical tasks that can be addressed. Instead, this paper proposes to construct probabilistic numerical methods based only on the final output from a traditional method. A convergent sequence of approximations to the quantity of interest constitute a dataset, from which the limiting quantity of interest can be extrapolated, in a probabilistic analogue of Richardson's deferred approach to the limit. This black box approach (1) massively expands the range of tasks to which probabilistic numerics can be applied, (2) inherits the features and performance of state-of-the-art numerical methods, and (3) enables provably higher orders of convergence to be achieved. Applications are presented for nonlinear ordinary and partial differential equations, as well as for eigenvalue problems-a setting for which no probabilistic numerical methods have yet been developed.

Optimal quantisation of probability measures using maximum mean discrepancy

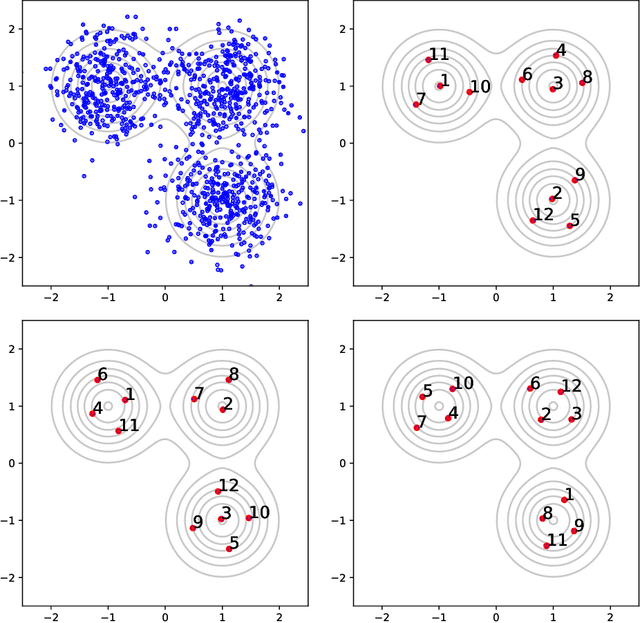
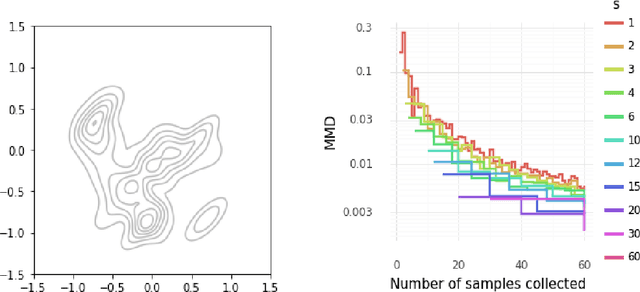
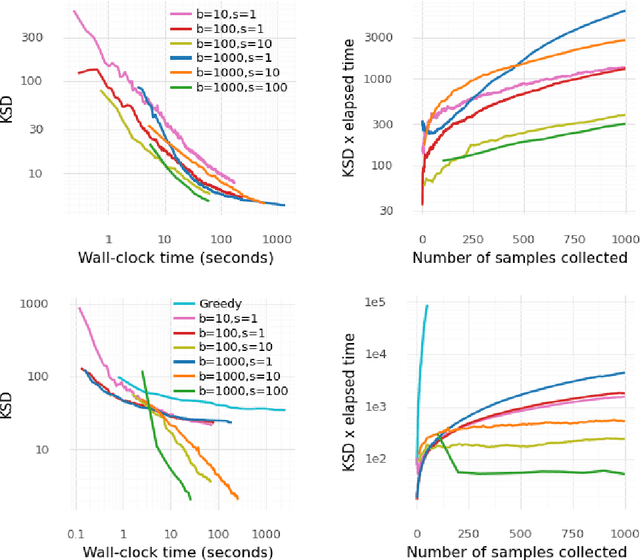
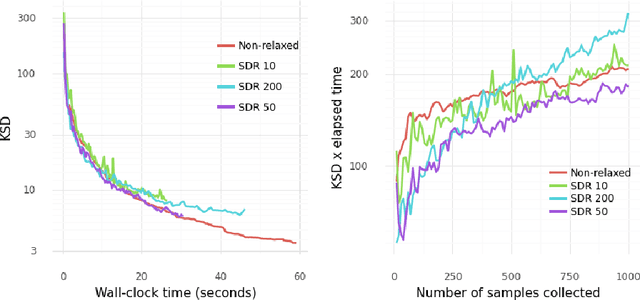
Several researchers have proposed minimisation of maximum mean discrepancy (MMD) as a method to quantise probability measures, i.e., to approximate a target distribution by a representative point set. Here we consider sequential algorithms that greedily minimise MMD over a discrete candidate set. We propose a novel non-myopic algorithm and, in order to both improve statistical efficiency and reduce computational cost, we investigate a variant that applies this technique to a mini-batch of the candidate set at each iteration. When the candidate points are sampled from the target, the consistency of these new algorithm - and their mini-batch variants - is established. We demonstrate the algorithms on a range of important computational problems, including optimisation of nodes in Bayesian cubature and the thinning of Markov chain output.

A Bayesian nonparametric test for conditional independence

This article introduces a Bayesian nonparametric method for quantifying the relative evidence in a dataset in favour of the dependence or independence of two variables conditional on a third. The approach uses Polya tree priors on spaces of conditional probability densities, accounting for uncertainty in the form of the underlying distributions in a nonparametric way. The Bayesian perspective provides an inherently symmetric probability measure of conditional dependence or independence, a feature particularly advantageous in causal discovery and not employed by any previous procedure of this type.

Probabilistic Linear Multistep Methods

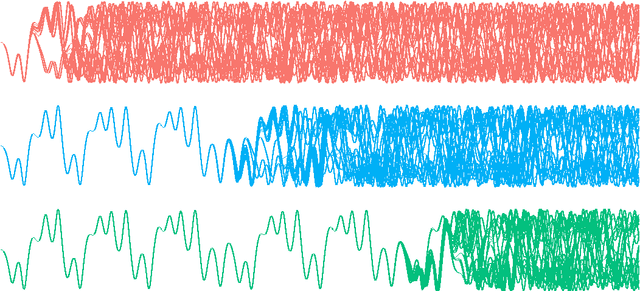
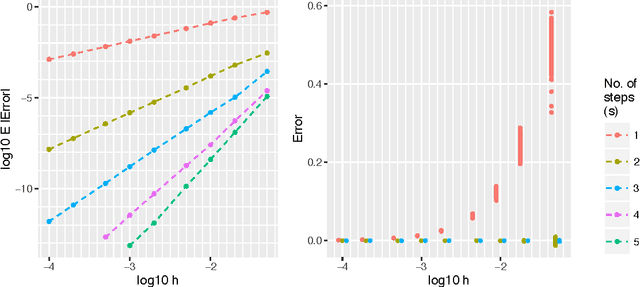
We present a derivation and theoretical investigation of the Adams-Bashforth and Adams-Moulton family of linear multistep methods for solving ordinary differential equations, starting from a Gaussian process (GP) framework. In the limit, this formulation coincides with the classical deterministic methods, which have been used as higher-order initial value problem solvers for over a century. Furthermore, the natural probabilistic framework provided by the GP formulation allows us to derive probabilistic versions of these methods, in the spirit of a number of other probabilistic ODE solvers presented in the recent literature. In contrast to higher-order Runge-Kutta methods, which require multiple intermediate function evaluations per step, Adams family methods make use of previous function evaluations, so that increased accuracy arising from a higher-order multistep approach comes at very little additional computational cost. We show that through a careful choice of covariance function for the GP, the posterior mean and standard deviation over the numerical solution can be made to exactly coincide with the value given by the deterministic method and its local truncation error respectively. We provide a rigorous proof of the convergence of these new methods, as well as an empirical investigation (up to fifth order) demonstrating their convergence rates in practice.