Black Box Probabilistic Numerics

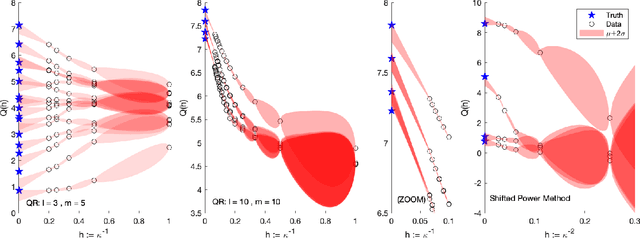
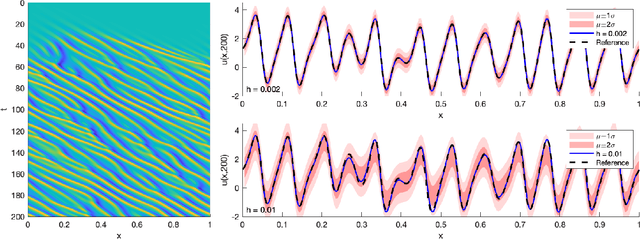
Probabilistic numerics casts numerical tasks, such the numerical solution of differential equations, as inference problems to be solved. One approach is to model the unknown quantity of interest as a random variable, and to constrain this variable using data generated during the course of a traditional numerical method. However, data may be nonlinearly related to the quantity of interest, rendering the proper conditioning of random variables difficult and limiting the range of numerical tasks that can be addressed. Instead, this paper proposes to construct probabilistic numerical methods based only on the final output from a traditional method. A convergent sequence of approximations to the quantity of interest constitute a dataset, from which the limiting quantity of interest can be extrapolated, in a probabilistic analogue of Richardson's deferred approach to the limit. This black box approach (1) massively expands the range of tasks to which probabilistic numerics can be applied, (2) inherits the features and performance of state-of-the-art numerical methods, and (3) enables provably higher orders of convergence to be achieved. Applications are presented for nonlinear ordinary and partial differential equations, as well as for eigenvalue problems-a setting for which no probabilistic numerical methods have yet been developed.

Newton vs the machine: solving the chaotic three-body problem using deep neural networks

Since its formulation by Sir Isaac Newton, the problem of solving the equations of motion for three bodies under their own gravitational force has remained practically unsolved. Currently, the solution for a given initialization can only be found by performing laborious iterative calculations that have unpredictable and potentially infinite computational cost, due to the system's chaotic nature. We show that an ensemble of solutions obtained using an arbitrarily precise numerical integrator can be used to train a deep artificial neural network (ANN) that, over a bounded time interval, provides accurate solutions at fixed computational cost and up to 100 million times faster than a state-of-the-art solver. Our results provide evidence that, for computationally challenging regions of phase-space, a trained ANN can replace existing numerical solvers, enabling fast and scalable simulations of many-body systems to shed light on outstanding phenomena such as the formation of black-hole binary systems or the origin of the core collapse in dense star clusters.

A Bulirsch-Stoer algorithm using Gaussian processes

In this paper, we treat the problem of evaluating the asymptotic error in a numerical integration scheme as one with inherent uncertainty. Adding to the growing field of probabilistic numerics, we show that Gaussian process regression (GPR) can be embedded into a numerical integration scheme to allow for (i) robust selection of the adaptive step-size parameter and; (ii) uncertainty quantification in predictions of putatively converged numerical solutions. We present two examples of our approach using Richardson's extrapolation technique and the Bulirsch-Stoer algorithm. In scenarios where the error-surface is smooth and bounded, our proposed approach can match the results of the traditional polynomial (parametric) extrapolation methods. In scenarios where the error surface is not well approximated by a finite-order polynomial, e.g. in the vicinity of a pole or in the assessment of a chaotic system, traditional methods can fail, however, the non-parametric GPR approach demonstrates the potential to continue to furnish reasonable solutions in these situations.