A hybrid approach for solving the gravitational N-body problem with Artificial Neural Networks

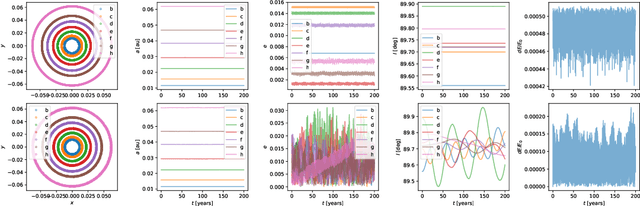
Simulating the evolution of the gravitational N-body problem becomes extremely computationally expensive as N increases since the problem complexity scales quadratically with the number of bodies. We study the use of Artificial Neural Networks (ANNs) to replace expensive parts of the integration of planetary systems. Neural networks that include physical knowledge have grown in popularity in the last few years, although few attempts have been made to use them to speed up the simulation of the motion of celestial bodies. We study the advantages and limitations of using Hamiltonian Neural Networks to replace computationally expensive parts of the numerical simulation. We compare the results of the numerical integration of a planetary system with asteroids with those obtained by a Hamiltonian Neural Network and a conventional Deep Neural Network, with special attention to understanding the challenges of this problem. Due to the non-linear nature of the gravitational equations of motion, errors in the integration propagate. To increase the robustness of a method that uses neural networks, we propose a hybrid integrator that evaluates the prediction of the network and replaces it with the numerical solution if considered inaccurate. Hamiltonian Neural Networks can make predictions that resemble the behavior of symplectic integrators but are challenging to train and in our case fail when the inputs differ ~7 orders of magnitude. In contrast, Deep Neural Networks are easy to train but fail to conserve energy, leading to fast divergence from the reference solution. The hybrid integrator designed to include the neural networks increases the reliability of the method and prevents large energy errors without increasing the computing cost significantly. For this problem, the use of neural networks results in faster simulations when the number of asteroids is >70.

Neural Symplectic Integrator with Hamiltonian Inductive Bias for the Gravitational $N$-body Problem

The gravitational $N$-body problem, which is fundamentally important in astrophysics to predict the motion of $N$ celestial bodies under the mutual gravity of each other, is usually solved numerically because there is no known general analytical solution for $N>2$. Can an $N$-body problem be solved accurately by a neural network (NN)? Can a NN observe long-term conservation of energy and orbital angular momentum? Inspired by Wistom & Holman (1991)'s symplectic map, we present a neural $N$-body integrator for splitting the Hamiltonian into a two-body part, solvable analytically, and an interaction part that we approximate with a NN. Our neural symplectic $N$-body code integrates a general three-body system for $10^{5}$ steps without diverting from the ground truth dynamics obtained from a traditional $N$-body integrator. Moreover, it exhibits good inductive bias by successfully predicting the evolution of $N$-body systems that are no part of the training set.

Newton vs the machine: solving the chaotic three-body problem using deep neural networks

Since its formulation by Sir Isaac Newton, the problem of solving the equations of motion for three bodies under their own gravitational force has remained practically unsolved. Currently, the solution for a given initialization can only be found by performing laborious iterative calculations that have unpredictable and potentially infinite computational cost, due to the system's chaotic nature. We show that an ensemble of solutions obtained using an arbitrarily precise numerical integrator can be used to train a deep artificial neural network (ANN) that, over a bounded time interval, provides accurate solutions at fixed computational cost and up to 100 million times faster than a state-of-the-art solver. Our results provide evidence that, for computationally challenging regions of phase-space, a trained ANN can replace existing numerical solvers, enabling fast and scalable simulations of many-body systems to shed light on outstanding phenomena such as the formation of black-hole binary systems or the origin of the core collapse in dense star clusters.