A hybrid approach for solving the gravitational N-body problem with Artificial Neural Networks

Simulating the evolution of the gravitational N-body problem becomes extremely computationally expensive as N increases since the problem complexity scales quadratically with the number of bodies. We study the use of Artificial Neural Networks (ANNs) to replace expensive parts of the integration of planetary systems. Neural networks that include physical knowledge have grown in popularity in the last few years, although few attempts have been made to use them to speed up the simulation of the motion of celestial bodies. We study the advantages and limitations of using Hamiltonian Neural Networks to replace computationally expensive parts of the numerical simulation. We compare the results of the numerical integration of a planetary system with asteroids with those obtained by a Hamiltonian Neural Network and a conventional Deep Neural Network, with special attention to understanding the challenges of this problem. Due to the non-linear nature of the gravitational equations of motion, errors in the integration propagate. To increase the robustness of a method that uses neural networks, we propose a hybrid integrator that evaluates the prediction of the network and replaces it with the numerical solution if considered inaccurate. Hamiltonian Neural Networks can make predictions that resemble the behavior of symplectic integrators but are challenging to train and in our case fail when the inputs differ ~7 orders of magnitude. In contrast, Deep Neural Networks are easy to train but fail to conserve energy, leading to fast divergence from the reference solution. The hybrid integrator designed to include the neural networks increases the reliability of the method and prevents large energy errors without increasing the computing cost significantly. For this problem, the use of neural networks results in faster simulations when the number of asteroids is >70.

Comparison of neural closure models for discretised PDEs

Neural closure models have recently been proposed as a method for efficiently approximating small scales in multiscale systems with neural networks. The choice of loss function and associated training procedure has a large effect on the accuracy and stability of the resulting neural closure model. In this work, we systematically compare three distinct procedures: "derivative fitting", "trajectory fitting" with discretise-then-optimise, and "trajectory fitting" with optimise-then-discretise. Derivative fitting is conceptually the simplest and computationally the most efficient approach and is found to perform reasonably well on one of the test problems (Kuramoto-Sivashinsky) but poorly on the other (Burgers). Trajectory fitting is computationally more expensive but is more robust and is therefore the preferred approach. Of the two trajectory fitting procedures, the discretise-then-optimise approach produces more accurate models than the optimise-then-discretise approach. While the optimise-then-discretise approach can still produce accurate models, care must be taken in choosing the length of the trajectories used for training, in order to train the models on long-term behaviour while still producing reasonably accurate gradients during training. Two existing theorems are interpreted in a novel way that gives insight into the long-term accuracy of a neural closure model based on how accurate it is in the short term.

On the influence of roundoff errors on the convergence of the gradient descent method with low-precision floating-point computation

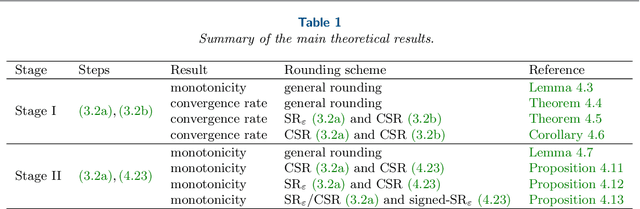
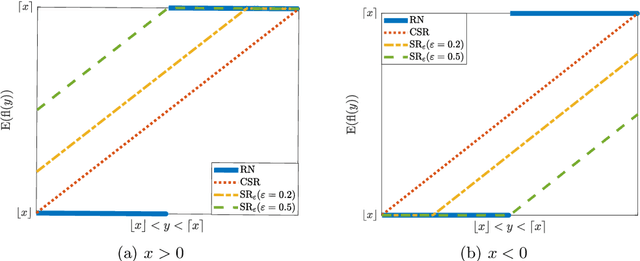
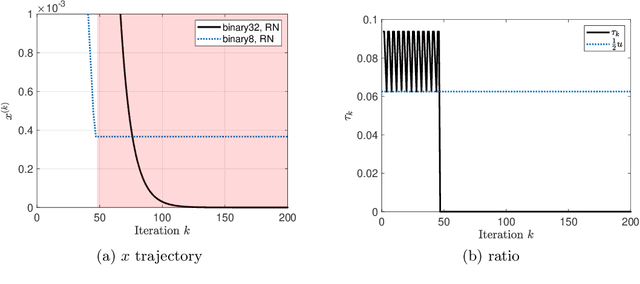
The employment of stochastic rounding schemes helps prevent stagnation of convergence, due to vanishing gradient effect when implementing the gradient descent method in low precision. Conventional stochastic rounding achieves zero bias by preserving small updates with probabilities proportional to their relative magnitudes. In this study, we propose a new stochastic rounding scheme that trades the zero bias property with a larger probability to preserve small gradients. Our method yields a constant rounding bias that, at each iteration, lies in a descent direction. For convex problems, we prove that the proposed rounding method has a beneficial effect on the convergence rate of gradient descent. We validate our theoretical analysis by comparing the performances of various rounding schemes when optimizing a multinomial logistic regression model and when training a simple neural network with 8-bit floating-point format.

A Simple and Efficient Stochastic Rounding Method for Training Neural Networks in Low Precision

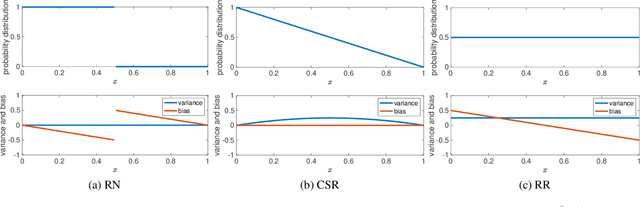
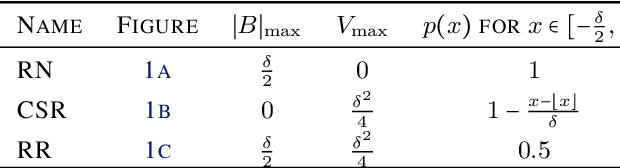
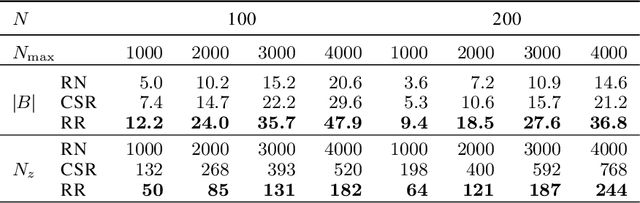
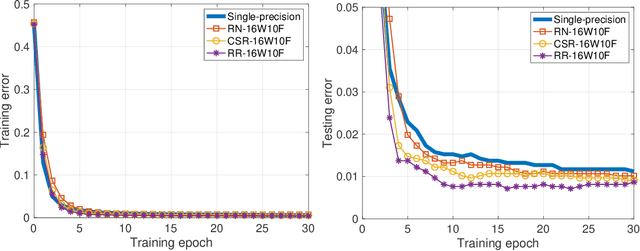
Conventional stochastic rounding (CSR) is widely employed in the training of neural networks (NNs), showing promising training results even in low-precision computations. We introduce an improved stochastic rounding method, that is simple and efficient. The proposed method succeeds in training NNs with 16-bit fixed-point numbers and provides faster convergence and higher classification accuracy than both CSR and deterministic rounding-to-the-nearest method.

Improved stochastic rounding

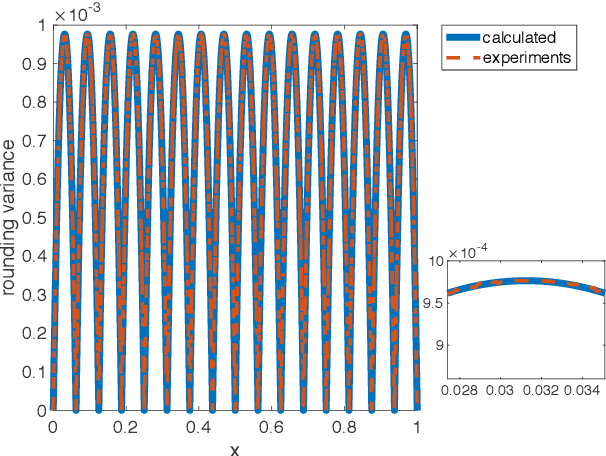
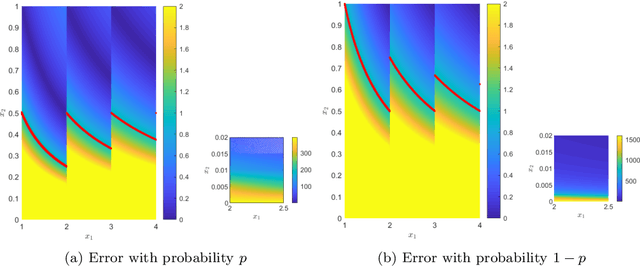
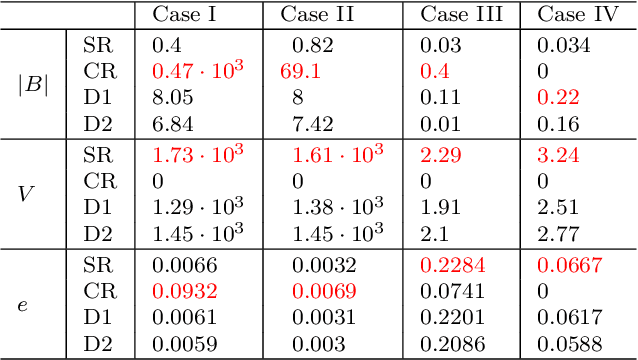
Due to the limited number of bits in floating-point or fixed-point arithmetic, rounding is a necessary step in many computations. Although rounding methods can be tailored for different applications, round-off errors are generally unavoidable. When a sequence of computations is implemented, round-off errors may be magnified or accumulated. The magnification of round-off errors may cause serious failures. Stochastic rounding (SR) was introduced as an unbiased rounding method, which is widely employed in, for instance, the training of neural networks (NNs), showing a promising training result even in low-precision computations. Although the employment of SR in training NNs is consistently increasing, the error analysis of SR is still to be improved. Additionally, the unbiased rounding results of SR are always accompanied by large variances. In this study, some general properties of SR are stated and proven. Furthermore, an upper bound of rounding variance is introduced and validated. Two new probability distributions of SR are proposed to study the trade-off between variance and bias, by solving a multiple objective optimization problem. In the simulation study, the rounding variance, bias, and relative errors of SR are studied for different operations, such as summation, square root calculation through Newton iteration and inner product computation, with specific rounding precision.