Improved stochastic rounding
Paper and Code
May 31, 2020
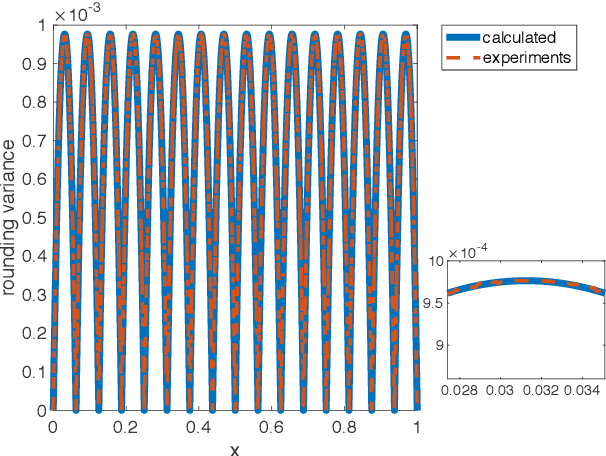
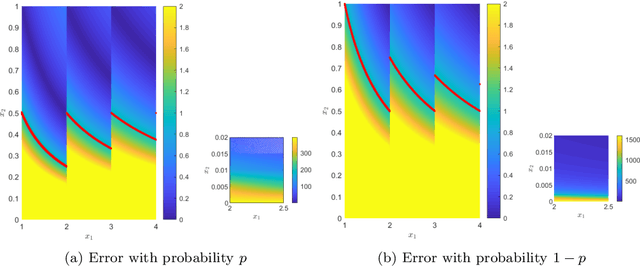
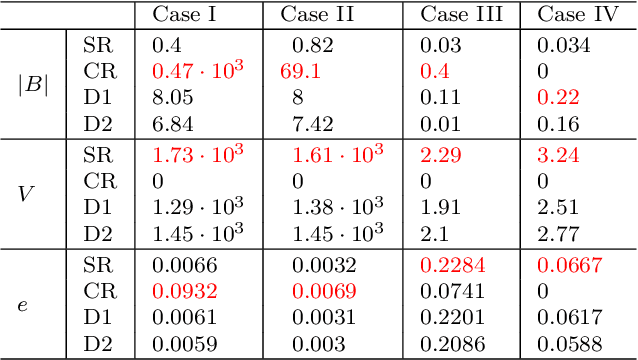
Due to the limited number of bits in floating-point or fixed-point arithmetic, rounding is a necessary step in many computations. Although rounding methods can be tailored for different applications, round-off errors are generally unavoidable. When a sequence of computations is implemented, round-off errors may be magnified or accumulated. The magnification of round-off errors may cause serious failures. Stochastic rounding (SR) was introduced as an unbiased rounding method, which is widely employed in, for instance, the training of neural networks (NNs), showing a promising training result even in low-precision computations. Although the employment of SR in training NNs is consistently increasing, the error analysis of SR is still to be improved. Additionally, the unbiased rounding results of SR are always accompanied by large variances. In this study, some general properties of SR are stated and proven. Furthermore, an upper bound of rounding variance is introduced and validated. Two new probability distributions of SR are proposed to study the trade-off between variance and bias, by solving a multiple objective optimization problem. In the simulation study, the rounding variance, bias, and relative errors of SR are studied for different operations, such as summation, square root calculation through Newton iteration and inner product computation, with specific rounding precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge